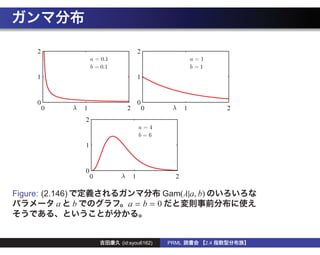
The document discusses probability distributions and their natural parameters. It provides examples of several common distributions including the Bernoulli, multinomial, Gaussian, and gamma distributions. For each distribution, it derives the natural parameter representation and shows how to write the distribution in the form p(x|η) = h(x)g(η)exp{η^T μ(x)}. Maximum likelihood estimation for these distributions is also briefly discussed.

1. PRML 2.4
(id:syou6162)
June 13, 2009
(id:syou6162) PRML 2.4

2. 2.4
2
x η
p(x|η) = h(x)g(η) exp {ηT µ(x)}
x
η (natural parameter) u(x) x
(id:syou6162) PRML 2.4

3. Figure: Figure:
Figure: Figure: t
(id:syou6162) PRML 2.4

4. ?
hoge
←
(id:syou6162) PRML 2.4

5. hoge
( )
η ηML
( )
(id:syou6162) PRML 2.4

6. ∈
(1/2)
: p(x|µ) = Bern(x|µ) = µ x (1 − µ)1−x
→ p(x|η) = h(x)g(η) exp {ηT µ(x)}
p(x|µ) = (1 − µ) exp {log( 1−µ )x}
µ
natural parameter η
η= log( 1−µ )
µ
µ µ = σ(η)
1
σ(η) = 1+exp(−η)
(id:syou6162) PRML 2.4

7. ∈
(2/2)
(2.194)
p(x|η) = σ(−η) exp(ηx)
p(x|η) = h(x)g(η) exp {ηT µ(x)}
η = log( 1−µ )
µ
µ(x) = x
h(x) = 1
g(η) = σ(−η)
(id:syou6162) PRML 2.4

8. ∈
:
M x M
p(x|µ) = k=1 µk k = exp { k=1 xk log µk }
(2.194)
p(x|µ) = exp(ηT x)
ηk = log uk η = (η1 , · · · , ηM )T
p(x|η) = h(x)g(η) exp {ηT µ(x)}
µ(x) = x
h(x) = 1
g(η) = 1
(id:syou6162) PRML 2.4

9. uk (k = 1, · · · , M)
M
k=1 uk =1
→ uk M−1
M−1
(id:syou6162) PRML 2.4

10. M
 
 
exp  xk log uk 

 

 
k=1
 
 M−1 
 
= exp  xk log uk + x M log u M 

 

 
k=1
 
 M−1  M−1 
  M−1

   
= exp  xk log uk + 1 − xk  log 1 −
    
µk  
    
 

 

 

 


k=1 k=1 k=1

 M−1 M−1
 M−1
  M−1

    
= exp  xk log uk − xk log 1 −  + log 1 −
    
µk  µk  
 
   
  
 

 


k=1 k=1 k=1 k=1

 M−1    M−1

 µk  
= exp  xk log   + log 1 −
 
 
  
µk  
  
M−1
 
1 − j=1 µ j
 
 
 

 


k=1 k=1

M−1
   M−1  
   µk 
= 1 − µk  exp  xk log 

 
 
 
 

M−1
 
1 − j=1 µ j 


 

  
 

k=1 k=1

(id:syou6162) PRML 2.4

11. (1/2)
M−1 M−1
1− k=1 µk exp k=1 xk log 1−
µk
M−1
µj
j=1
log 1−
µk
M−1
µj
= ηk
j=1
k
exp(ηk )
µk = 1+ M−1 exp(η j )
j=1
4
(id:syou6162) PRML 2.4

12. (2/2)
M−1 −1
p(x|η) = 1 + j=1 exp(η j ) exp(ηT x)
natural parameter η = (η1 , · · · , ηM−1 )T
p(x|η) = h(x)g(η) exp {ηT µ(x)}
µ(x) = x
h(x) = 1
M−1 −1
g(η) = 1 + j=1 exp(η j )
(id:syou6162) PRML 2.4

13. ∈
:
1
p(x|µ, σ) = 1 exp {− 1 σ2(x − µ)2}
2
(2πσ2 ) 2
(2.194)
1 1 1 2
p(x|µ, σ) = 1 exp {− 2σ2 x2 + µ
σ2
x − 2σ2
µ}
(2πσ2 ) 2
p(x|η) = h(x)g(η) exp {ηT µ(x)}
µ/σ2
η=
−1/2σ2
x
µ(x) =
x2
1
h(x) = (2π)− 2
1 η2
g(η) = (−2η2 ) 2 exp ( 4η12 )
(id:syou6162) PRML 2.4

14. 2.4.1
η
p(x|η) = h(x)g(η) exp {ηT µ(x)}
→ g(η) h(x) exp {ηT u(x)}dx +
g(η) h(x) exp {ηT u(x)}u(x)dx = 0
− log g(η) = E[u(x)]
− log g(η) = cor[u(x)]
(id:syou6162) PRML 2.4

15. & i.i.d.
X = (x1, · · · , xn )
: p(X|η) = L(η; X) =
N N
n=1 h(xn ) g(η)N exp ηT n=1 u(xn )
:
1 N
− g(ηML ) = N n=1 u(xn )
N
n=1 u(xn )
(sufficient
statistic)
(id:syou6162) PRML 2.4

16. u(x) = x
N
n=1 xn
u(x) = (x, x2 )T
N N
( n=1 xn, n=1 x2 )T
n
( )
8
(id:syou6162) PRML 2.4

17. 2.4.2
:
( )
( )
(id:syou6162) PRML 2.4

18. p(η|χ) = f (χ, ν)g(η)ν exp {νηT χ}
= ×
= p(η|χ) × p(X|η)
= f (χ, ν)g(η)ν exp {νηT χ}
 N   N

 g(η)N exp ηT
 
h(xn) u(xn )

 
 
× 
   
  
 
n=1 n=1
 
  N 
 T
  
∝ g(η) µ+N
exp η 
   u(xn) + νχ 


  
n=1

(id:syou6162) PRML 2.4

19. ν
µ(x) χ
(id:syou6162) PRML 2.4

20. 2.4.3
ν
ν
→
(id:syou6162) PRML 2.4

21. 2.4.3
λ K
1
p(λ) = K
x
1
p(x) = b−a
constant
1 1
2
(id:syou6162) PRML 2.4

22. 1:
1
→ (improper prior)
( )
(id:syou6162) PRML 2.4

23. (2.3.6 )
p(µ) = N(µ0 , σ2)
0
→ µ0 = 0
→ σ0 → ∞
→
σ2 Nσ20 σ2 /σ2
0 N
µN = µ
Nσ2 +σ 0
+ µ
Nσ2 +σ ML
= N+σ/σ2 0
µ + µ
N+σ/σ2 ML
→
0 0 0 0
µML
1 1 N N
σ2
= σ2
+ σ2
→ σ2
N 0
(id:syou6162) PRML 2.4

24. (1/2)
h(λ) λ = η2
η = h(η2)
ˆ
pλ (λ) λ = η2
pη (η) = pλ (λ)| dλ | = pλ (η2 )2η ∝ η
dη
pλ (λ) pη (η)
(id:syou6162) PRML 2.4

25. (2/2)
?
(translation invariance)
(scale invariance)
(id:syou6162) PRML 2.4

26. p(x|µ) = f (x − µ)
x x = x+c
ˆ µ =µ+c
ˆ
p(x|µ) = f ( x − µ) = f ((x + c) − (µ + c)) = p( x|µ)
ˆ ˆ ˆˆ
(id:syou6162) PRML 2.4

27. A≤µ≤B
A−c ≤µ≤ B−c
B B−c B
A
p(µ)dµ = p(µ)dµ =
A−c A
p(µ − c)dµ
A B
→ p(µ − c) = p(µ)
p(µ)
?
(id:syou6162) PRML 2.4

28. µ
µ0 = 0
σ2 Nσ20
µN = µ
Nσ2 +σ 0
+ µ
Nσ2 +σ ML
=
0 0
σ2 /σ2
0 N
N+σ/σ2 0
µ + µ
N+σ/σ2 ML
→ µML
0 0
σ2 →
0 ∞
µ
(id:syou6162) PRML 2.4

29. 1 x
σ>0 p(x|σ) = σ f (σ)
x x = cx
ˆ σ = cσ
ˆ
1 x 1 cx 1 cx
p(x|σ) = σ f ( σ ) = σ f ( cσ ) = σ f(σ) =
ˆ
1 x
ˆ 1 x
ˆ
cσ f ( σ ) = σ f ( σ )p( x|σ)
ˆ ˆ ˆ ˆˆ
(id:syou6162) PRML 2.4

30. A≤σ≤B
A/c ≤ µ ≤ B/c
B B/c B
A
p(σ)dσ = p(σ)dσ =
A/c A
p( 1 σ) 1 dσ
c c
A B
→ p(σ) = p( 1 σ) 1
c c
1
p(σ) ∝ σ
? ?
f (x) = 1/x x = 10
f (10/2) × 2 = f (5) × 1 = 0.2 ×
1
2
1
2
= 0.1 = f (10)
1/x
(id:syou6162) PRML 2.4

31. µ
σ
N(x|µ, σ2 ) ∝ σ−1 exp{−( x/σ)2 }
ˆ
x= x−µ
ˆ
λ = 1/σ2
p(σ) ∝ 1/σ p(λ) ∝ 1/λ
3 3
p(λ) = p(σ) × | dσ | = p(σ) × | − λ− 2 /2| ∝ 1/σ × λ− 2 =
dλ
1/2 −3
2 = 1/λ
λ ×λ
√
σ = 1/λ
3
dσ/dλ = −λ− 2 /2
λ (2.146)
Gam(λ|a0 , b0 )
(id:syou6162) PRML 2.4

32. Figure: (2.146) Gam(λ|a, b)
a b a=b=0
(id:syou6162) PRML 2.4

33. a0 = 0 b0 = 0
a N = a0 + N2
N
bN = 1 n=1 (xn − µ)2 = b0 + N σ2
2 2 ML
a0 = 0 b0 = 0
(id:syou6162) PRML 2.4