Let's go through this step-by-step: 1) The log-likelihood function for a Poisson with parameter λ is: l(λ; y) = ylog(λ) - λ - log(y!) 2) Take the derivative of the log-likelihood with respect to λ: ∂l/∂λ = y/λ - 1 3) Set the derivative equal to 0 and solve for λ: y/λ - 1 = 0 y/λ = 1 λ = y Therefore, the MLE for the Poisson parameter λ is simply the observed value y.

1. Chapter 2
The Likelihood Approach
報告者：胡 元

2. 1. Define a hierarchy of models.
2. Express the likelihood functions for
the models.
3. Find the parameters that maximize
the likelihood functions.
4. Compare the values of likelihood to
decide which model is best.

3. 使用的範例
投擲吐司
N為投擲吐司的次數
Random variable Y為奶油面朝下的機
率，y為Y的realization
目標是估計吐司面朝下的機率p

4. 2.1.1 A hierarchy of models
Y ∼ Binomial(N, p)
－只有一個model，故不用說明model的階層性

5. 2.1.2 Express the likelihood function
→以投擲吐司的pmf: Pr(Y = y)為例
 N y
  p (1− p )N − y
, y = 0,..., N
  y
 
f ( y; p ) = 
 , otherwise
 0

6. pmf   N  p y (1− p )N − y , y = 0,..., N
 
 y 
 
f ( y; p ) = 
 , otherwise
 0
Likelihood Function 相同！
N y
L( p; y ) =   p (1 − p )
N−y
 y
 

7. Likelihood Function
N y
L( p; y ) =   p (1 − p )
N−y
 y
 
→ L是參數p的likelihood function

8. Likelihood Function
For a discrete random variable, the likelihood
function is the probability mass function
expressed as a function of the parameters.
- Definition 26

9. 5 successes from 10 flips 50 successes from 100 flips
7 successes from 10 flips 70 successes from 100 flips

10. p=0:.01:1
like1 = bilike(p,5,10) %圖A的binominal likelihood function
like2 = bilike(p,50,100) %圖B的binominal likelihood function
like3 = bilike(p,7,10) %圖C的binominal likelihood function
like4 = bilike(p,70,100) %圖D的binominal likelihood function
plot(p,like1,p,like2,p,like3,p,like4) %畫出圖A~D

11. 5 successes from 10 flips 50 successes from 100 flips
In Panel A, the maximum of the likelihood (about .25)
is far smaller than that in Panel B.
In most applications, the actual value of likelihood is
not important.

12. • 對二項分配來說，likelihood受p和Bernoulli trials
數N所影響。
• 對估計來說，重要的是likelihood function的形狀
和高峰所在的位置（下面有更詳細的討論）。
• 對模型比較來說，likelihood value的不同才重要。

14. 1. Define a hierarchy of models.
2. Express the likelihood functions for
the models.
3. Find the parameters that maximize
the likelihood functions.
4. Compare the values of likelihood to
decide which model is best.

15. 2.1.3 Find the parameters that
maximize the likelihood

16. Maximum Likelihood Estimate
A maximum likelihood (ML) estimate is the
parameter value that maximizes the likelihood
function for a given set of data.
- Definition 27（與前提）

17. 得到maximum likelihood estimators
(MLEs)的兩種基本方法
(1) 使用微積分
(2) 使用數值方法（ numerical method ） 來
找到能最大化likelihood的參數

18. 使用兩種方法前，最大化likelihood需：
取likelihood的自然對數（natural logarithm ）
做為主要使用的函數。
The first step in maximizing a likelihood is to use the
natural logarithm of the likelihood (the log likelihood,
denoted by l) as the main function of interest.

19. 取log前

20. 取log後

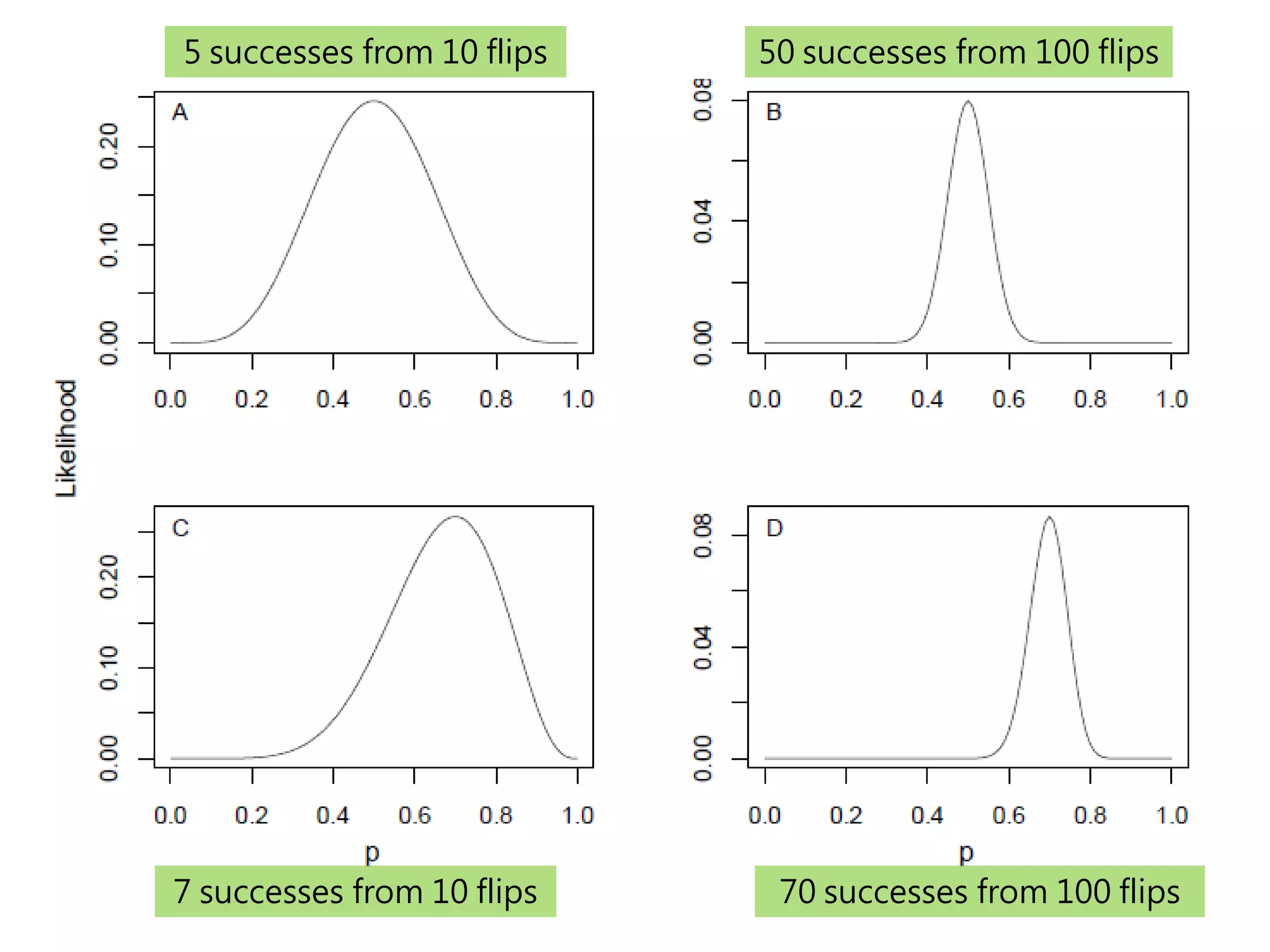
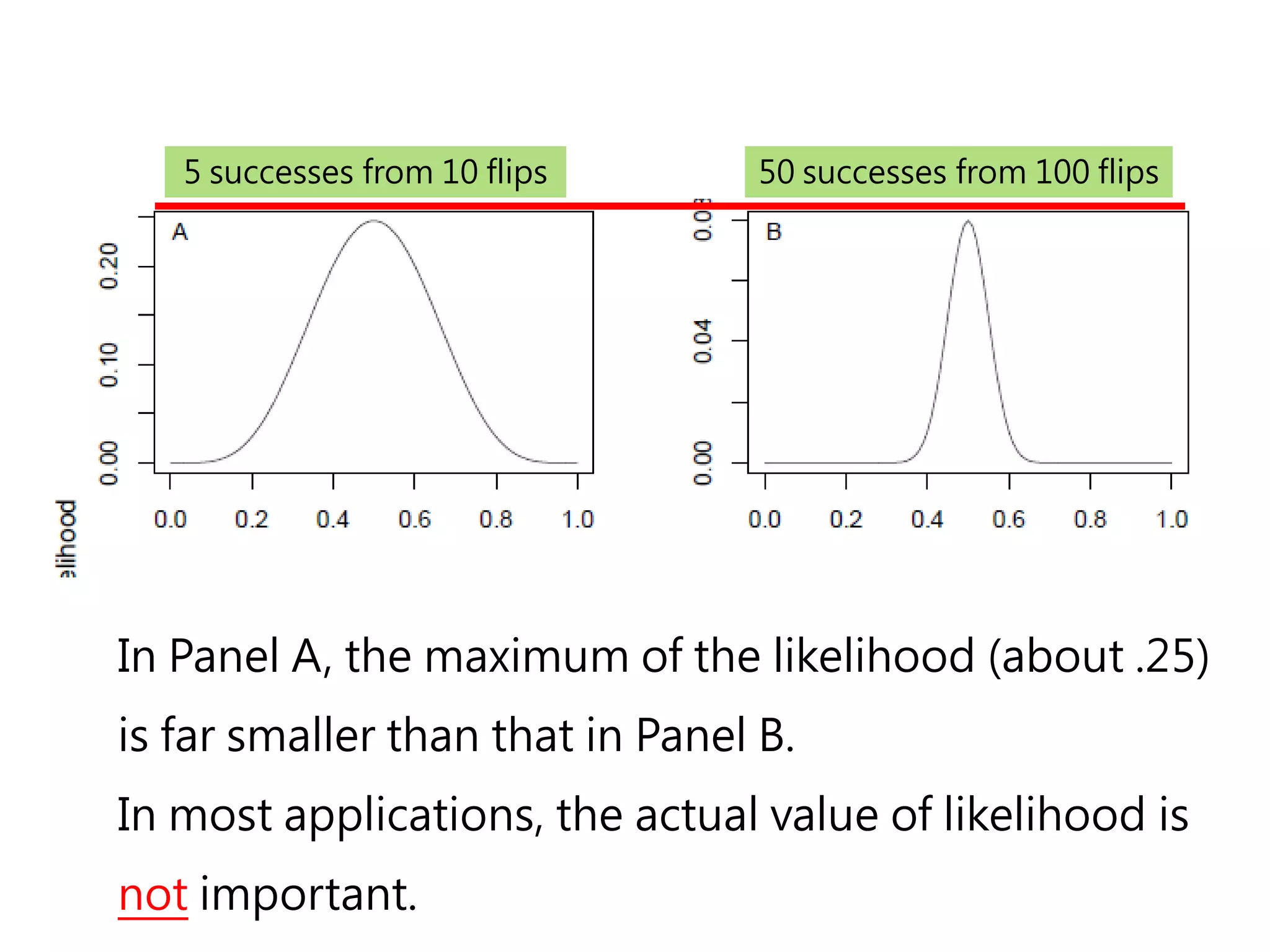
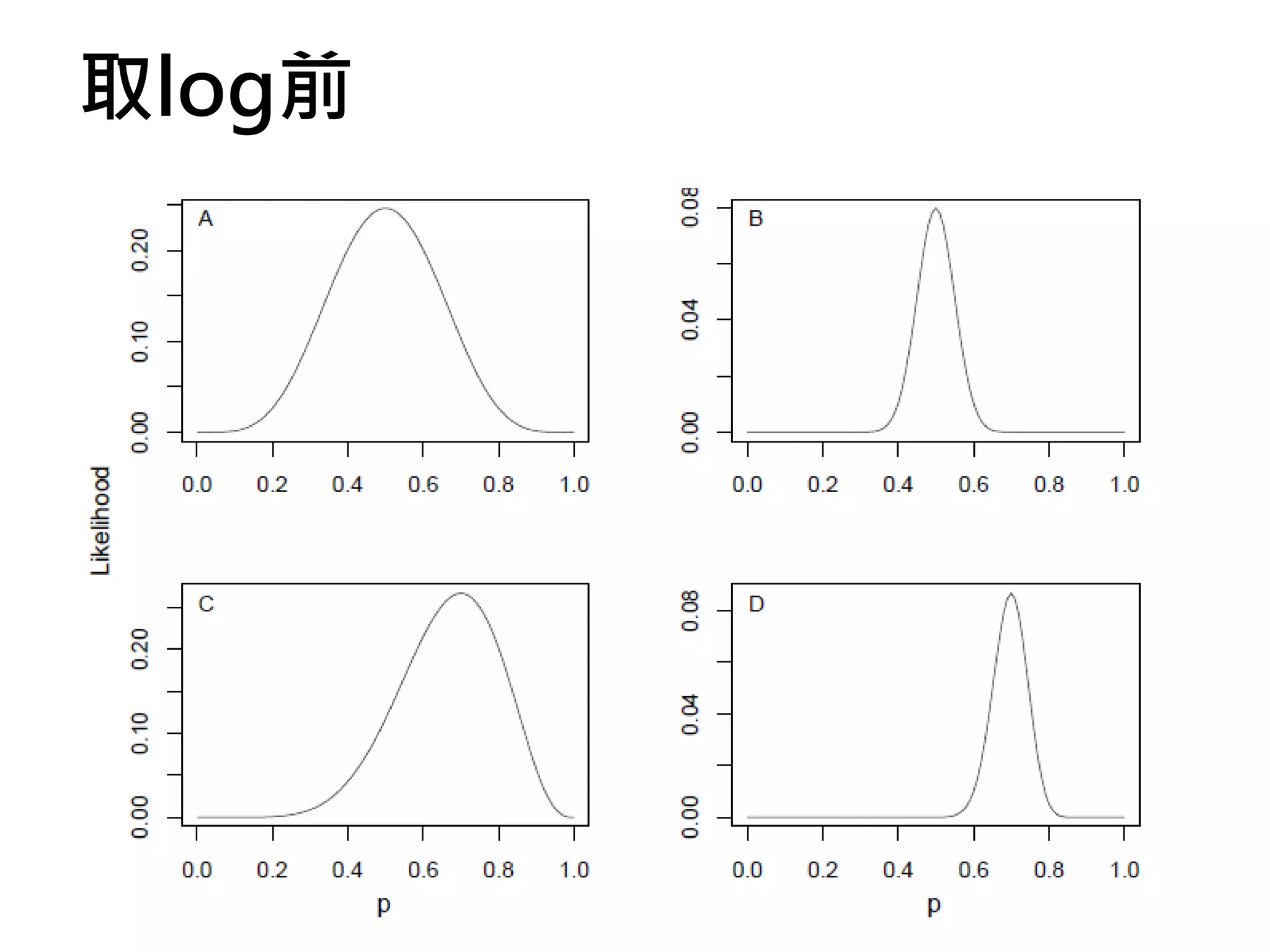
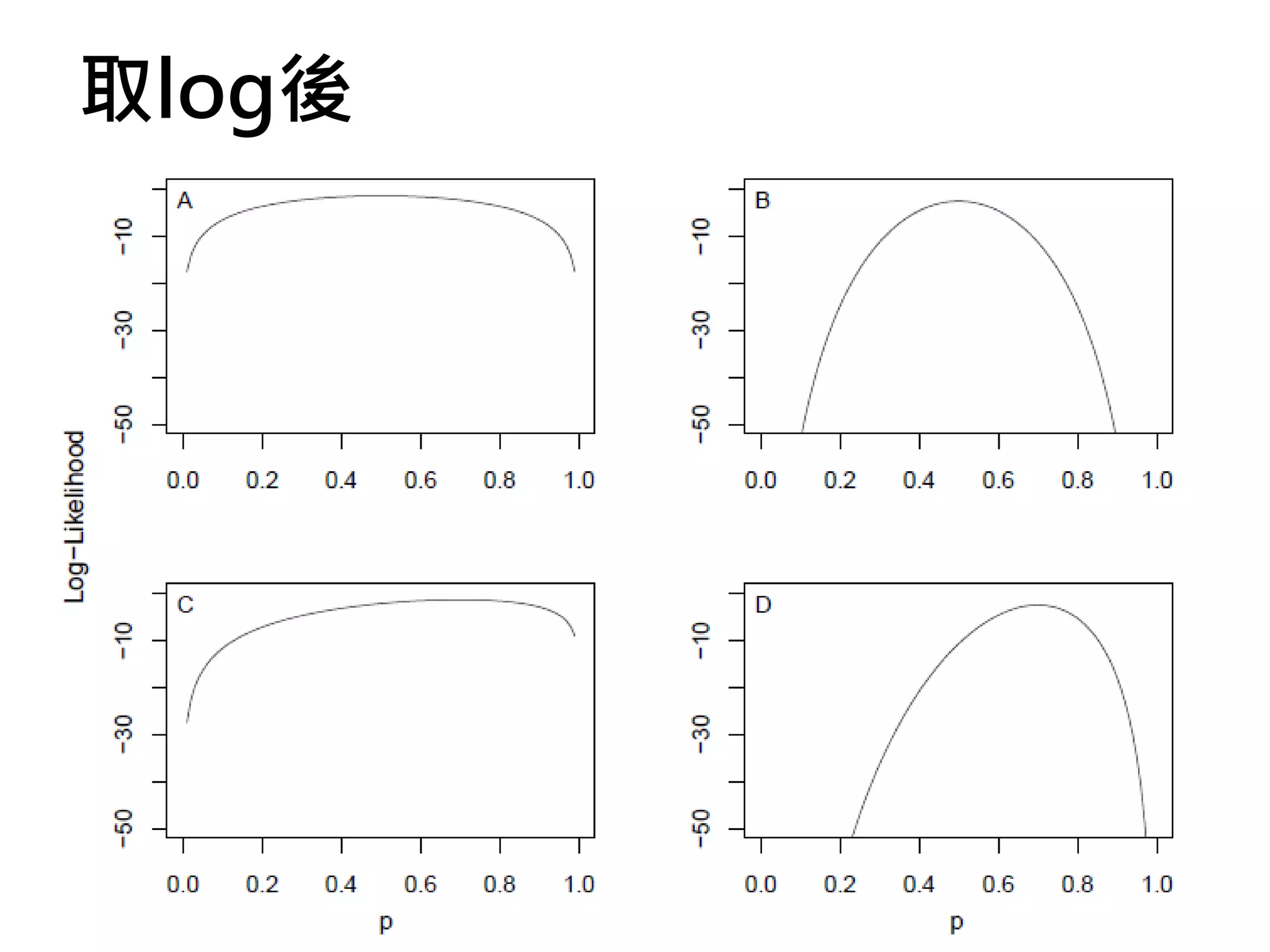
21. 如何取binomial的log
l ( p;y ) = log[L( p; y )] N y
L( p; y ) =   p (1 − p )
N−y
 y
 
 N  y N−y 
= log   p (1 − p ) 
 y
  
N
( ) (
= log  + log p + log (1 − p )
 y
y N−y
)
 
N
= log  + y log p + ( N − y ) log(1 − p )
 y
 

22. 使用Matlab對likelihood
function取log，並繪圖
p=0:.01:1
like1 = log(bilike(p,5,10))
like2 = log(bilike(p,50,100))
like3 = log(bilike(p,7,10))
like4 = log(bilike(p,70,100))
plot(p,like1,p,like2,p,like3,p,like4)

23. Log likelihood Function
The log likelihood function is the
natural logarithm of the likelihood
function.
N
log  + y log p + ( N − y ) log(1 − p )
 y
 
- Definition 28

24. Log likelihood Function
對兩種方法都很有用。

25. 有了log likelihood function，接下來要算
Maximum Likelihood Estimate

26. 2.1.4 Calculus Methods
to find MLEs
The calculus methods are limited in their
application and many problems must be
solved with numerical methods.

27. 我們的目標是找到能最大化log likelihood
function（i.e., l(p; y)）的p值
N
l(p; y) = log  + y log p + ( N − y ) log(1 − p )
 y
 
微分！

28. Step 1. 對p進行微分
∂l ( p; y ) ∂   N  
= log  + y log p + (N − y ) log(1 − p )
∂p ∂p   y 
  
∂   N  ∂ ∂
= log  + [ y log p ] + [( N − y ) log(1 − p )]
∂p   y  ∂p
  ∂p
y N−y
= 0+ −
p 1− p
y N−y
= -
p 1− p

29. Step 2.
y N−y
使上式等於0， - = 0,
p 1− p
求p的解 y N−y
= ,
p 1− p
(1 − p ) y = (N − y ) p,
y − py = Np − yp,
y = Np,
y
p=
ˆ
N

30. y
p=
observed successes
ˆ
N
For a binomial, the proportion of
successes is the maximum
likelihood estimator of parameter p.

31. Problem 2.1.2 (Your Turn)
Using calculus methods, derive the
maximum likelihood estimator of
parameter λ in the Poisson distribution
(see Eq. 2.3).