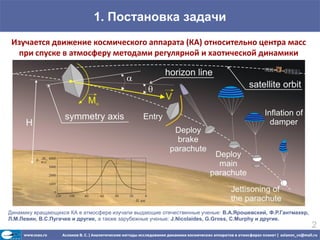
Документ представляет исследование динамики космических аппаратов в атмосфере планеты Венера, включая рассмотрение различных методов аналитической динамики. Основное внимание уделяется построению математических моделей движения космических аппаратов, анализу невозмущенных и возмущенных движений, а также определению устойчивости и резонанса в их динамике. В исследовании рассматриваются известные миссии на Венеру и их характеристики.

1. Асланов Владимир Степанович
aslanov_vs@mail.ru
Аналитические методы исследования
динамики космических аппаратов в
атмосферах планет
Кафедра теоретической механики
www.termech.ru
Самарский государственный аэрокосмический университет
им. академика С. П. Королѐва
www.ssau.ru
2012 год

2. 1. Постановка задачи
Изучается движение космического аппарата (КА) относительно центра масс
при спуске в атмосферу методами регулярной и хаотической динамики
Динамику вращающихся КА в атмосфере изучали выдающие отечественные ученые: В.А.Ярошевский, Ф.Р.Гантмахер,
Л.М.Левин, В.С.Пугачев и другие, а также зарубежные ученые: J.Nicolaides, G.Gross, C.Murphy и другие.
2

3. 1. Постановка задачи
Изучение планеты Венера (СССР: 1961-1983, СА «Венера 1 – 14», «Вега 1-2» )
СА «Венера 12»– 4700 кг
1967 г. «Венера 4» - посадка
на поверхность Венеры
1975 г. «Венера 9-10» -
время работы на
поверхности Венеры:
53 мин.
1983 г. «Вега 1-2» -
аэростатный зонд, H=55км,
время работы: 46 часов
Венера: атмосфера- 90% углекислого газа, температура – 500 oС, давление – 100 атм.
3

4. Примеры КА, предназначенных для входа в
атмосферу
4

5. 1. Постановка задачи
Цель работы
• Построение простых математических моделей пространственного
движения КА относительно центра масс в атмосфере. Разделение
движения на невозмущенное и возмущенное.
• Получение точных и приближѐнных аналитических решений,
описывающих движение КА в невозмущенном движении.
• Вывод приближѐнных аналитических решений, описывающих
возмущенные колебания КА, вызванных изменением параметров
атмосферы.
• Выявление нелинейного резонанса, определение устойчивости
резонанса для возмущенного движения.
• Описание движения КА в атмосфере методами хаотической
динамики.
• Восстановление (идентификация) движения КА по результатам
измерений.
5

6. 2. Уравнения движения
Уравнения движения КА в инерциальной системе отсчета
   
dK    dei  
2
d r  F
 K  M,    ei  0, 2
g (1)
dt dt dt m
 Системы координат

где K  I   - кинематический момент КА,

I - тензор инерции,  - угловая скорость,
  - аэродинамическая сила и момент,
F, M

ei - единичные векторы,
m - масса,

g - гравитационное ускорение.
6

7. 2. Уравнения движения
Уравнения движения центра масс КА
dV qS d cos   V2  dH
 cxa  g sin  ,   g  ,  V sin  (2)
dt m dt V  r  dt
  H V 2
где V , H ,  - скорость, высота и угол наклона траектории; q  - скоростной напор
2
Iz  I y
Малая асимметрия:   ( yT , zT , i  , I xy , I xz , mx , my , mz )  0( ) (3)
I
где  - малый параметр
Уравнения движения КА относительно центра масс
d 2
2
 F ( , z )   Ф ( ,  , z ),
dt
d
 R / I x  (G  R cos  ) cos  / sin 2   Ф ( , z ), (4)
dt
dz
  Фz ( ,  , z ), ( z  R, G, q )
dt
где F (, z )  (G  R cos )(R  G cos ) / sin3   M  (, z ), (5)
 Ф  D0 ( , z )  D1 ( , z )sin   D ( , z ) cos   D3 ( , z )sin 2  D ( , z) cos 2
 
2

4
(6)
   , R, G, q  7

8. 3. Невозмущенное движения
Уравнения невозмущенного движения КА относительно центра масс  0
d 2  G  R cos   R  G cos  
  M    0 (7)
dt 2 sin 3 
qSL
Восстанавливающий момент M     m   , m    a sin   b sin 2 (8)
I
xT
где xT 
L
 *  0,  *  0, *   - положения равновесия
8

9. 3. Невозмущенное движения
Типы КА
m    a sin   b sin 2
m    a sin 
9

10. 3. Невозмущенное движения
Интеграл энергии системы (7)
1  d  R 2  G 2  2 RG cos 
2
    a cos   b cos 2   E (9)
2  dt  2sin 2
Замена переменных u  cos  приводит к уравнению
2
 du 
   f u  (10)
 dt 

где f  u   2 1  u
2
 E  au  bu   2GRu  G
2 2
 R2 (11)
Уравнение (10) интегрируется в квадратурах
u u
du du
t  t0  
u0 f u 
 
u0 a0u  a1u  a2u  a3u  a4
4 3 2 (12)
Интеграл (12) приводится к неполным эллиптических интеграла 1-го, 2-го и 3-го рода:

d  
d
F ( , k )  

, E ( , k )  1  k sin  d , П ( , n, k )  
2 2
0 1  k 2 sin 2  0 0 (1  n sin 2  ) 1  k 2 sin 2 
10

11. 3. Невозмущенное движения
Общее решение для m    a sin 
cos   (u1  u2 )cn 2   (t  t0 )  K , k   u2 (13)
где cn   (t  t0 )  K , k   cos am   (t  t0 )  K , k  - эллиптический косинус

K  k   F ( , k ) - полный эллиптический интеграл 1-го рода
2
  am   (t  t0 )  K , k  - амплитуда-функция
Приближенное решение
cos   B(1  cos y)(m  cos y)2  u2 (14)
Здесь y   (t  t0 ) / K , B  (u1  u2 ) p / 8, m  (2  p) / p,
2
 
p  2 1 1 k 2 / 1 1 k 2 
Угол собственного вращения
 R  G  R cos   t   cos  
t
  0    
sin 2   t 

 dt  f П   t  , n1 , k  , П   t  , n2 , k  , П  n1 , k  , П  n2 , k  
0  
 Ix 
(15)
11

12. 3. Невозмущенное движения
Общее решение для m    a sin   b sin 2
M
cos   u  L  (16)
1  Ncn 
 t 0, k 
где   1, 2 зависит от вида корней полинома f  u   0
Угол собственного вращения [Серов В.М.]
 R  G  R cos   t   cos  
t
  0    
sin 2   t 

 dt  f ab П   t  , n1 , k  , П   t  , n2 , k  , П  n1 , k  , П  n2 , k  
0  
 Ix 
12

13. 4. Возмущенное движения
4.1. Простейший вид возмущенного движения
(асимметрия и демпфирование отсутствуют)
Уравнение движения
d 2  G  R cos   R  G cos   dq
  a  q  sin   b  q  sin 2  0,   Фq  t  (17)
dt 2 sin 3  dt
Зависимость скоростного напора от Зависимость угла атаки от
времени времени
13

14. 4. Возмущенное движения
Адиабатический инвариант- интеграл возмущенного движения
 max
d 1  d 
T 2
Ig 

 dt
d     dt  const
2 0  dt 
(18)
min
Подставляя решения (13) или (16) в (18), получим неявную зависимость
амплитуды угла атаки от скоростного напора
V 2
I g (q  ,  max )  f  K  k  , E (k ), i (k , ni )   const (19)
2
Приближенные решения вида
 max   max  q  (20)
Минимальный угол атаки определяется из интеграла энергии (9) при
 d 
E  0   E  max   E  min  (21)
 dt 
14

15. 4. Возмущенное движения
4.2. Возмущенного движения осесимметричного КА
(асимметрия отсутствуют)
Уравнение движения
d 2  G  R cos   R  G cos  
  a  q  sin   b  q  sin 2   Ф  , z  ,
dt 2 sin 3 
(22)
dz
  Фz ( , z ), ( z  R, G, q)
dt
Сравнение результатов
где Ф , z  , z   Ф , z   2 , z  
Усредненные уравнения (метод Волосова)
d max   1 t T 1
t T
E
F ( max , z )  T  T  z
    dt 
  z dt 
dt
 t t
 W ( max , z ) 
  z     z  , (23)
z 
t T
dz 

dt T t   z ( (t ), z)dt   z  z  ,

где  , z  z    , z K  k  , E (k ),  i (k , ni ) 
15

16. 4. Возмущенное движения
4.3. Возмущенного движения асимметричного КА
Уравнение движения в виде двухчастотной системы
y  ( z )  Y ( y, , z ),

  Ф ( y, z ),
 (24)
z  Фz ( y, , z ),

Фz  D0z ( y, z)  D1z ( y, z) sin  D2z ( y, z) cos  D3z ( y, z) sin 2  D4z ( y, z) cos 2.
где z  ( R, G ,  max , q ), y  (t  t0 ) - фаза колебания угла атаки
Фz  y,  , z   Фz  y  2 ,   2 , z  , Ф  y, z   Ф  y  2 , z  ,
(25)
Y  y,  , z   Y  y  2 ,   2 , z 
Средняя частота собственного вращения
2
1
2 
( z )  Ф ( y, z )dy (26)
0
16

17. 4. Возмущенное движения
Нелинейный резонанс
( z )  m( z )n( z )O() (27)
где m, n - целые, простые числа
Приближенные формулы для частот (b=0):
 1 1 R2
  2   R / 4,
2
a
2
  R     sign( R  G ) a 
2
(28)
 Ix 2  4
Главный резонанс (m=n):    (29)
Резонанс крена (m=0):   0 (30)
17

18. 4. Возмущенное движения
Пример резонансного вращения (b=0)
qSl  qSl
  F ( )  zт cos  sin 
 , R   zт sin  cos  , q   Фq ( z ), G  const (31)

I I
Главный резонанс (m=n): 
точка 2
Точка 1:
y  0,   0, N1  qS sin  max , M R   z  qSl sin  max N2
N1
N3
Точка 2:
точка 1 точка 3
 
y ,  , N 2  qS sin  , M R  0 N4
2 2
Точка 3:
y   ,    , N3  qS sin  min , M R  z  qSl sin  min
Точка 4: точка 4
3 3
y ,  , N 4  qS sin  , M R  0
2 2
18

19. 4. Возмущенное движения
Маятниковая система. Анализ резонансов
Замена переменных:  = my / n   (32) Фазовый портрет
Маятниковая система
d 2 dz
+Q( ,z)=0,   f z (  ,z) (33)
d 2
d
где    ,
Q(  , z )  Q0 ( z )  Q1 ( z )sin  
(34)
 Q2 ( z ) cos   Q3 ( z )sin 2   Q4 ( z ) cos 2 
Интеграл энергии    0
2
1  d 
   W ()  E (35)
2  d 
где W ( ,z)  Q0   Q1 cos   Q2 sin   (36)
1 1
 Q3 cos 2   Q4 sin 2  .
2 2 19

20. 4. Возмущенное движения
Захват и проход через резонанс
Главный резонанс и резонанс крена Типы движений
 рад.
 проход
захват
 min *  max

t,сек движение в малой
0 50 100 150 200 окрестности центра
20

21. 4. Возмущенное движения
Устойчивость резонанса
Замена переменных    *   ,    *   ,    d  / d ,  *  0  (37)
Уравнения возмущенного движения в окрестности центра   *
d  d 
    G (  * , z ),   2 (  * , z )   P(  * , z ),
d d
(38)
dz
  f z ( * , z)
d
Q Q Q
где G (  , z )    f z (  * , z ),  2 (  * , z )  0 (39)
*
/ 
  z      *   *
Функция Ляпунова
VA 2
   22
2

21

22. 4. Возмущенное движения
Влияние резонанса на движение КА
  гр ад
150
устойчивы й резонанс
125
неустойчивы й резонанс
100
75
50
проход
25
безрезонансное движ ение
h,км
0
65 45 25 5
 к  /с
11 безрезонансное движ ение
проход
10
9
8
7
6
неустойчивы й резонанс
5
4 устойчивы й резонанс h,км
65 45 25 5
22

23. 4. Возмущенное движения
4.4. Особенности возмущенное движение КА с бигармоническим моментом
Бигармонический момент Фазовый портрет
m  , t   a  t  sin   b  t  sin 2
Три положения равновесия:
 *  0,  *  0, *  
Три области существуют, если W   u*1   W   u*2   0 (40)
где u*1 , u*2 корни уравнения W   u   0 (41)
23

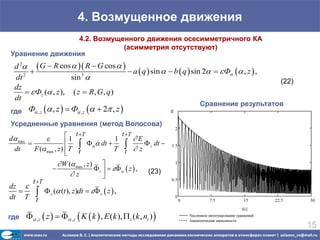
24. 4. Возмущенное движения
A0-stable; A1,A2 - unstable A0-unstable; A1,A2 - stable
A1,A2 – stable if   
E ( z )  W* or f*  0 (42)
A0 – stable if   
E ( z )  W* or f*  0 (43)
E - average value of the total energy, calculated in neighborhood separatrix
W* - value of the potential energy, calculated at the saddle point u=u*
   
f  f (u , z )  2(1  u 2 )[ E ( z )  W (u , z )]  O( 2 ) (44)
* * * *
24

25. 4. Возмущенное движения
E ( z )  W  m , z  (45)
   m - the amplitude value of the angle of attack
The derivatives by virtue of the averaged equations
 W W W
E ( z)  m 
  z  F ( m , z )   m 
  z
 (46)
   m z   m z   m
 W
W (* , z )  z
 (47)
z  *
The criterion of stability of the disturbed motion in neighborhood the separatrix
m
W (48)
  F ( m , z )   m 
 z

z *
A1,A2 – stable if 0 (49)
A0 – stable if 0 (50)
25

26. 4. Возмущенное движения
At the moment of time t* the phase trajectory
intersects the separatrix. Areas A1 and A2 are
stable, therefore the system can continue the
further motion both in area A1, and in area A2.

27. 5. Хаотические колебания КА
Хаотическое поведение асимметричного тела
с бигармоническим моментом (классическая постановка)
Новые обозначения: угол нутации    , моменты инерции A  I x , B  I y , C  I z ,

обобщенные импульсы p  I x , p  I x R, p  I xG.
Малый параметр    B  A / A (51)
Гамильтониан: H  H 0   H1  O( 2 ) (52)
p  p  p cos  
2
2 2
p
где H 0     a cos   b cos2  (53)
2A 2 A sin 2  2C
 p  p cos   cos   p sin  sin  
2
H1    
(54)
2 A sin 
2
Канонические уравнения
H H
qi 

pi
, pi  

qi

, qi   ,  , , pi  p , p , p  (55)
27

28. 5. Хаотические колебания КА
Невозмущенная система   0  H  H0
  p , p    
p  p cos   p  p cos  
   a sin   b sin 2 ,
A A sin 3 
(56)
p  p  p cos   cos   p  p cos  , p , p  co nst
   ,   
C A sin 2  A sin 2 
Случай Эйлера: a=0, b=0. Случай Лагранжа: a>0, b=0.
Гомоклинические (сепаратрисные)
траектории
4
cos  ( j ) (t )  u0  , j  1, 2
2   (4   )C j exp(t )  C j exp( t )
2 1
(57)
28

29. 5. Хаотические колебания КА
Функция Мельникова

 H 0 H 0 H 0  ( j )
M j  t0     g p  g  g p   (t  t0 ), p (t  t0 ), p ,   t  t0   dt 
( j) ( j)
 
 p  p  (58)

  0 , p   g p  ( j ) (t  t0 ), p ( j ) (t  t0 ), p ,  ( j )  t  t0  dt

Функция Мельникова для
областей А1 и А2
где
H1 H H1
g  , g p   1 , g 
p  p
29

30. 5. Хаотические колебания КА
Сечения Пуанкаре
Инерционная асимметрия Инерционная асимметрия
 0   0.01
30

31. 5. Хаотические колебания КА
Сечения Пуанкаре
Инерционная асимметрия
  0.05
Перетекание хаотических траекторий 31

32. 6. Хаотические колебания КА с подвижным
центром масс
Центр масс КА перемещается вдоль оси симметрии
xc  ( xc )0  xc sin(t ) (59)
Уравнение движения КА


 G  R cos   R  G cos    a sin   b sin 2 
sin  3
(60)
  ( a sin   b sin 2 ) sin(t )   m ( )
Система Мельникова
    f1  g1 ,

    G  R cos   R  G cos   / sin 3   a sin   b sin 2 

(61)
 (a sin   b sin 2 ) sin    1  sin     f 2  g 2 ,
2

 
32

33. 6. Хаотические колебания КА с подвижным
центром масс
Гомоклинические траектории
4
cos  ( j ) (t )  u0  , j  1, 2 (62)
2   (4   )C j exp(t )  C j exp( t )
2 1
Функция Мельникова

M (t0 , 0 )   { f1[qi ) (t )] g2[qi ) (t ), t  t0  0 ]}dt  M (i )  M (i )
(i )

( (
(63)


где M      i ) (a sin  i )  b sin 2 i ) ) sin(t  t0  0 )dt ,
(i ) ( ( (

 (64)
M     (1  sin  )( ) dt
(i ) 2 (i )

(i ) 2


Условие отсутствие хаоса
M(i )  M (i ) (65)
33

34. 6. Хаотические колебания КА с подвижным
центром масс
Сечения Пуанкаре
34

35. 7. Восстановление (идентификация) движения КА
по результатам измерений
7.1. Общие положения интегрального метода
(66)
Вектор измерений: d  (d1 , d 2 ,.., d m )
Вектор расчетных значений: g ( )   g1 , g 2, ..., g m  (67)
где 
  1,2, ..., l  - вектор определяемых параметров

 
N m
Метод наименьших квадратов (МНК)   argmin   j d ij  g ij  
2
(68)
 i 1 j 1
Пусть известна совокупность независимых интегралов
 
H k ,d j  const, k  1,2,.. p; j  1,2,..m (69)
или медленно меняющихся функций

dH k ,d j   O (70)
dt
Новый критерий оценки состояния
 k  H k  , dij   H k  , gij   
N p 2

  arg min (71)

i 1 k 1
 
35

36. 7. Восстановление (идентификация) движения КА
по результатам измерений
7.2. Идентификация вращательного движения КА
на орбитальном участке
Измеряется угловая скорость x 
d  u ,u ,u
y z  (72)
   x 0 ,  y 0 ,  z 0 , I x , I y , I z 
(73)
Вектор определяемых параметров
Существует три первых интегралов, зависящих от угловой скорости
 K x x   y K y   z K z  / 2  H1 ,
K x2  K y  K z2  H 2 ,
2 (74)
K x  K y   K z   H 3

где K  I     K x , K y , K z  - кинетический момент, , ,  - направляющие косинусы.

Новый критерий оценки состояния
 k  H k  ,  uji   H k  ,  jip    , j  x, y, z
N 2 2

  arg min (75)
 
i 1 k 1

36

37. 7. Восстановление (идентификация) движения КА
по результатам измерений
Пример
Число измерений угловой скорости N=20
Математические ожидания и среднеквадратические отклонения оценок
моментов инерции для различных интервалов измерения t 
Метод наименьших квадратов Интегральный метод
t 2 10 25 40 2 10 25 40
MIx 1.499 1.499 1.499 1.493 1.491 1.494 1.499 1.500
I x 0.011 0.009 0.437 0.571 0.082 0.063 0.092 0.074
MIy 5.627 5.619 6.477 7.007 5.604 5.604 5.612 5.605
I y 0.027 0.025 1.651 3.183 0.043 0.046 0.041 0.043
Преимущества интегрального метода:
1. Точность метода мало зависит шага измерения .
2. Для получения оценок не требуется большой объем вычислений.
37

38. 7. Восстановление (идентификация) движения КА
по результатам измерений
7.3. Идентификация вращательного движения КА при спуске в
атмосфере

Измеряется угловая скорость и перегрузки d  x ,  y , z , nx , n y , nz  (76)
Вектор определяемых параметров    x0 , D  (77)
где x0 - вектор начальных условий,
D - вектор параметров КА.
Существует три медленно меняющиеся функции
R  I x x , G
1
n
 I x x nx   y n y   z nz  ,
(78)
1  n 1
c n  
i 1
E  I x x  I  y  I  z2  q  i  x  
2 2
2I 
 i 0 i  1  n  

где E - кинетическая энергия.
Новый критерий оценки состояния
     
N
  argmin   R Riu  Rip   E Eiu  Eip 
~ 2 2 2
 G Giu  Gip (79)
 i 1 
 

38

39. 7. Восстановление (идентификация) движения КА
по результатам измерений
Пример
Число измерений угловой скорости N=50
Математические ожидания и среднеквадратические отклонения оценок

запаса статической устойчивости m z для различных интервалов
измерения t 
t ,c 0.2 2.0 4.0 8.0 16.0
t ,c 0.011 0.105 0.221 0.421 0.842
M m
 -0.0599 -0.0599 -0.0799 - -
z
 m
 0.0006 0.0001 0.0306 - -
z
M ~ -0.0624 -0.0604 -0.0604 -0.0604 -0.0604
mz
 ~ 0.0033 0.0011 0.0011 0.0010 0.0012
mz
K m m
 ~ 0.5264 0.6579 0.0696 - -
z z
Преимущества интегрального метода:
1. Точность метода мало зависит шага измерения .
2. Для получения оценок не требуется большой объем вычислений.
39

40. Основные результаты опубликованы в
следующих статьях
• Асланов В.С. Пространственное движение тела в атмосфере, М:. Физматлит, 160 с., 2004.
• Aslanov V.S. Spatial chaotic vibrations when there is a periodic change in the position of the centre
of mass of a body in the atmosphere- Journal of Applied Mathematics and Mechanics 73 (2009) 179–
187.
• Aslanov V.S. and Ledkov A.S. Analysis of the resonance and ways of its elimination at the descent
of spacecrafts in the rarefied atmosphere - Aerospace Science and Technology 13 (2009) 224–231.
• Aslanov V.S. Resonance at motion of a body in the Mars’s atmosphere under biharmonical moment -
WSEAS TRANSACTIONS on SYSTEMS AND CONTROL, Issue 1, Volume 3, January 2008, (ISSN:
1991-8763), pp. 33-39.
• Aslanov V. S. and Doroshin A. V. Influence of Disturbances on the Angular Motion of a Spacecraft in
the Powered Section of Its Descent - Cosmic Research ISSN 0010-9525, Vol. 46, No. 2, 2008, pp. 166-
171.
• Aslanov V.S. Resonance at Descent in the Mars’s Atmosphere of Analogue of the Beagle 2 Lander -
Proceedings of 3rd WSEAS International Conference on DYNAMICAL SYSTEMS and CONTROL
(CONTROL'07), Arcachon, France, October 13-15, 2007, 178-181.
• Aslanov V. S. and Ledkov A.S. Features of Rotational Motion of a Spacecraft Descending in the
Martian Atmosphere - Cosmic Research ISSN 0010-9525, 2007, Vol. 45, No. 4, 331-337.
• Aslanov V. S. Doroshin A. V. and Kruglov G.E. The mothion of coaxial bodies of varying
composition on the active leg of descent - Cosmic Research ISSN 0010-9525, Vol. 43, No. 3, 2005, pp.
213-221.
40

41. Основные результаты опубликованы в
следующих статьях
• Aslanov V. S. The motion of a rotating body in a resisting medium - Mechanics of Solids, 2005, vol.
40, no2, pp. 21-32.
• Aslanov V.S. and Timbyi I.A. Action-angle canonical variables for the motion of a rigid body under
the action of a biharmonic torque - Mechanics of Solids, Vol. 38, No. 1, pp. 13-23, 2003.
• Aslanov V. S. and Doroshin A. V. Stabilization of a Reentry Vehicle by a Partial Spin-up during
Uncontrolled Descent - Cosmic Research ISSN 0010-9525, Vol. 40, No. 2, 2002, pp. 178-185.
• Aslanov V. S. and Myasnikov S. V. Analysis of Nonlinear Resonances during Spacecraft Descent in
the Atmosphere - Cosmic Research ISSN 0010-9525, Vol. 35, No. 6, 1997, pp. 616-622.
• Aslanov V. S. and Timbay I. A. Transient Modes of Spacecraft Angular Motion on the Upper Section
of the Reentry Trajectory - Cosmic Research ISSN 0010-9525, Vol. 35, No. 3, 1997, pp. 260-267.
• Aslanov V. S. and Myasnikov S. V. Stability of Nonlinear Resonance Modes of Spacecraft Motion in
the Atmosphere - Cosmic Research ISSN 0010-9525, Vol. 34, No. 6, 1996, pp. 579-584.
• Aslanov V. S. and Timbay I. A. Some Problem of the Reentry Vehicles Dynamics- Cosmic Research
ISSN 0010-9525, Vol. 33, No. 6, 1995.
• Aslanov V.S. Nonlinear Resonances of the Slightly Asymmetric Reentry Vehicles - Cosmic
Research ISSN 0010-9525, Vol. 30, No. 5, 1992.
• Aslanov V.S. Definition of Rotary Movement of a Space Vehicle by Results of Measurements -
Cosmic Research ISSN 0010-9525, Vol. 27, No. 3, 1989.
• Aslanov V.S. Two Kinds of Nonlinear Resonant Movement of an Asymmetric Reentry Vehicle -
Cosmic Research ISSN 0010-9525, Vol. 26, No. 2, 1988.
• Aslanov V. S. and Boyko V.V. Nonlinear Resonant Movement of an Asymmetric Reentry Vehicle -
Cosmic Research ISSN 0010-9525, Vol. 23, No. 3, 1985.
41

42. Основные результаты опубликованы в
следующих статьях
• Aslanov V. S., Boyko V.V. and Timbay I. A. Spatial Fluctuations of the Symmetric Reentry Vehicle at
Any Corners of Attack - Cosmic Research ISSN 0010-9525, Vol. 19, No. 5, 1981.
• Aslanov V. S. Definition of Amplitude of Spatial Fluctuations of the Slightly Asymmetric Reentry
Vehicles - Cosmic Research ISSN 0010-9525, Vol. 18, No. 2, 1980.
• Aslanov V. S. About Rotary Movement of the Symmetric Reentry Vehicle - Cosmic Research ISSN
0010-9525, Vol. 14, No. 4, 1976.
42