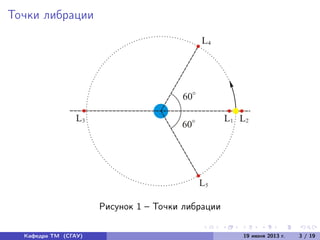
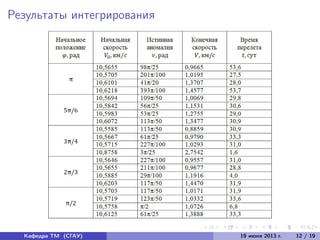
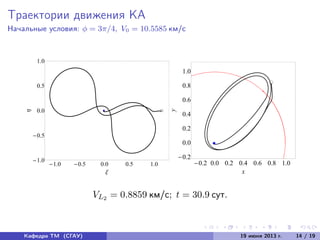
Документ представляет собой исследование различных вариантов перелета космического аппарата в точку либрации L2 системы Земля-Луна, выполняемое на кафедре теоретической механики. Основной целью является моделирование движения аппарата при различных начальных условиях и выбор оптимального варианта с минимальной скоростью попадания в точку L2. Документ содержит уравнения движения, практическое применение точек либрации и результаты численного интегрирования траекторий движения космического аппарата.

1. Исследование различных вариантов перелета космического
аппарата в точку либрации L2 системы Земля-Луна
Кафедра теоретической механики
Выполнил: Кисел¨ев А.К.
e-mail: Kiselev.alexandr.2012@yandex.ru
Научный руководитель: к.т.н., профессор Авраменко А.А.
e-mail: avramenko_a_a@mail.ru
Самарский государственный аэрокосмический университет
им. академика С. П. Корол¨ева
(национальный исследовательский университет)
19 июня 2013 г.

2. Цель и задачи работы
Цель
Моделирование движения космического аппарата при различных
начальных условиях старта с околоземной орбиты и выбор варианта с
минимальной скоростью попадания в точку L2.
Задачи
1 Составить уравнения движения космического аппарата для
ограниченной задачи трех тел;
2 Рассмотреть различные начальные условия старта с околоземной
орбиты и выбрать вариант с минимальной скоростью попадания в
точку L2.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 2 / 19

3. Точки либрации
Рисунок 1 – Точки либрации
Кафедра ТМ (СГАУ) 19 июня 2013 г. 3 / 19

4. Практическое применение точек либрации
В настоящее время несколько космических аппаратов размещены в
различных точках либрации Солнечной системы:
SOHO (англ. Solar and Heliospheric Observatory, ”Солнечная и
гелиосферная обсерватория”) находится на орбите в точке L1
между Землей и Солнцем.
WMAP (англ. Wilkinson Microwave Anisotropy Probe), изучает
реликтовое излучение – в точке L2 за орбитой Земли.
Advanced Composition Explorer – в точке L1 системы
Земля-Солнце.
Телескоп ”Гершель” и телескоп ”Планк”, запущенные 14 мая 2009
года, находятся в точке L2 системы Земля-Солнце.
Космический аппарат WIND, предназначенный для исследования
солнечного ветра. Аппарат запущен в 1994 году и функционирует
в настоящее время, находится в точке L1.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 4 / 19

5. Постановка задачи
Рисунок 2 – Система координат
Кафедра ТМ (СГАУ) 19 июня 2013 г. 5 / 19

6. Постановка задачи
Пусть m1, m2, m3 – массы Земли, Луны и космического аппарата
(КА) соответственно.
Допущения
1 Орбита Луны является круговой, т.е.
e = 1 −
b2
a2
= 0,
где e – эксцентриситет орбиты Луны; a и b – большая и малая
полуоси эллиптической орбиты.
2 Движение космического аппарата происходит в плоскости орбиты
Луны.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 6 / 19

7. Кинетическая энергия и силовая функция
Кинетическая энергия и силовая функция КА имеют вид:
T =
1
2
m3 ( ˙x − ˙νy)2
+ ( ˙y + ˙νx)2
+ ˙z2
, (1)
U = fm3
m1
r1
+
m2
r2
. (2)
где ν – истинная аномалия, f – гравитационная постоянная.
Закон движения Луны относительно Земли определяется из задачи
двух тел:
r =
p
1 + e cos ν
, c2
= f(m1 + m2)p,
dν
dt
=
c
r2
. (3)
где p и e – фокальный параметр и эксцентриситет кеплеровской
орбиты, c – константа интеграла площадей.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 7 / 19

8. Уравнения движения ограниченной задачи трех тел
При помощи функции Лагранжа L = T + U выписываем
дифференциальные уравнения движения КА:
¨x − 2 ˙ν ˙y − ¨νy − ˙ν2
x =
∂W
∂x
,
¨y + 2 ˙ν ˙x + ¨νx − ˙ν2
y =
∂W
∂y
, (4)
¨z =
∂W
∂z
.
Здесь через W обозначена силовая функция U разделенная на m3.
Сделаем в уравнениях (4) следующую замену переменных:
x = rξ, y = rη, z = rζ. (5)
Кафедра ТМ (СГАУ) 19 июня 2013 г. 8 / 19

9. Уравнения движения ограниченной задачи трех тел
Переходя к новой независимой переменной истинной аномалии ν
получим:
ξ − 2η =
1
1 + e cos ν
∂Ω
∂ξ
,
η + 2ξ =
1
1 + e cos ν
∂Ω
∂η
, (6)
ζ =
1
1 + e cos ν
∂Ω
∂ζ
.
где
Ω =
1
2
ξ2
+ η2
−
1
2
e cos νζ2
+ W, (7)
W =
1 − µ
r1
+
µ
r2
, µ =
m2
m1 + m2
. (8)
Кафедра ТМ (СГАУ) 19 июня 2013 г. 9 / 19

10. Начальные условия
Координаты
Для нахождения решения плоской круговой ограниченной задачи
трех тел численно проинтегрируем систему (6).
Начальные координаты:
x0 = x1 + (R1 + h) cos(φ), y0 = −(R1 + h) sin(φ), (10)
где x1 – абсцисса центра Земли,
h = 300 км – высота круговой орбиты КА,
φ – угол между направлениями из центра Земли на начальную
точку полета и начальное положение Луны.
Для перехода к безразмерным координатам воспользуемся
формулами (5):
x = rξ, y = rη.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 10 / 19

11. Начальные условия
Скорости
Начальная скорость:
V0 = Vh + ∆V0 − Ve, (11)
где Vh – скорость движения по круговой орбите; ∆V0 – приращение
скорости, необходимое для схода с круговой орбиты; Ve – скорость
вращения подвижной СК.
Vh =
fm1
R1 + h
, Ve = ω(R1 + h), (12)
где ω – скорость вращения подвижной СК, рад/с:
ω = 2.69 · 10−6 рад
с
.
Для h = 300 км: Vh − Ve = 7.7121 км/с.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 11 / 19

12. Результаты интегрирования
Кафедра ТМ (СГАУ) 19 июня 2013 г. 12 / 19

13. Траектории движения КА
Начальные условия: φ = π/2, V0 = 10.5758 км/с
0.0 0.2 0.4 0.6 0.8 1.0 1.2
0.4
0.2
0.0
0.2
0.4
0.6
0.8
1.0
Ξ
Η
0.2 0.0 0.2 0.4 0.6 0.8 1.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
x
y
VL2 = 1.0726 км/с; t = 6.8 сут.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 13 / 19

14. Траектории движения КА
Начальные условия: φ = 3π/4, V0 = 10.5585 км/с
1.0 0.5 0.0 0.5 1.0
1.0
0.5
0.0
0.5
1.0
Ξ
Η
0.2 0.0 0.2 0.4 0.6 0.8 1.0
0.2
0.0
0.2
0.4
0.6
0.8
1.0
xy
VL2 = 0.8859 км/с; t = 30.9 сут.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 14 / 19

15. Траектории движения КА
Начальные условия: φ = π, V0 = 10.6101 км/с
2 1 0 1
1
0
1
2
Ξ
Η
0.0 0.5 1.0 1.5 2.0
1.0
0.5
0.0
0.5
1.0
x
y
VL2 = 1.3707 км/с; t = 28 сут.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 15 / 19

16. Траектории движения КА
Начальные условия: φ = 3π/4, V0 = 10.8758 км/с
0.0 0.2 0.4 0.6 0.8 1.0 1.2
0.4
0.2
0.0
0.2
0.4
Ξ
Η
0.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2
0.2
0.0
0.2
0.4
0.6
xy
VL2 = 2.7542 км/с; t = 1.6 сут.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 16 / 19

17. Траектории движения КА
Начальные условия: φ = π, V0 = 10.5962 км/с
1.0 0.5 0.0 0.5 1.0
1.0
0.5
0.0
0.5
Ξ
Η
0.0 0.2 0.4 0.6 0.8 1.0
0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
x
y
V1 = 1.5765 км/с,
∆V = −0.625 км/с, VL2 = 0.0465 км/с, t = 3.87 сут.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 17 / 19

18. Список использованных источников
1. Маркеев, А.П. Точки либрации в небесной механике и
космодинамике [Текст]/А.П. Маркеев. – М.:Наука, 1978. – 312 стр.
2. Левантовский, В.И. Механика космического полета в элементарном
изложении [Текст]/В.И. Левантовский. – М.: Наука, 1980. – 512 стр.
3. Дубошин, Г.Н. Небесная механика. Аналитические и качественные
методы [Текст]/Г.Н. Дубошин. – М.: Наука, 1978. – 456 стр.
Кафедра ТМ (СГАУ) 19 июня 2013 г. 18 / 19

19. Благодарю за внимание!
Кафедра ТМ (СГАУ) 19 июня 2013 г. 19 / 19