Документ описывает различные методы решения нелинейных уравнений и систем, включая графические методы, метод половинного деления, метод Ньютона, метод секущих и методы простых итераций. Указываются условия применения этих методов, их достоинства и недостатки, а также алгоритмы для поиска корней. В работе также рассматривается решение систем нелинейных уравнений с применением метода Зейделя и метода Ньютона.

1. Методы вычислений
Методы решения нелинейных уравнений и систем
Кафедра теоретической механики
yudintsev@termech.ru
Самарский государственный аэрокосмический университет
им. академика С. П. Королёва
(национальный исследовательский университет)
1 мая 2012 г.

2. Нелинейные уравнения f(x)=0
Решение уравнений f(x) = 0
f(x) = 0 (1)
f(x) - любая нелинейная функция
Этапы решения задачи (1)
Отделение корней - определение интервалов [ai, bi], внутри
каждого из которых есть только один корень f(ξi) = 0.
Уточнение корней - поиск приближённого значения ξ∗
i внутри
интервала [ai, bi] с заданной точностью.
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 2 / 33

3. Нелинейные уравнения f(x)=0 Отделение корней
Отделение корней
Графический метод
Построение графика функции и приближенное определение её
нулей.
Определение интервалов [ai, bi], для которых выполняются условие
f(ai)f(bi) < 0, (2)
и сохраняется знак производной f (x).
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 3 / 33

4. Нелинейные уравнения f(x)=0 Отделение корней
Отделение корней
Метод половинного деления
Интервал [a, b] делится на 2, 4, 8, 16, ... подинтервалов.
На границах каждого подинтервала определяют знаки функции
f(x)
если знаки f(x) разные, то существует не менее одного корня
если дополнительно сохраняется знак производной f (x), то
существует точно один корень.
a ba1 a2 a3
f(x)
x
x1
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 4 / 33

5. Нелинейные уравнения f(x)=0 Уточнение корня
Методы уточнения корня
Метод половинного деления
Метод Ньютона (метод касательных)
Метод секущих (метод хорд)
Метод простых итераций
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 5 / 33

6. Нелинейные уравнения f(x)=0 Уточнение корня
Метод половинного деления
Условия применения метода
f(a)f(b) < 0;
f(x) непрерывна на отрезке [a, b].
Достоинства
Простой алгоритм
Нет дополнительных ограничений на функцию f(x), кроме
требования непрерывности
Недостатки
Медленная сходимость
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 6 / 33

7. Нелинейные уравнения f(x)=0 Уточнение корня
Метод половинного деления
Алгоритм
[a, b] → x1 = (b + a)/2 → [a, x1] → x2 = (a + x1)/2 → [x2, x1] → . . .
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 7 / 33

8. Нелинейные уравнения f(x)=0 Уточнение корня
Метод половинного деления
Алгоритм
1 на шаге k − 1 найден отрезок [ak−1, bk−1] ∈ [a0, b0] для которого
f(ak−1)f(bk−1) < 0;
2 найдем xk = (ak−1 + bk−1)/2
3 если f(xk) = 0, то xk – корень уравнения;
4 если f(xk) = 0, то из двух отрезков [ak−1; xk] и [xk; bk−1]
выбирается тот, на границах которого функция имеет разные
знаки, т.е.:
выбирается отрезок [ak−1; xk], если f(ak−1)f(xk) < 0:
ak = ak−1, bk = xk;
выбирается отрезок [xk; bk−1], если f(xk)f(bk−1) < 0:
ak = xk, bk = bk−1;
5 итерации повторяются пока ε ≥ bk − ak, т.е. пока не будет
достигнута заданная точность.
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 8 / 33

9. Нелинейные уравнения f(x)=0 Уточнение корня
Метод Ньютона
Требования к функции
1 Существование производных первого f (x) и второго f (x)
порядков;
2 f (x) = 0
3 Знакопостоянство производных f (x) и f (x) на отрезке [a, b]:
sgnf (x) = const
sgnf (x) = const
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 9 / 33

10. Нелинейные уравнения f(x)=0 Уточнение корня
Метод Ньютона
Алгоритм
1 Известно k-ое приближение корня – xk.
2 Вычисляется следующее приближение по формуле
xk+1 = xk + hk. (3)
Приращение hk определяется на основе разложения функции f(x)
в ряд Тейлора до слагаемого O(h2
k) в окрестности xk:
f(xk+1) = f(xk) + f (xk)hk
=0
+f (α)
h2
k
2
, α ∈ (xk, xk+1)
3 Приравнивая линейную часть разложения нулю, найдем hk
hk = −
f(xk)
f (xk)
(4)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 10 / 33

11. Нелинейные уравнения f(x)=0 Уточнение корня
Метод Ньютона
Алгоритм
xk+1 = xk −
f(xk)
f (xk)
, x0 =
a, f(a) · f (a) > 0
b, f(b) · f (b) > 0
(5)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 11 / 33

12. Нелинейные уравнения f(x)=0 Уточнение корня
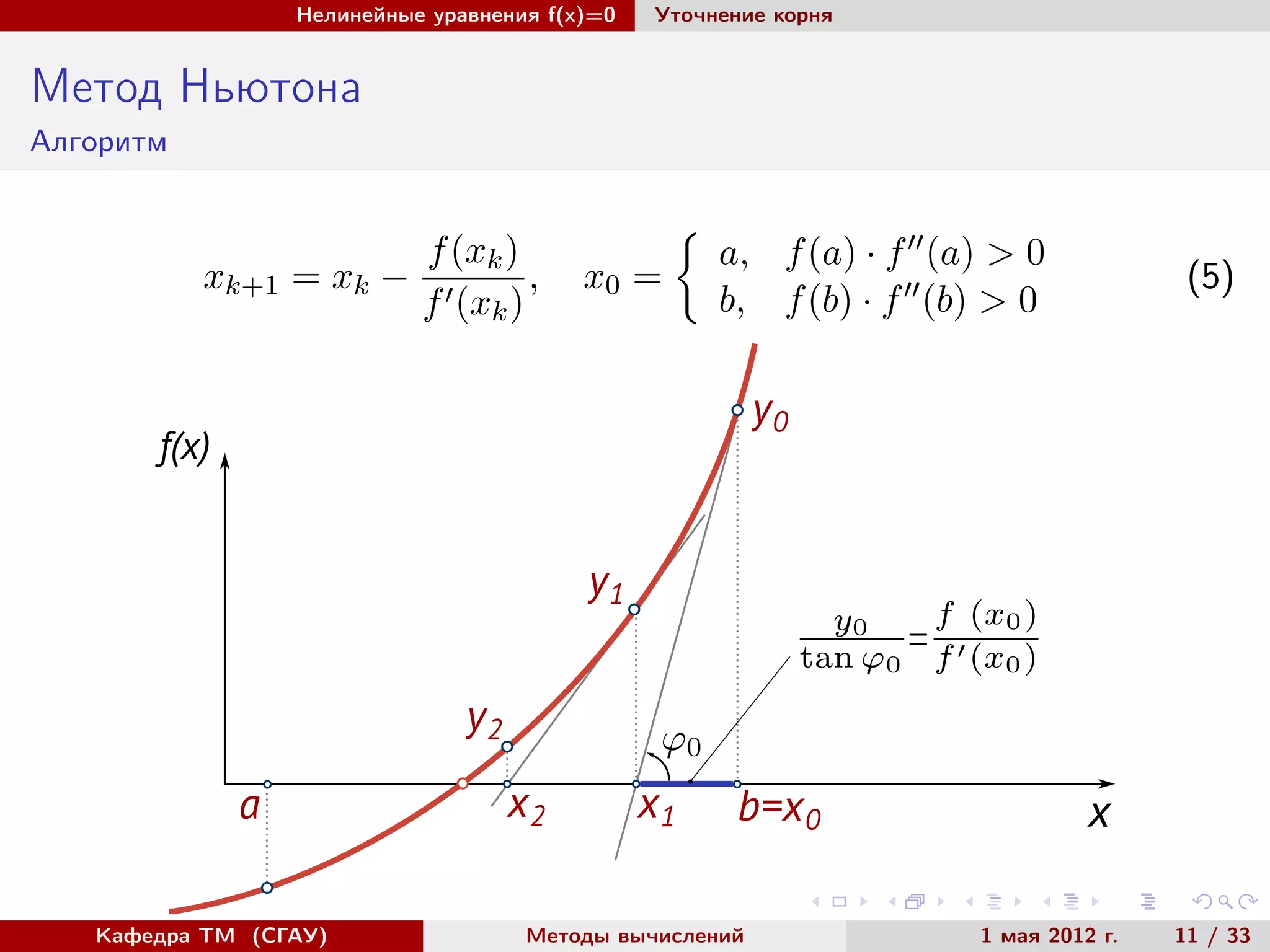
Метод Ньютона
Оценка погрешности
Для итерационного процесса метода Ньютона
xk+1 = xk −
f(xk)
f (xk)
(6)
погрешность оценивается неравенством
|ξ − xk+1| ≤
h2
k
2
M2
m1
(7)
где
M2 = max
x∈[a,b]
|f (x)|, m1 = min
x∈[a,b]
|f (x)|
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 12 / 33

13. Нелинейные уравнения f(x)=0 Уточнение корня
Модифицированный метод Ньютона
Значение производной вычисляется только один раз для начального
приближения.
xk+1 = xk −
f(xk)
f (x0)
, x0 =
a, f(a) · f (a) > 0
b, f(b) · f (b) > 0
(8)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 13 / 33

14. Нелинейные уравнения f(x)=0 Уточнение корня
Метод секущих
В методе Ньютона значение производной f (xk) заменяется на её
приближенное значение
f (xk) ≈
f(b) − f(xk)
b − xk
(9)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 14 / 33

15. Нелинейные уравнения f(x)=0 Уточнение корня
Метод секущих
Алгоритм с неподвижной правой границей
Если f(b) · f (b) > 0 : xk+1 = xk −
f(xk)
f(b) − f(xk)
(b − xk), x0 = a
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 15 / 33

16. Нелинейные уравнения f(x)=0 Уточнение корня
Метод секущих
Алгоритм с неподвижной левой границей
Если f(a) · f (a) > 0 : xk+1 = xk −
f(xk)
f(a) − f(xk)
(a − xk), x0 = b
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 16 / 33

17. Нелинейные уравнения f(x)=0 Уточнение корня
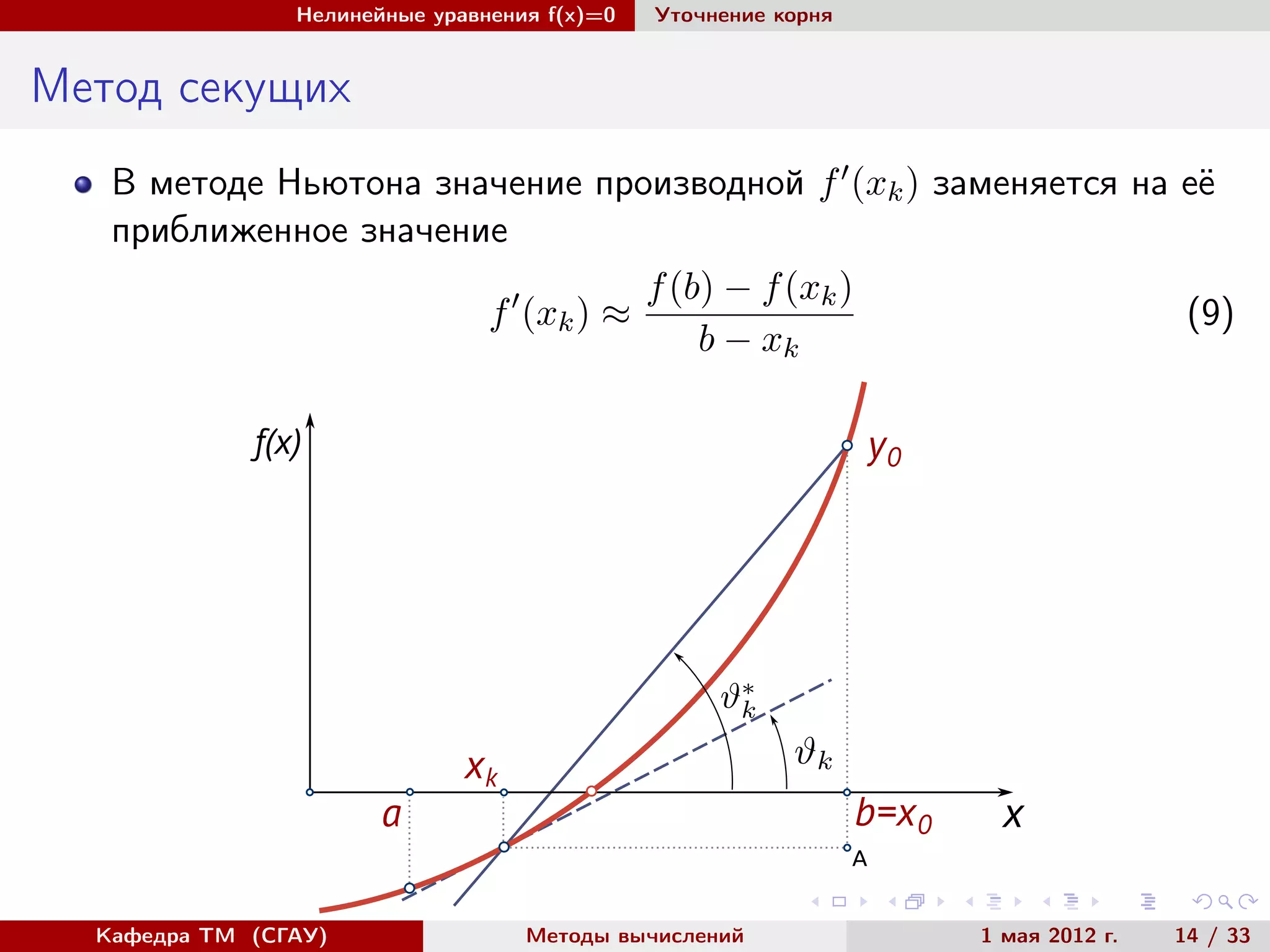
Метод простых итераций
Исходное уравнение заменяется на эквивалентное
f(x) = 0 → x = ϕ(x) , x ∈ [a, b] (10)
Строится итерационная последовательность
xk+1 = ϕ(xk), k = 0, 1, 2, . . .
Пример эквивалентного уравнения
x = x + f(x)
ϕ(x)
(11)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 17 / 33

18. Нелинейные уравнения f(x)=0 Уточнение корня
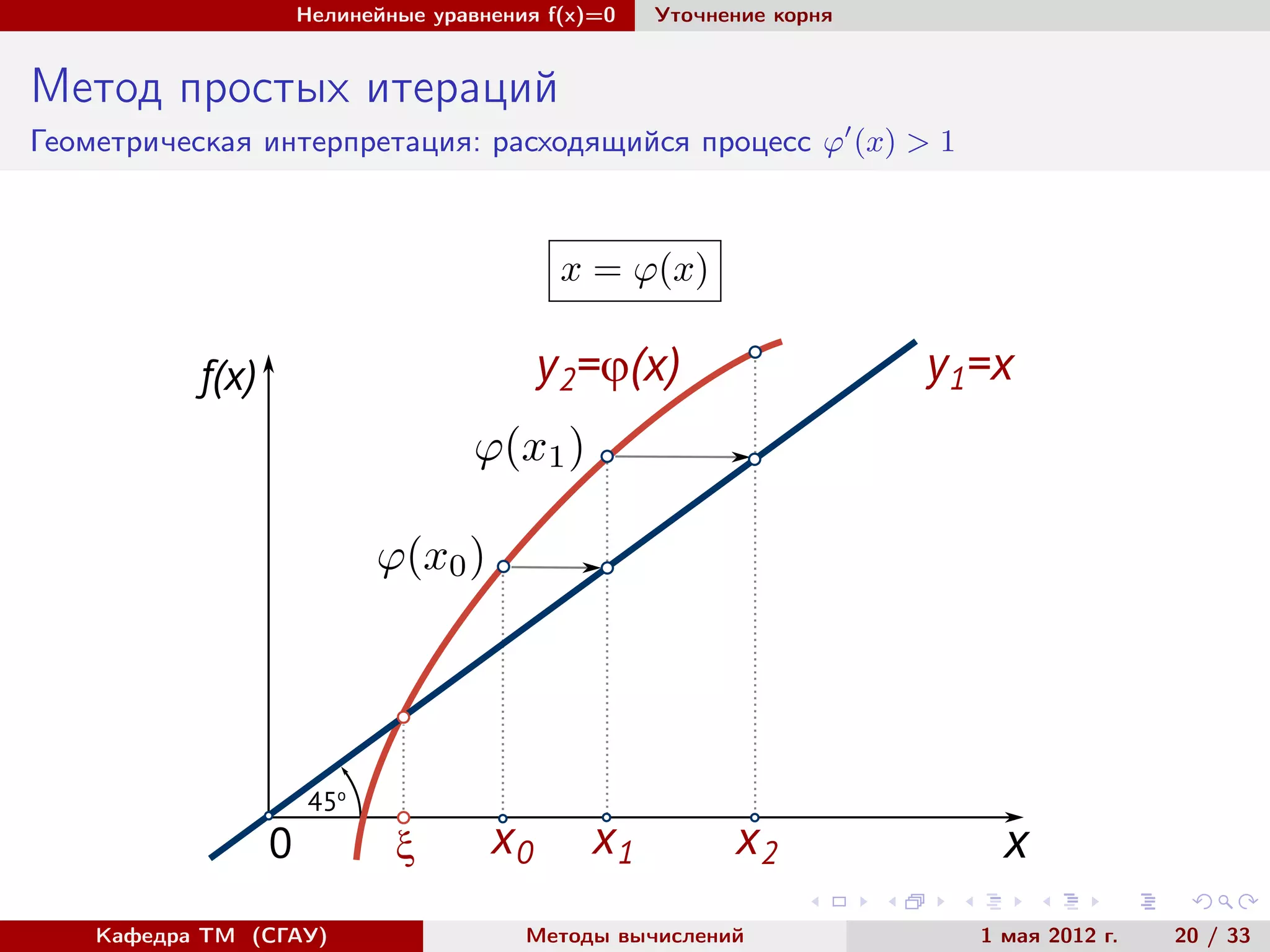
Метод простых итераций
Достаточное условие сходимости
Пусть функция ϕ(x) определена и дифференцируема на отрезке
x ∈ [a, b].
Если существует такое число q для которого на отрезке [a, b]
выполняется неравенство
|ϕ (x)| ≤ q < 1 (12)
то последовательность
xk+1 = ϕ(xk), k = 0, 1, 2, . . .
сходится к единственному корню уравнения x = ϕ(x) при любом
начальном приближении x0 ∈ [a, b]
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 18 / 33

19. Нелинейные уравнения f(x)=0 Уточнение корня
Метод простых итераций
Геометрическая интерпретация: сходящийся процесс, ϕ (x) < 1
x = ϕ(x)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 19 / 33

20. Нелинейные уравнения f(x)=0 Уточнение корня
Метод простых итераций
Геометрическая интерпретация: расходящийся процесс ϕ (x) > 1
x = ϕ(x)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 20 / 33

21. Нелинейные уравнения f(x)=0 Уточнение корня
Метод простых итераций
ϕ (x) > 1
Для случая ϕ (x) > 1 формируется эквивалентное уравнение
x = x ±
f(x)
max |f (x)|
(13)
”
-“ – для f (x) > 0
”
+“ – для f (x) < 0
Для эквивалентной функции
ϕ(x) = x ±
f(x)
max |f (x)|
(14)
производная меньше 1
ϕ (x) = 1 ±
f (x)
max |f (x)|
< 1 (15)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 21 / 33

22. Решение систем нелинейных уравнений
Решение систем нелинейных уравнений



F1(x1, x2, . . . , xn) = 0,
F2(x1, x2, . . . , xn) = 0,
. . .
Fn(x1, x2, . . . , xn) = 0,
(16)
Матричная форма
F(x) = ϑ (17)
где
F = [F1, F2, F3, . . . Fn]T
,
x = [x1, x2, x3, . . . xn]T
,
ϑ = [0, 0, 0, . . . , 0]T
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 22 / 33

23. Решение систем нелинейных уравнений Метод Зейделя
Метод Зейделя
Алгоритм
Исходная система уравнений записывается в эквивалентной форме



x1 = Φ1(x1, x2, . . . , xn),
x2 = Φ2(x1, x2, . . . , xn),
. . .
x2 = Φn(x1, x2, . . . , xn).
(18)
Пример построения эквивалентной функции Φi(x1, x2, . . . , xn):
Φi(x1, x2, . . . , xn) = xi + Fi(x1, x2, . . . , xn), i = 1, 2, . . . n
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 23 / 33

24. Решение систем нелинейных уравнений Метод Зейделя
Метод Зейделя
Алгоритм
Выбирается начальное приближение
x0
= [x
(0)
1 , x
(0)
1 , . . . , x(0)
n ]T
Выполняются итерации по следующей формуле
x
(k+1)
i = Φi(x
(k)
1 , x
(k)
1 , . . . , x(k)
n ) k = 1, n (19)
Вычисления (19) прекращают если достигнута заданная точность
||x(k+1)
− x(k)
|| ≤ ε
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 24 / 33

25. Решение систем нелинейных уравнений Метод Зейделя
Условие сходимости метода Зейделя
Метод Зейделя сходится к решению системы, если норма матрицы
Якоби
J(x(k)
) =
∂Φi(x)
∂xj x=xk
, i, j = 1, 2, . . . n (20)
меньше единицы
||J(x(k)
)|| < 1 (21)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 25 / 33

26. Решение систем нелинейных уравнений Метод Ньютона
Метод Ньютона
Строится итерационный процесс в следующем виде
x(k+1)
= x(k)
+ ∆x(k+1)
(22)
Для определения приращения ∆x(k+1) исходная система



F1(x2, x2, . . . , xn) = 0,
F2(x1, x2, . . . , xn) = 0,
. . .
Fn(x1, x2, . . . , xn) = 0,
заменяется на систему линейных уравнений относительно
приращений ∆x(k+1)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 26 / 33

27. Решение систем нелинейных уравнений Метод Ньютона
Метод Ньютона
Линеаризация уравнений
Функции Fi(x2, x2, . . . , xn) раскладываются в ряд в окрестности
x(k) с сохранение линейных относительно неизвестного вектора
∆x(k+1) слагаемых и найденное разложение приравнивается нулю:
Fi(x
(k+1)
1 , x
(k+1)
2 , . . . , x(k+1)
n ) = Fi(x
(k)
1 , x
(k)
2 , . . . , x(k)
n )+
+
∂Fi(x(k))
∂x1
∆x
(k)
1 +
∂Fi(x(k))
∂x2
∆x
(k)
2 + . . .
. . . +
∂Fi(x(k))
∂xn
∆x(k)
n = 0, i = 1, 2, . . . n (23)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 27 / 33

28. Решение систем нелинейных уравнений Метод Ньютона
Метод Ньютона
Система линейных уравнений для определения ∆x
(k)
1 , ∆x
(k)
2 , . . . ∆x
(k)
n
∂F1(x(k))
∂x1
∆x
(k)
1 +
∂F1(x(k))
∂x2
∆x
(k)
2 + . . . +
∂F1(x(k))
∂xn
∆x(k)
n = −F1(x(k)
)
∂F2(x(k))
∂x1
∆x
(k)
1 +
∂F2(x(k))
∂x2
∆x
(k)
2 + . . . +
∂F2(x(k))
∂xn
∆x(k)
n = −F2(x(k)
)
. . .
∂Fn(x(k))
∂x1
∆x
(k)
1 +
∂Fn(x(k))
∂x2
∆x
(k)
2 + . . . +
∂Fn(x(k))
∂xn
∆x(k)
n = −Fn(x(k)
)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 28 / 33

29. Решение систем нелинейных уравнений Метод Ньютона
Метод Ньютона
Система линейных уравнений
Чтобы система линейных алгебраических уравнений имела
единственное решение необходимо и достаточно, чтобы матрица Якоби
исходной системы была невырожденной
J(xk
) =




∂F1(x(k))
∂x1
. . . ∂F1(x(k))
∂xn
... . . .
...
∂Fn(x(k))
∂x1
. . . ∂Fn(x(k))
∂xn




det J(xk
) = 0
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 29 / 33

30. Решение систем нелинейных уравнений Метод Ньютона
Итерационный процесс
1 Матричная форма системы линейных уравнений для определения
приращения ∆x(k)
J(x(k)
)∆x(k)
= −F(x(k)
) (24)
x(k+1)
= x(k)
+ ∆x(k)
(25)
2 Вычисления (24), (25) продолжают пока
||x(k+1)
− x(k)
|| ≤ ε
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 30 / 33

31. Решение систем нелинейных уравнений Метод Ньютона
Задание 1
Найдите решение уравнения с точностью до 10−5:
f(x) = 2x cos 2x − (x − 2)2
= 0 (26)
на интервале [2; 3]
Для уточнения корня используйте метод половинного деления и
метод Ньютона, модифицированный метод Ньютона, метод хорд.
Сравните количество итераций, необходимых каждому методу для
уточнения решения до заданной точности.
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 31 / 33

32. Решение систем нелинейных уравнений Метод Ньютона
Задание 2
Найдите решение системы уравнений используя метод простых
итераций (метод Зейделя) и метод Ньютона с точностью 10−3:



3x1 − cos(x2x3) − 1
2 = 0
x2
1 − 81(x2 + 0.1)2 + sin x3 + 1.06 = 0
e−x1x2 + 20x3 + 10π−3
3 = 0
(27)
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 32 / 33

33. Решение систем нелинейных уравнений Метод Ньютона
Список использованных источников
1 Формалев В. Ф., Ревизников Д. Л. Численные методы, под. ред.
Кибзуна А. И. М.: Физматлит, 2004.
2 S. R. K Lyengar, R. K. Jain Numerical Methods, New Age
International (P) Limited, Publishers. 2009.
Кафедра ТМ (СГАУ) Методы вычислений 1 мая 2012 г. 33 / 33