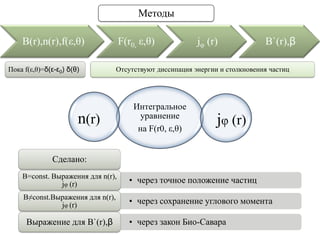
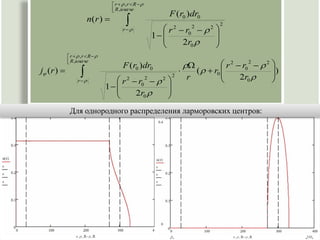
Документ описывает восстановление диамагнетизма частиц с большим ларморовским радиусом и методы вычисления распределения их плотности. Основное внимание уделяется вычислению интегральных уравнений и выражений для плотности частиц и угловых токов в различных магнитных полях. Рассматриваются условия, при которых частицы могут быть абсорбированы и влияние симметрии поля на их траектории.

1. Восстановление диамагнетизма частиц с большим
Ларморовским радиусом по распределению их плотности
Выполнил:
Палкин Егор
7302
Научный
руководитель:
Беклемишев
А.Д.

2. Методы
B(r),n(r),f(ε,θ) F(r0, ε,θ) jφ (r) B`(r),β
Пока f(ε,θ)=δ(ε-ε0) δ(θ) Отсутствуют диссипация энергии и столкновения частиц
Интегральное
уравнение
n(r) на F(r0, ε,θ)
jφ (r)
Сделано:
B=const. Выражения для n(r),
jφ (r) • через точное положение частиц
B≠const.Выражения для n(r),
jφ (r) • через сохранение углового момента
Выражение для B`(r),β • через закон Био-Савара

3. B=(0,0,B)=const.
Введѐм r0 :радиальный вектор ларморовского центра частицы.
2 2 T
1   
n(r )   F (r0 )  d  d0   (r  r0   (t ))d  (t )
T 0 0 0
Только частицы, траектории
которых проходят через кольцо
усреднения дают вклад в
интеграл.
• При данном r максимально
далѐкая точка дающая вклад в
интеграл r0+ρ, и минимальная
r0-ρ.
• Будем считать, если частица
выходит за радиус R, то она
пропадает(абсорбция)
Для jφ отличие в множителе evφ

4.  r   ,r  R  
 R ,иначе

F (r0 )dr0
n( r )   2
r  r 2  r0 2   2 
1 



 2r0  
 r   ,r  R  
 R ,иначе

F (r0 )dr0   r 2  r0 2   2 
j (r )   2

r
(   r0 

 2r0 
)


r  r 2  r0 2   2 

1  
2r0  
 
Для однородного распределения ларморовских центров:

5. B=(0,0,B(r))
В аксиально симметричном магнитном поле траектория частицы не может считаться
окружностью, также усложняется понятие r0, ρ.
dT
dN   F (0 )d0 1 dT 1
2r 
T  n( r )  F (0 )d0
dr T
dN  n2rdr
При правильной калибровке векторного потенциала из Лагранжевого подхода можно
найти vφ , а используя закон сохранения энергии: vr . Выберем r+ как новую
параметризацию. r+ и r- определяются из интеграла движения pφ.
Уравнение для r+ и r- :
p
 const   r  A(r )r  r  A(r )r
mvtr

6. Модельное поле и вектор - Область определения ядра
потенциал: интегрального оператора
B(r )
D
A(r )
(r , r , r ) F (r )dr
2
1
n( r )  
r while r
r  r  r vtr 1  {  [A(r )  1]  A(r )}2
r