This document discusses square numbers and properties related to square roots. It includes: - A chart of perfect square numbers from 1 to 30 - Explanations of how to find a square number and what qualifies as a perfect versus non-perfect square - Information about Pythagoras' theorem that the square of the hypotenuse of a right triangle equals the sum of the squares of the other two sides - An example of finding a Pythagorean triplet using the formula (2m^2) + (m^2 - 1) = (m^2 + 1) - A method for finding square roots through repeated subtraction to get a remaining value of 0 - 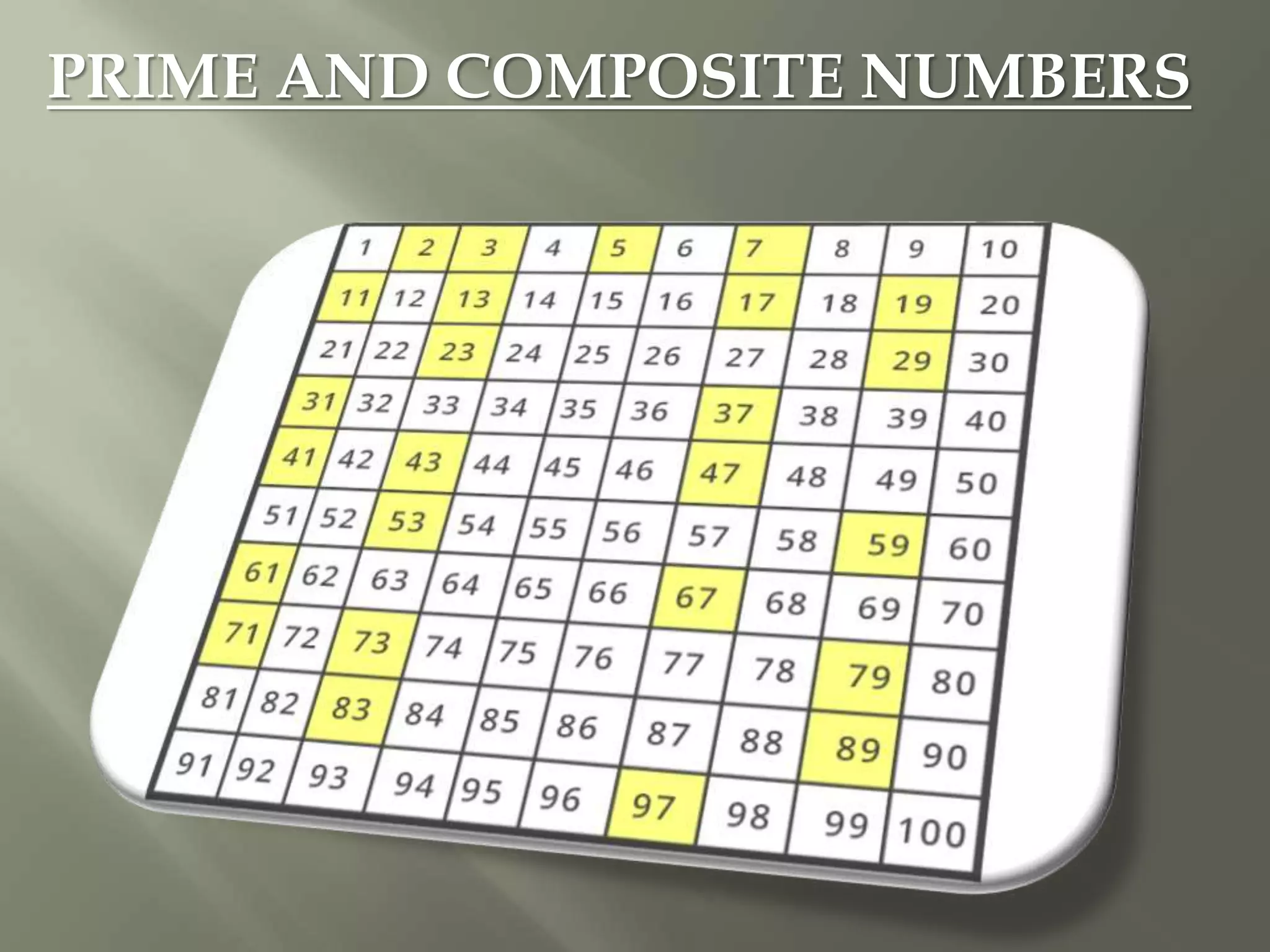Brief definitions of prime and

1. NAME – RAJVEER JAIN
CLASS – 8B
SUBJECT - MATHS

2. SQUARE ROOT
CHART OF PERFECT SQUARE 1 TO 30

3. HOW TO FIND A SQUARE?
You get a square number by multiplying a number by itself, so
knowing the square numbers is a handy way to remember part
of the multiplication table. Although you probably remember
without help that 2*2 = 4, you may be sketchy on some of the
higher numbers, such as 7*7 = 49. Knowing the square numbers
gives you another way to etch that multiplication table forever
into your brain.

4. PERFECT AND NON – PERFECT
SQUARE
If a number ends with 2 , 4 , 7 and 8 at units place. So, Its may be
a non – perfect square.
EXAMPLE – 138, 42, 87, ETC.
If a number ends with 0 , 3 , 5 , 6 and 9 at units place. So, Its may
be a perfect square.
EXAMPLE – 133, 40, 89, ETC.
EXAMPLE : i) 16 (YES) 16 = 4 × 4
ii) 28 (NO) As it ends with 8.

5. PYTHAGORAS THEORAM
A square of a number is equal to a sum of a two square
numbers. This property is called Pythagoras property and the
three number use in this property are called Pythagoras
theorem.
FORMULA = A2 + B2 = C2
52= 32 + 42
25 = 9 + 16
25 = 25

6. PYTHAGORAS TRYPLET
The formula of finding more such Tryplet is
( 2m2 ) + ( m2 – 1 ) = ( m2 + 1 )
EXAMPLE – Pythagoras Tryplet whose smallest number is 12.
1) 2m = 12 2) m2 – 1 3)m2 + 1
m = 12/2 62 – 1 62 + 1
m = 6 36 – 1 36 + 1
35 37
CHECK : 122 + 352 = 372
144 + 1225 = 1369
1369 = 1369
So, 12, 35 or 37 are
Pythagoras Tryplet.

7. FINDING THE SQUARE ROOTS
REPEATED SUBTRACTON
The subtraction of odd consequently to the number still we get
0. So, the number of observation we subtract to the number is
the square root of that number
Finding square root of 64.
1) 64 – 1 = 63
2) 63 – 3 = 60
3) 60 - 5 = 55
4) 55 – 7 = 48
5) 48 – 9 = 39
6) 39 – 11 = 28
7) 28 – 13 = 15
8) 15 – 15 = 0
= 82
SO THE SQUARE ROOT
OF 64 IS 8.

8. PRIME AND COMPOSITE NUMBERS

9. PRIME FACTORISATION
2 256
2 128
2 64
2 32
2 16
2 8
2 4
2 1
256 = 2 × 2 × 2 × 2 × 2 × 2 ×
2 × 2
256 = 2 × 2 × 2 × 2
256 = 16

10. PROPERTY OF UNIT DIGIT OF
SQUARE ROOT
1)1
2)9
3)2
4)8
If a square number has 1 or 9 at units place then its
square also end with 1
If a square number has 2 or 8 at units place
then its square also end with 4.