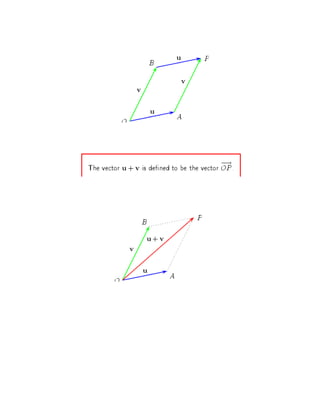
There are two methods for adding vectors: the parallelogram rule and the triangle rule. The parallelogram rule involves translating the vectors tail-to-tail to form the sides of a parallelogram, where the diagonal lines represent the sum vector. The triangle rule places the tail of one vector at the head of the other to form a triangle, where the third side of the triangle is the sum vector. Both methods are equivalent and result in the sum vector having the same magnitude and direction regardless of the order of the original vectors.

1. Appendix 1
DETERMINING THE RESULTANT VECTOR OF TWO VECTORS
Because non-zero vectors have direction as well as magnitude, adding vectors involves more
than simply adding numbers. The sum of two vectors is another vector, and so the definition of
addition must give a process for determining both the magnitude and the direction of the sum
vector. There are two equivalent procedures for addition of vectors, called the parallelogram rule
and the triangle rule.
The parallelogram rule for addition
Suppose u and v are two vectors. Translate them so that they are tail-to-tail at point O.
uuu uuu
r r
From the head of each vector, draw r copyrof the other vector to complete a parallelogram
uuua uuu
OAPB. In this parallelogram, u = OA = BP and v = OB = AP
.

3. The triangle rule for addition
This way defines addition of two vectors is by a head-to-tail construction that creates two sides
of a triangle. The third side of the triangle determines the sum of the two vectors, as shown
below.
uuu
r uuu
r
Place the tail of the vector v at the head of the vector u. That is, u = OA and v = .
AP
uuu
r
Now construct the vector OP to complete the third side of the triangle OAP.
This method is equivalent to the parallelogram law of addition, as can be easily seen by drawing
a copy of v tail-to-tail with u, to obtain the same parallelogram as before.

4. Using position vector notation, the triangle rule of addition is written as follows: for any three
points X, Y , Z,
Both the triangle and the parallelogram rules of addition are procedures that are independent of
the order of the vectors; that is, using either rule, it is always true that u + v = v + u for all
vectors u and v. This is known as the commutative law of addition.