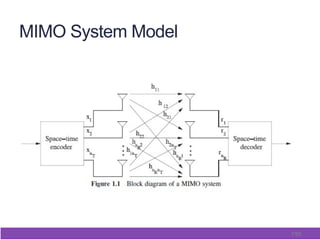
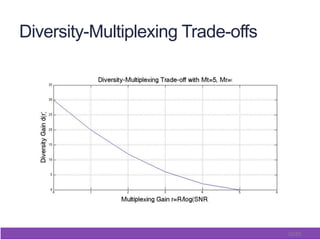
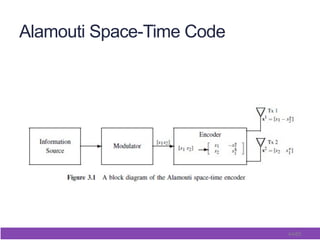
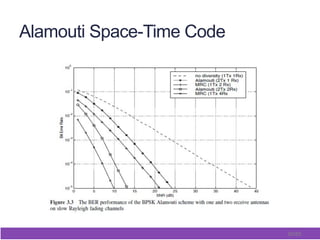
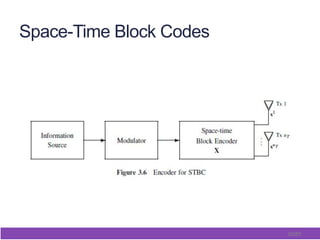
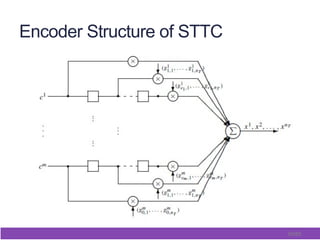
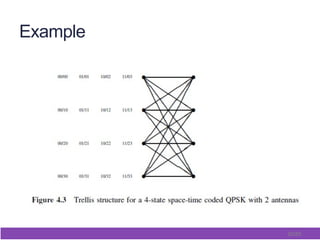
This document outlines and describes space-time coding techniques for MIMO wireless systems. It introduces MIMO system models and derives MIMO capacity. It then discusses space-time coding performance analysis, including diversity-multiplexing tradeoffs and error analysis. Finally, it describes specific space-time coding schemes, including Alamouti codes, space-time block codes, and space-time trellis codes.

1. 1/65
SPACE TIME CODING
Jie Ren
ASPITRG Drexel

2. 2/65
• B. Vucetic and J. Yuan, Space-Time Coding, Wiley, 2003
• Erik G. Larsson and Petre Stoica Space-Time Block
Coding for Wireless Communications, Cambridge, 2005

3. 3/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes

4. 4/65
Outline
• MIMO Wireless Communication Systems
o MIMO System Model
o MIMO System Capacity Derivation
o MIMO Capacity Examples
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes

5. 5/65
Outline
• MIMO Wireless Communication Systems
o MIMO System Model
o MIMO System Capacity Derivation
o MIMO Capacity Examples
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes

6. 6/65
MIMO System Model
• Notations
nT transmit antennas
nR receive antennas
x transmitted signals, N(0,µ) i.i.d.
n noise
r received signals
Rxx, Rnn, Rrr covariance matrix of x, n and r

7. 7/65
MIMO System Model

8. 8/65
MIMO System Model
• Covariance matrix of the transmitted signal
• Transmitted power constraint
• Channel is unknown at the transmitter

9. 9/65
MIMO System Model
• Noise n
• independent complex zero-mean Gaussian
• No correlation between components of n

10. 10/65
MIMO System Model
• MIMO Channel H
• nR by nT complex matrix
• perfectly known at the receiver
• not known at the transmitter
• normalization:

11. 11/65
MIMO System Model
• Average SNR at each receive antenna
• Received vector
! =
!!
!! =
!
!!!

12. 12/65
Outline
• MIMO Wireless Communication Systems
o MIMO System Model
o MIMO System Capacity Derivation
o MIMO Capacity Examples
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes

13. 13/65
MIMO System Capacity Derivation
• Theorem: Singular value decomposition
• Suppose M is an m×n matrix whose entries come from the field K.
(either the field of real numbers or the field of complex numbers)
Then,
• where U is an m×m unitary matrix over K, V* is the conjugate
transpose of the n×n unitary matrix V over K, Σ is an m×n diagonal
matrix with non-negative real numbers on the diagonal.
! = !!!!!
!

14. 14/65
MIMO System Capacity Derivation
• Singular value decomposition
! = !"!!!
! = !"!!! + !!
!!! = !!!"!!! + !!! = ! !!! + !!!!
!
!

15. 15/65
MIMO System Capacity Derivation
• Singular value decomposition
• Equivalent channel

16. 16/65
MIMO System Capacity Derivation
• Singular value decomposition
• Equivalent channel

17. 17/65
MIMO System Capacity Derivation
• Covariance Matrix
• Power constraint

18. 18/65
MIMO System Capacity Derivation
• Capacity

19. 19/65
MIMO System Capacity Derivation
• Capacity: Relates to the channel matrix H
! =
!!!, !! < !!
!!!, !! ≥ !!
!
! − !! = det!(!!! − !)
!
!!!
!
!"#!$%$"$&!! = −
!!!!
!
!
! = ! log! det!(!! +
!
!!!! !)!

20. 20/65
Outline
• MIMO Wireless Communication Systems
o MIMO System Model
o MIMO System Capacity Derivation
o MIMO Capacity Examples
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes

21. 21/65
Examples 1
• SISO channel
• 1 receive antennas and 1 transmit antennas

22. 22/65
Examples 2
• MIMO channel with unity H
• Coherent combining
• Reduces to a single effective channel

23. 23/65
Example 3
• Receive Diversity
• n receive antennas and 1 transmit antennas

24. 24/65
Example 4
• Transmit Diversity
• n transmit antennas and 1 receive antennas

25. 25/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes

26. 26/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
o Diversity-Multiplexing Tradeoff
o ML Detection
o Error Analysis
o Space-Time Code Design Criteria
• Space-Time Block Codes
• Space-Time Trellis Codes

27. 27/65
Diversity-Multiplexing Tradeoff
• Why MIMO?
• Utilize multiple antennas to improve wireless system performance
• Higher capacity
• Lower error probability

28. 28/65
Definitions
• Diversity Gain d
• Change in slope of the error probability
• Multiplexing Gain r
• Change in slope of the rate

29. 29/65
Beamforming
• Antennas transmit the same signal
• Pre-coding and shaping matrices (vectors): u, v
• Corresponding SNR

30. 30/65
Diversity-Multiplexing Trade-offs
• Obtain full multiplexing gain
• Decompose the MIMO into parallel SISO
• multiplexing different data streams
• each SISO quality depends on the singular values of HHH
• may have poor performance
• Obtain full diversity gain
• Apply beamforming

31. 31/65
Diversity-Multiplexing Trade-offs
• Fundamental design question:
• Should the antennas be used for diversity gain, multiplexing gain or
both?
• Assume block fading channels with receiver CSI only
• Maximum d for fixed r:

32. 32/65
Diversity-Multiplexing Trade-offs

33. 33/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
o Diversity-Multiplexing Tradeoff
o ML Detection
o Error Analysis
o Space-Time Code Design Criteria
• Space-Time Block Codes
• Space-Time Trellis Codes

34. 34/65
Space-Time Coded Systems
• Information symbols
• Input vector
• Received vector

35. 35/65
ML Detection
! = argmin
!∈!!!×!
||! − !"||!
!
= arg min ||!! − !!!||!
!
!!!
!

36. 36/65
Space-Time Coded Systems
• Decision Metrics
• Selects a code word with the minimum decision metric

37. 37/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
o Diversity-Multiplexing Tradeoff
o ML Detection
o Error Analysis
o Space-Time Code Design Criteria
• Space-Time Block Codes
• Space-Time Trellis Codes

38. 38/65
Error Analysis
• AWGN fading channel
• General error probability
!! = ! ∙ !( ! ∙
!!
!!
)!
!!
= !!
! = |!|!
!
!
ℎ~!!(!, !)!

39. 39/65
Error Analysis
• Theorem: The error probability, averaged over h, is
bounded by:

40. 40/65
Error Analysis
• Diversity gain: Gd
• Coding gain: Gc

41. 41/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
o Diversity-Mutiplexing Tradeoff
o ML Detection
o Error Analysis
o Space-Time Code Design Criteria
• Space-Time Block Codes
• Space-Time Trellis Codes

42. 42/65
Space-Time Code Design Criteria
• Pair-wise error probability for STC
• Rank criterion: the difference matrix must be full rank to obtain the
maximum diversity gain MrMt
• Determinant criterion: maximize the minimum of the Det(Δ) to
obtain a high coding gain

43. 43/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Alamouti’s Space-Time Code
• STBC
• Space-Time Trellis Codes

44. 44/65
Alamouti Space-Time Code

45. 45/65
Alamouti Space-Time Code
• Orthogonal Property
• Received Signal

46. 46/65
Alamouti Space-Time Code
• Define
• where e is white noise

47. 47/65
Alamouti Space-Time Code
• ML detection

48. 48/65
Alamouti Space-Time Code
• Decision Statistics
• Decision Rules

49. 49/65
Alamouti Space-Time Code
• Achieve a full diversity gain

50. 50/65
Alamouti Space-Time Code

51. 51/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Alamouti’s Space-Time Code
• STBC
• Space-Time Trellis Codes

52. 52/65
Space-Time Block Codes

53. 53/65
Space-Time Block Codes
• Code Matrix
• Orthogonal Property

54. 54/65
Decoding of STBC
• Decision Statistics
• Decision Rules

55. 55/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes
o Delay Diversity Code
o General STTC

56. 56/65
Delay Diversity
• STTC: a steam of data is encoded via Nt convolutional
encoders
• Delay Diversity for Nt=2
• First convolutional encoder: absent
• Second convolutional encoder: replace by time delay

57. 57/65
Delay Diversity
• covariance matrix of he full rank

58. 58/65
Outline
• MIMO Wireless Communication Systems
• Space-Time Coding Performance Analysis
• Space-Time Block Codes
• Space-Time Trellis Codes
o Delay Diversity Code
o General STTC

59. 59/65
Encoder Structure of STTC

60. 60/65
Encoder Structure of STTC
• Generator Description
• Generator Polynomial Description

61. 61/65
Example
• 4-state space-time trellis coded QPSK scheme with 2
transmit antennas
• Generator sequences:

62. 62/65
Example

63. 63/65
Decoder Structure of STTC
• Maximum Likelihood Decoding
• Employ Viterbi Algorithm
• Minimize the path metric