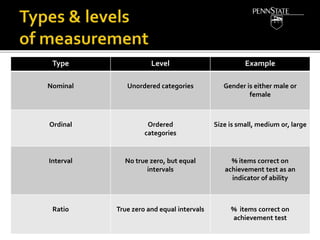
This document discusses statistical concepts and measurement, types of variables, and key terms for data analysis. It addresses: - How variables are measured and the levels of measurement (nominal, ordinal, interval, ratio). - The difference between discrete and continuous variables. - Key terms like population, sample, parameter, and statistic and how inferences are made about populations based on statistics from samples. 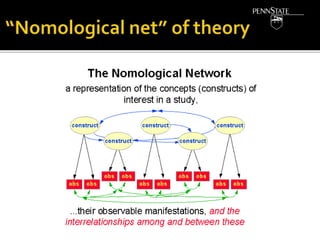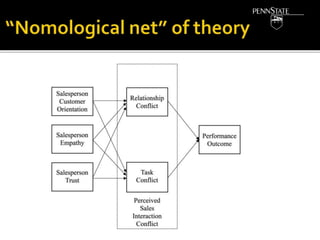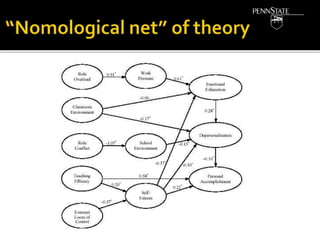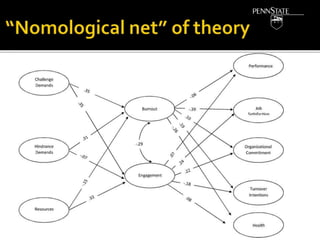- The components of theories, including propositions, nomological networks, and hypotheses testing. - Important sources for PhD students, including familiarity with key concepts and links to additional documents.

1. DATA ANALYSIS
12 November 2018

2. How is a variable measured?
Some statistical concepts
What is a theory?
Some important sources for PhD students

4. An entity that has two or more mutually
exclusive values

5. Measurement is a process of assigning values
to variables based on rules
Measurement results from an interaction
among an instrument, the subject being
measured, and the measurement
environment

6. Type Level Example
Nominal Unordered categories Gender is either male or
female
Ordinal Ordered
categories
Size is small, medium or, large
Interval No true zero, but equal
intervals
% items correct on
achievement test as an
indicator of ability
Ratio True zero and equal intervals % items correct on
achievement test

7.  Discrete –
• Well-defined finite set of possible values (which are
called states of the discrete variable).
• Commonly have 9 or fewer categories with numeric
values, but can have more (e.g., country names)
 Continuous –
• Take on any value between any other two values.
• Any real-values number along a number line.
• Usually even variables with discrete values are treated
as continuous if they have >9 values.

8. Measurement Levels
Nominal Ordinal Interval Ratio
TypesofVariables
Discrete
X X
Maybe, but
treated as
continuous
Maybe, but
treated as
continuous
Continuous Never Never
X X

9. TERMS, DEFINITIONS,AND APPROACH

10.  Population versus sample
 Parameter versus statistic
 Inference of population parameters from
sample statistics

11.  Population
• Any complete group with at least one characteristic in
common
• Not just people, but any entity
• Might consist of, but not limited to, people, animals,
businesses, buildings, motor vehicles, farms, objects, or
events
 Sample
• A group of units selected from a larger group (the
population)
• Generally selected for study because the population is too
large to study in its entirety
• Good samples represent the population

12.  Parameter
• Information about a population
• Characteristic of a population
• A population value
• The “truth”
 Statistic
• Information about a sample
• An estimate of a population value

13. POPULATION
SAMPLE
represents
The sample represents
the population

14. POPULATION
SAMPLE
Drawn from
The sample drawn
from the population

15. PARAMETER
STATISTIC
A population
parameter is inferred
from a statistic

16. PARAMETER
STATISTIC
is used to infer
A population
parameter is inferred
from a statistic

17. PARAMETER
STATISTIC
estimates
A statistic is used to
estimate a population
parameter

18. POPULATION
SAMPLE
PARAMETER
STATISTIC
A parameter is a
characteristic of a
population

19. POPULATION
SAMPLE
PARAMETER
STATISTIC
A statistic calculated
from a sample
estimates a parameter
from a population
estimates

20.  Data usually are available from a sample, not a
population
 That is, sample statistics are available, not population
parameters
 We wish to infer (or estimate) parameters from
statistics
 Because data are available from a sample, not the
population, error occurs when inferring (or estimating)
population parameters from sample statistics
 Statistical techniques help us make decisions under
error and uncertainty

21. THEORY, PROPOSITIONS, LOGIC

22.  Are composed of propositions that explain the
empirical, observable world. A proposition is an
“if–then” statement
 Are networks showing relationship and causality
among propositions
 Must have“empirical import”

23.  The foundation of theory-building
 Statements of testable scientific propositions
 The focus for empirical work

24.  Examine propositions in theory that require
verification.
 Are specific.
 Are testable.

25. The term "nomological" is derived from Greek
and means "lawful”
A nomological network is a "lawful network,” a
network of propositions that describe how
things work

30.  Hypotheses are“tested”
 Hypotheses are never“proved”
 Hypotheses only are“rejected”
 Theories are built and verified by testing hypotheses

31. — FAMILIARITY ESSENTIAL FOR PhD STUDENTS
— LINKSTO DOCUMENTSON PIAZZA

32.  Good (not easy)
explanation in Ch 1 +
Ch 2

34. DATA ANALYSIS
12 November 2018