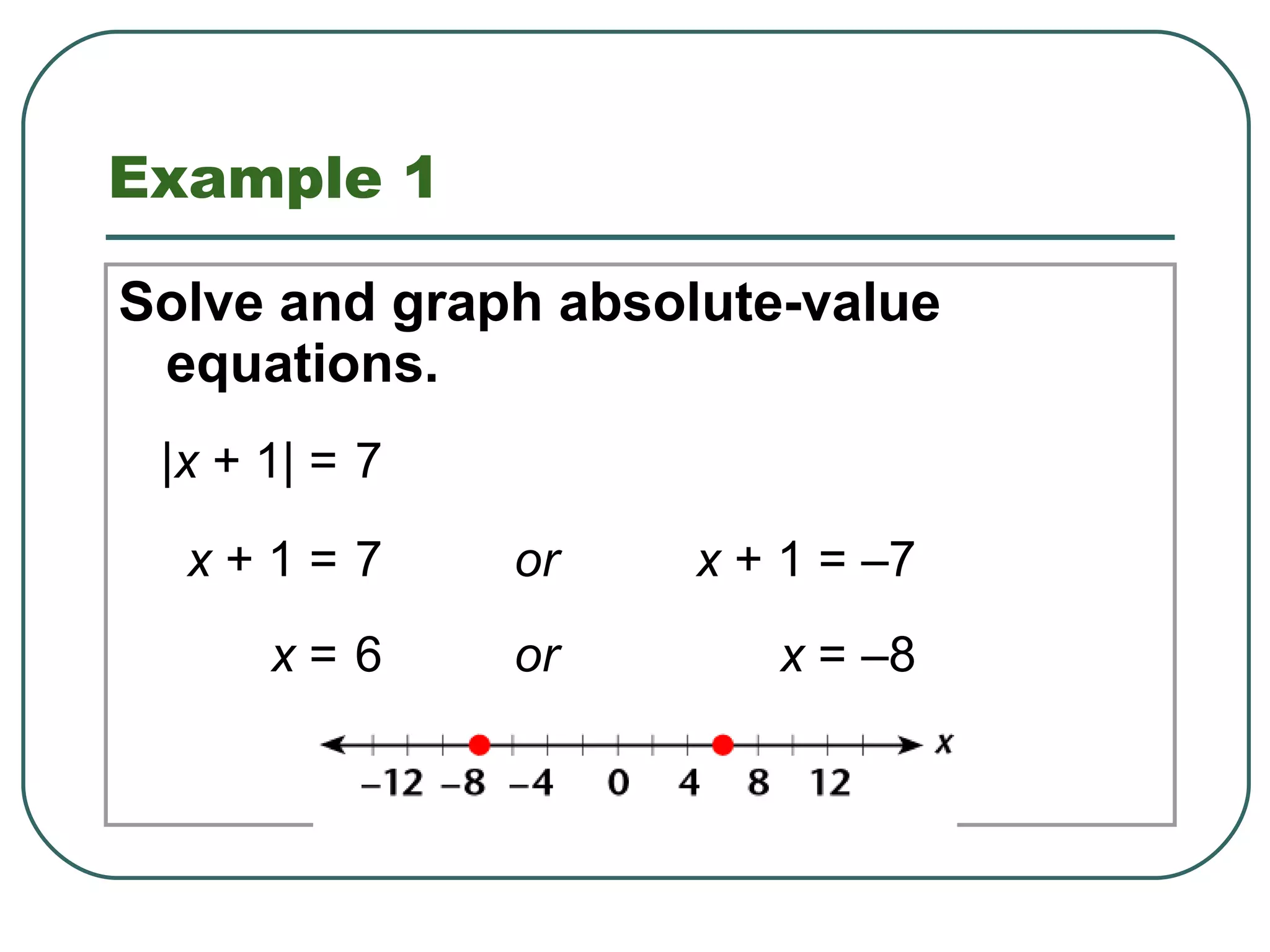
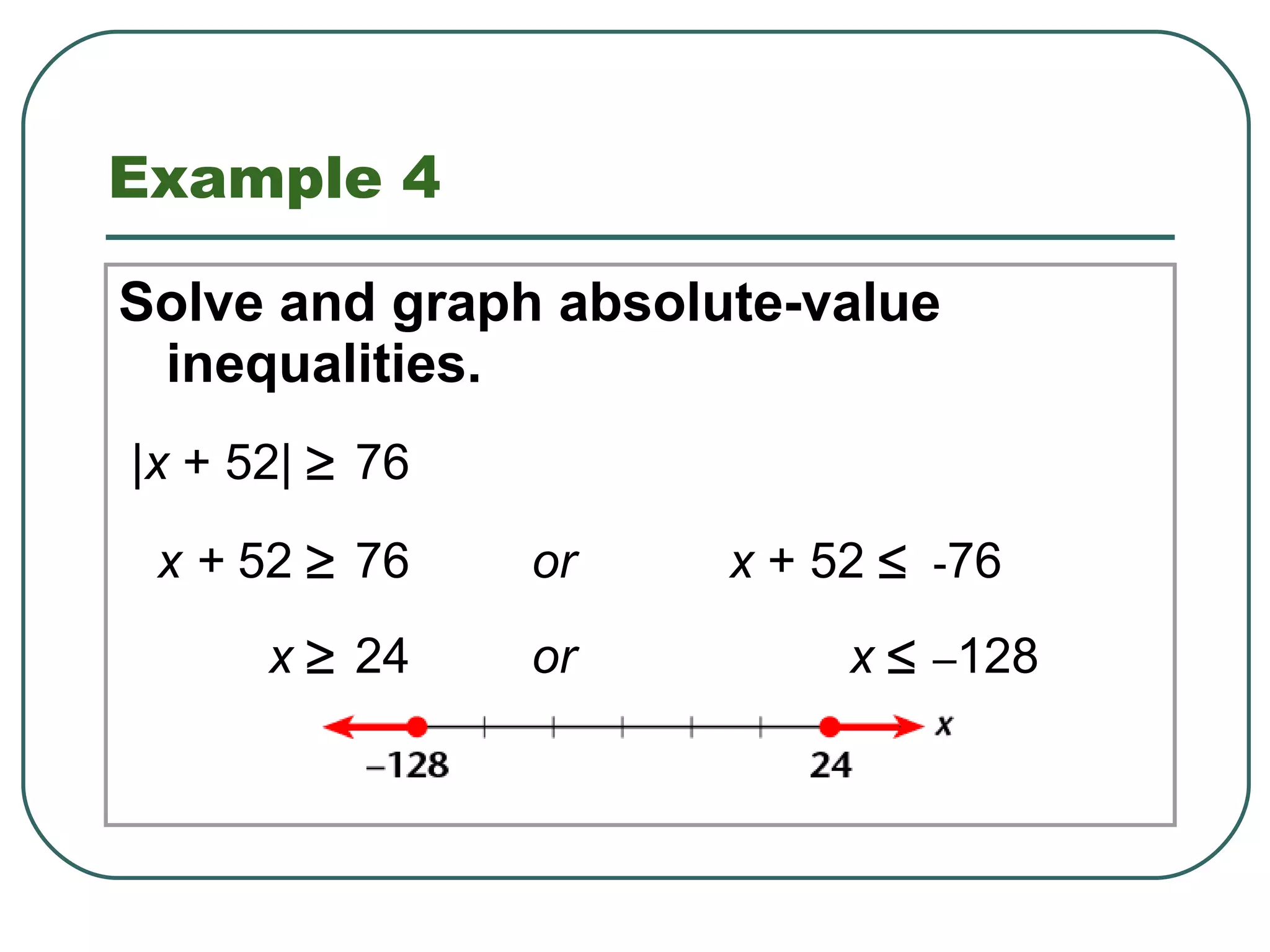
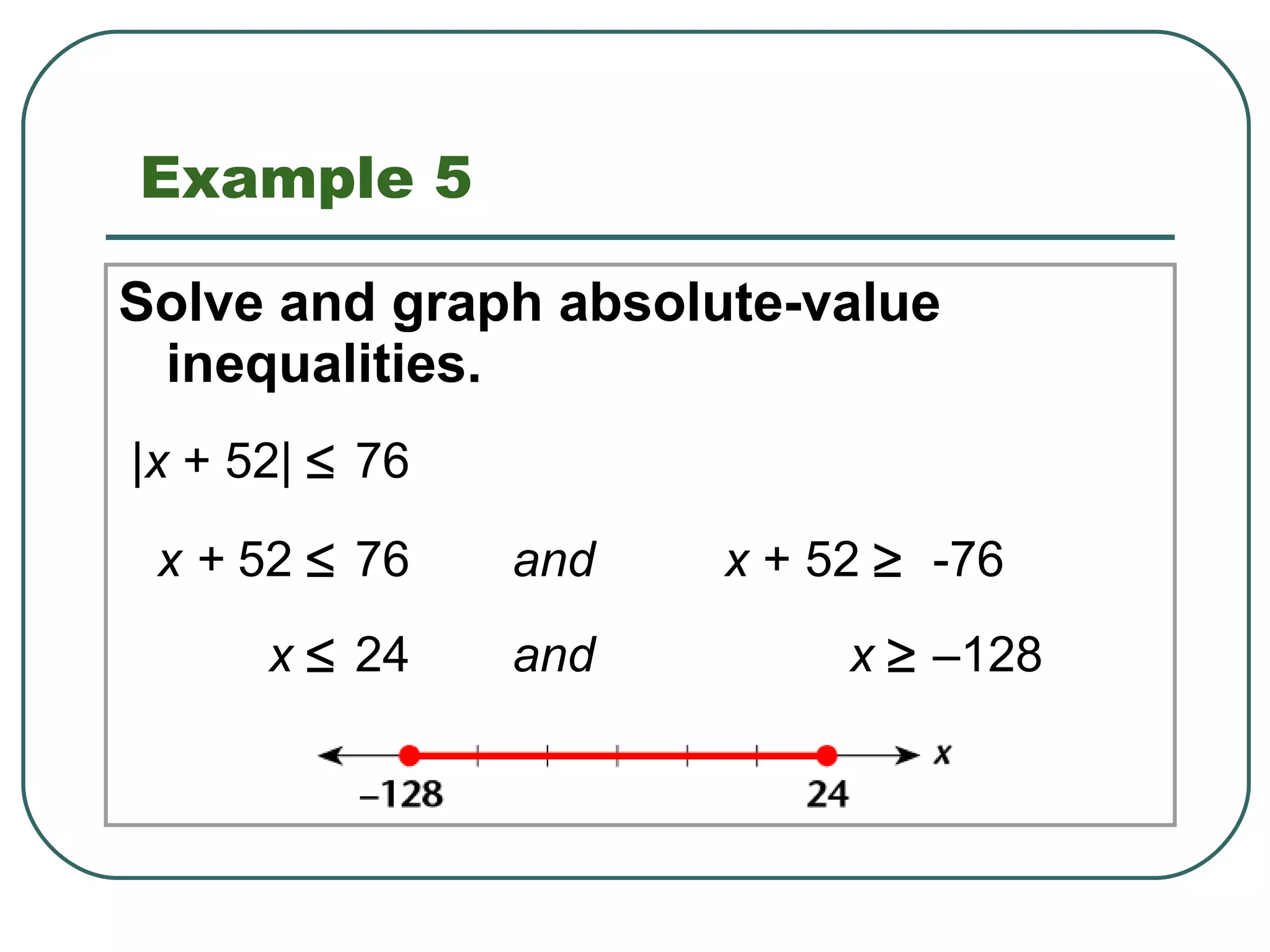
This document discusses rules and properties for solving absolute value equations and inequalities. It states that if a is greater than 0 and the absolute value of x is equal to a, then x equals a or negative a. If the absolute value of x is less than a, x is between negative a and a. If the absolute value of x is greater than a, x is less than negative a or greater than a. It provides examples of solving different types of absolute value equations and inequalities.

1. Absolute Value

2. Absolute Value

3. Rules and Properties Absolute-Value Equations If a > 0 and | x | = a , then x = a or x = – a . 1.8 Solving Absolute-Value Equations and Inequalities Absolute-Value Inequalities If a > 0 and | x | < a , then x > – a and x < a . If a > 0 and | x | > a , then x < – a or x > a . Similar statements are true for | x |  a and | x |  a.

4. Absolute Value Rules If you start with an “=“ sign then you will have an “or” statement. If you start with a “<“ or a “ ≤” then you will have an “and” statement. If you start with a “>” or a “≥” then you will have an “or” statement.

5. Example 1 Solve and graph absolute-value equations. | x + 1| = 7 1.8 Solving Absolute-Value Equations and Inequalities

6. Example 1 Solve and graph absolute-value equations. | x + 1| = 7 1.8 Solving Absolute-Value Equations and Inequalities x + 1 = 7 or x + 1 = –7 x = 6 or x = –8

7. Example 2 Solve and graph absolute-value equations. 4| x | = 8 1.8 Solving Absolute-Value Equations and Inequalities

8. Example 2 Solve and graph absolute-value equations. 4| x | = 8 1.8 Solving Absolute-Value Equations and Inequalities 4 x = 8 or 4 x = –8 x = 2 or x = –2

9. Example 3 |x - 4| = x + 1

10. Example 3 |x - 4| = x + 1 x = x + 5 or x – 4 = -x - 1 0 = 5 or 2x – 4 = -1 x - 4 = x + 1 x - 4 = -(x + 1) No Solution or 2x = 3 No Solution or x = 3/2 3/2

11. Example 4 Solve and graph absolute-value inequalities. | x + 52|  76 1.8 Solving Absolute-Value Equations and Inequalities

12. Example 4 Solve and graph absolute-value inequalities. | x + 52|  76 x + 52  76 or x + 52  - 76 x  24 or x  – 128 1.8 Solving Absolute-Value Equations and Inequalities

13. Example 5 Solve and graph absolute-value inequalities. | x + 52|  76 1.8 Solving Absolute-Value Equations and Inequalities

14. Example 5 Solve and graph absolute-value inequalities. | x + 52|  76 x + 52  76 and x + 52  -76 x  24 and x  –128 1.8 Solving Absolute-Value Equations and Inequalities