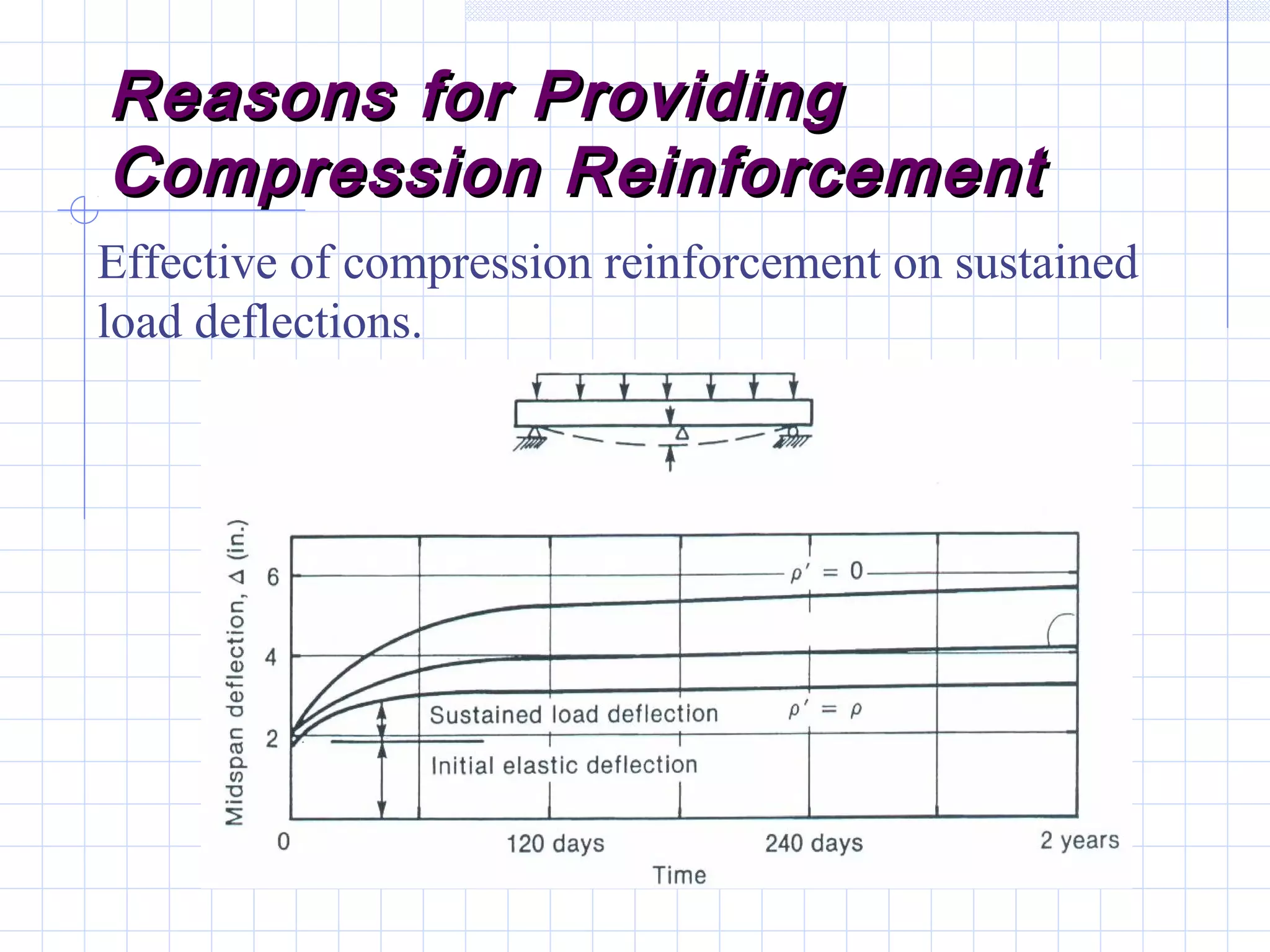
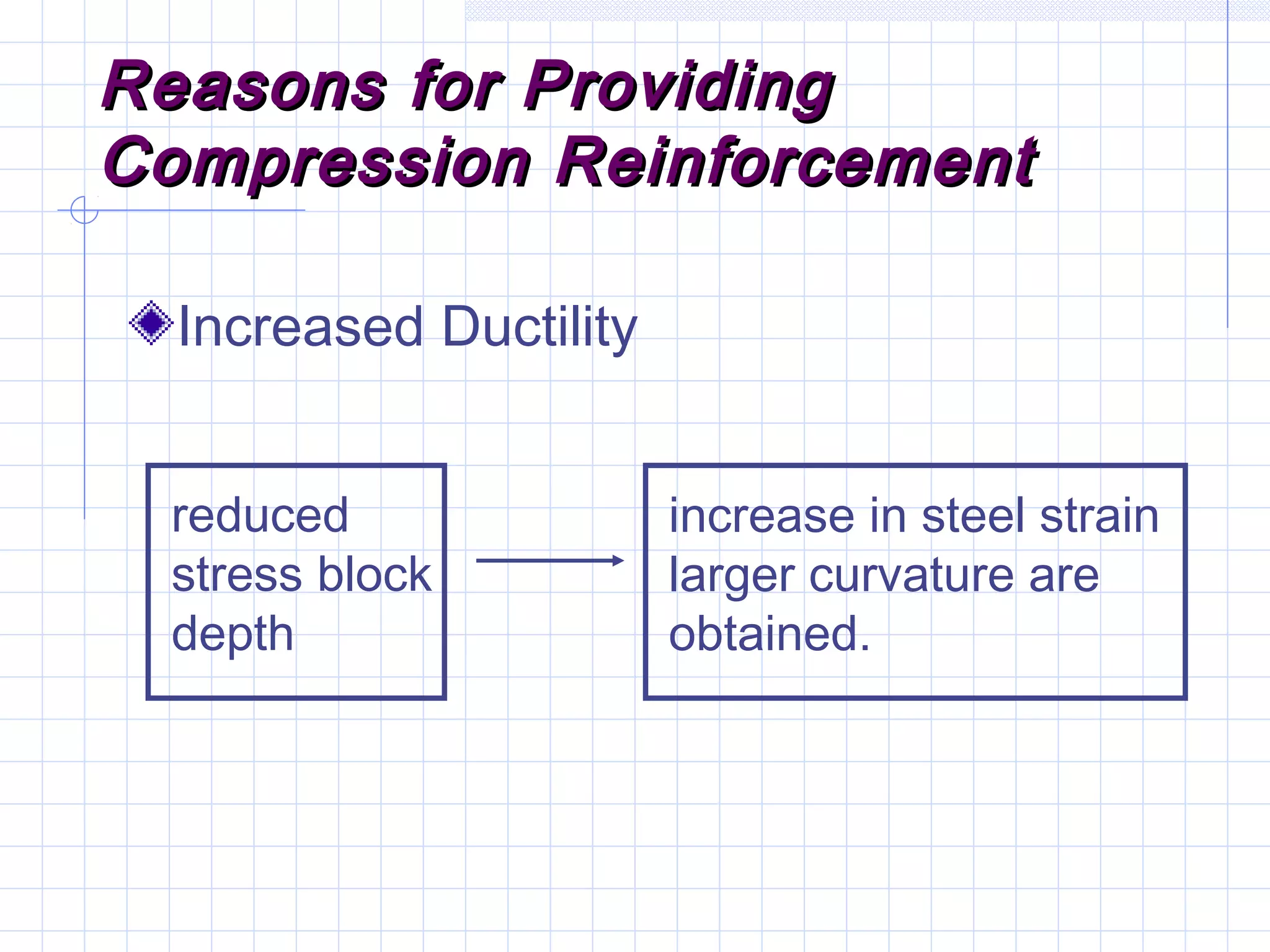
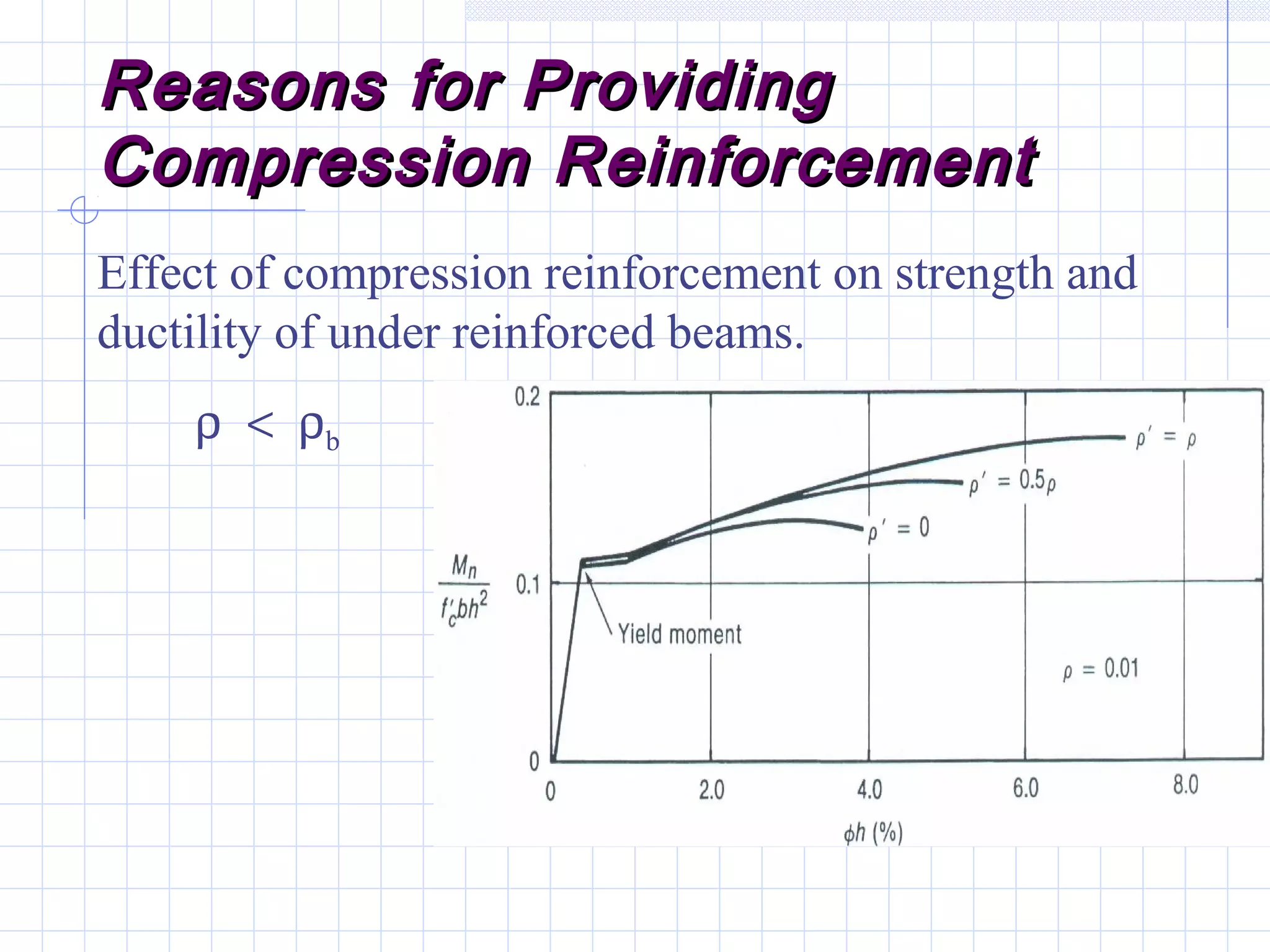
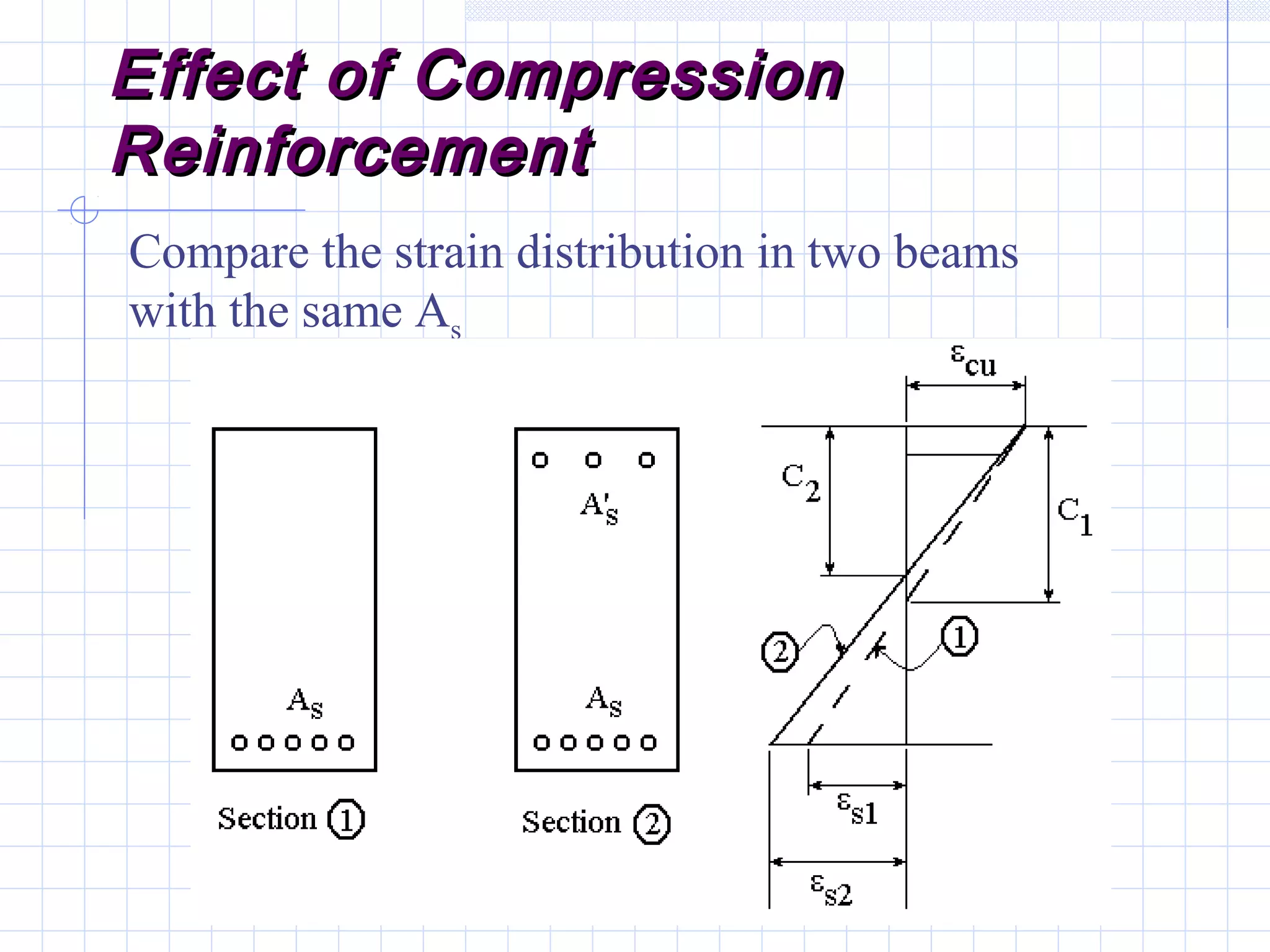
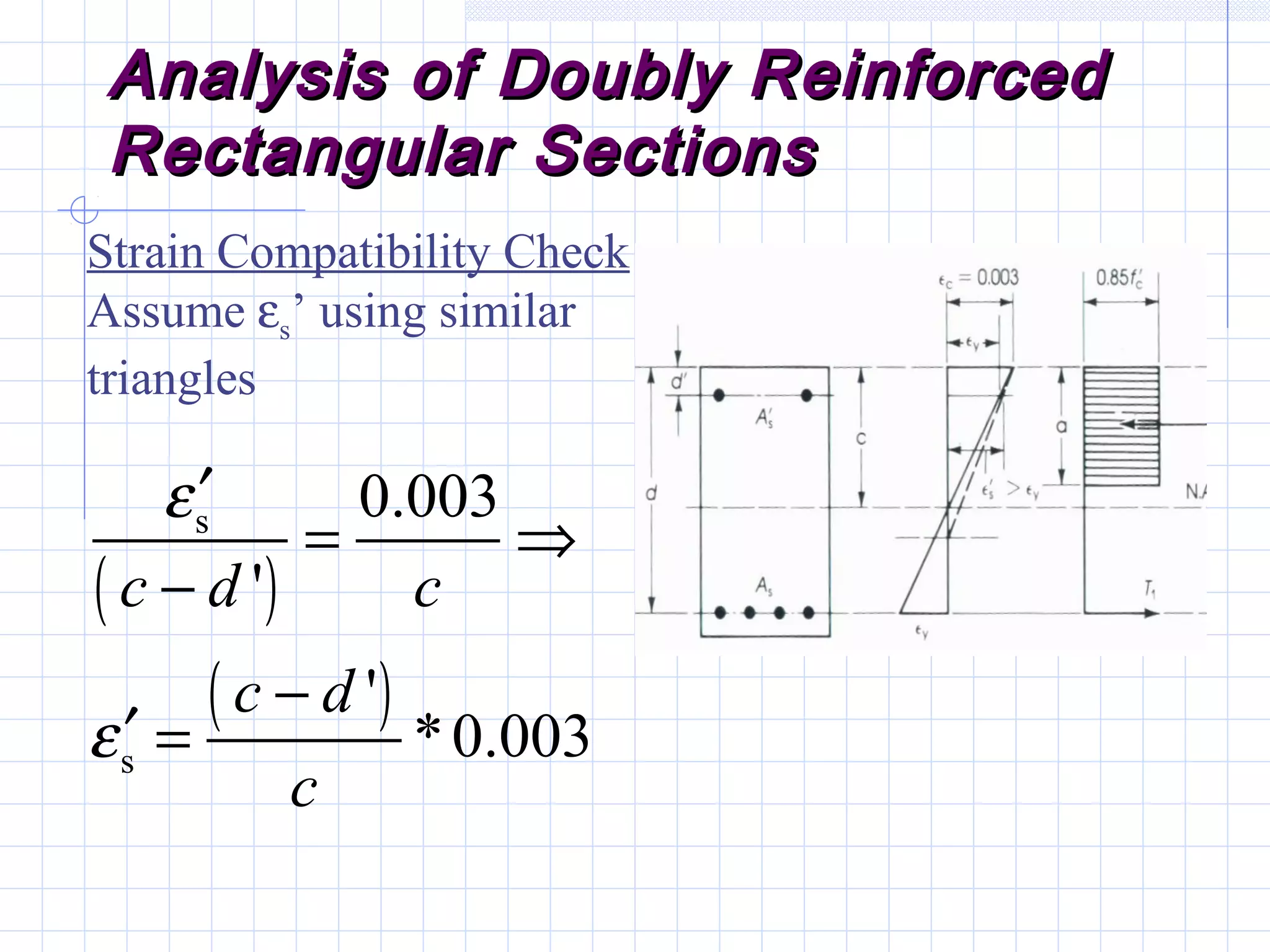
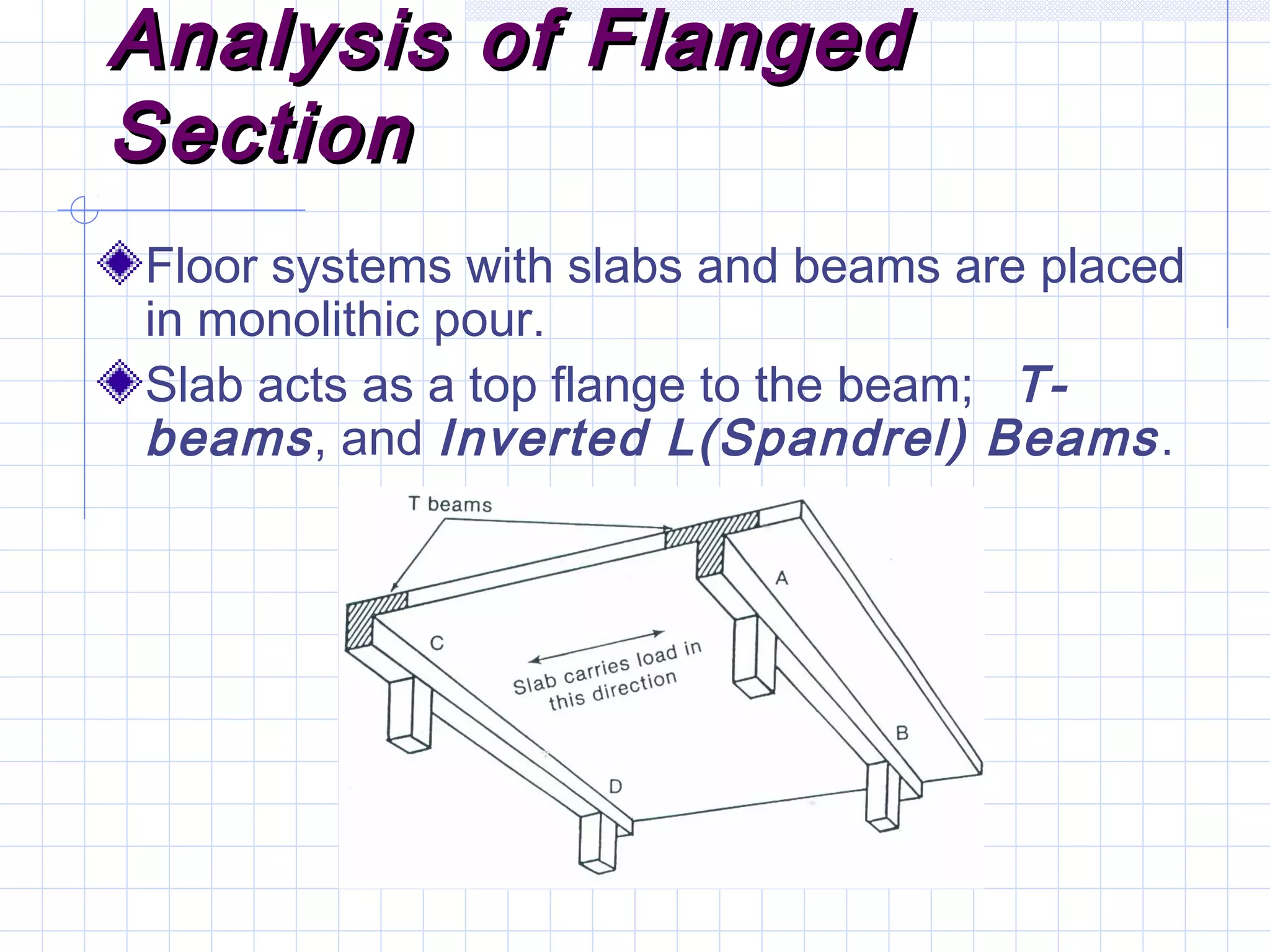
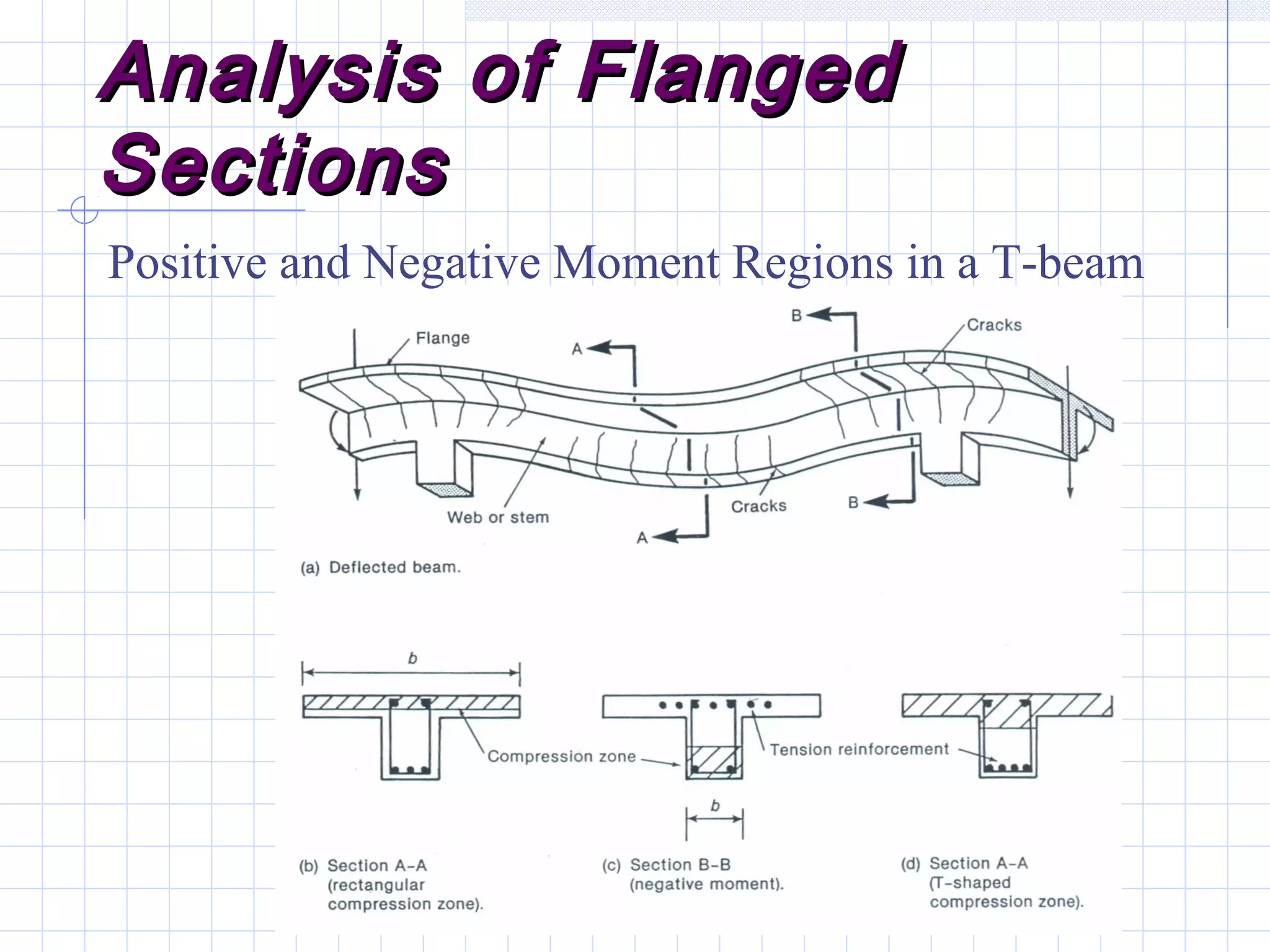
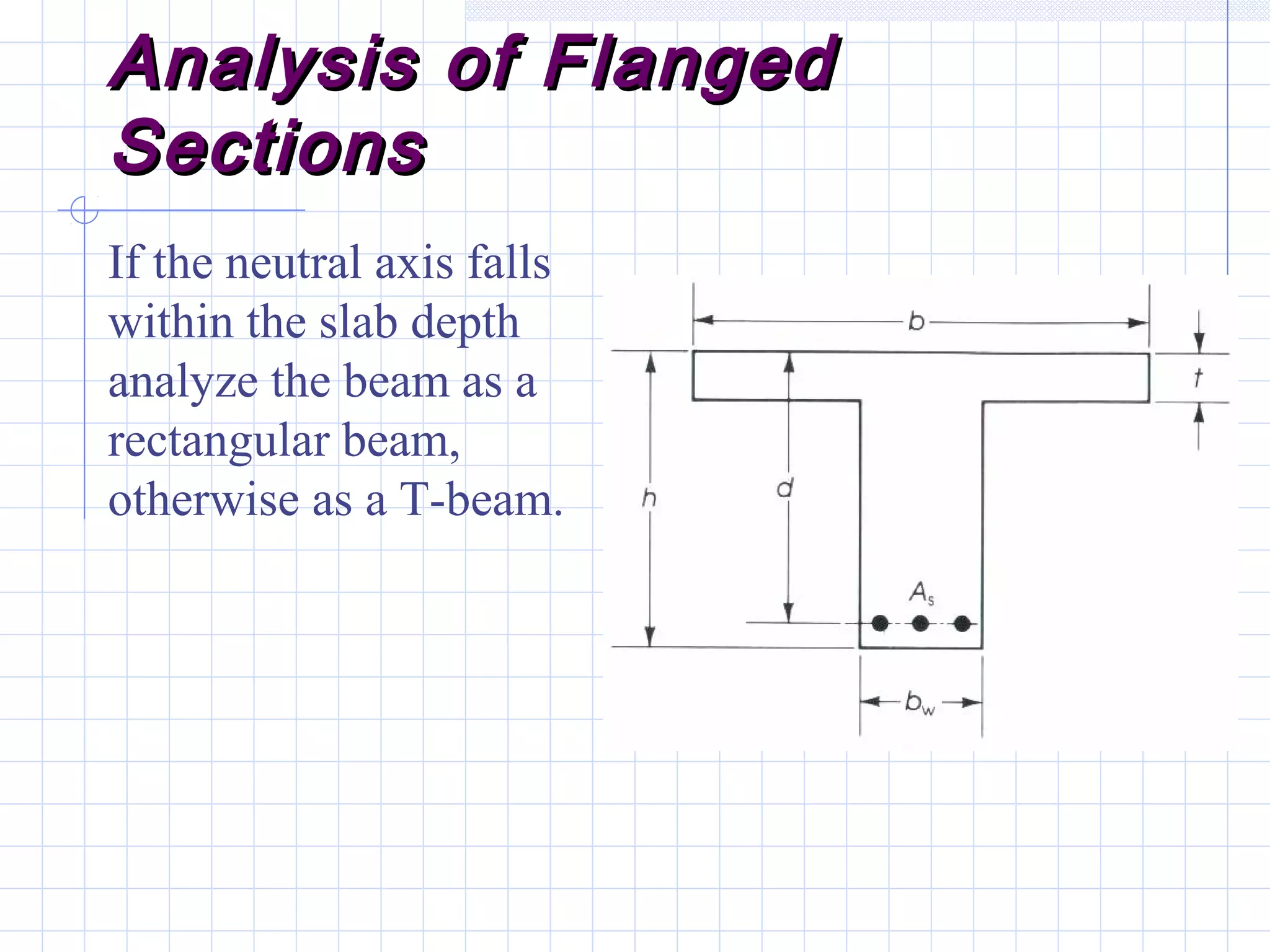
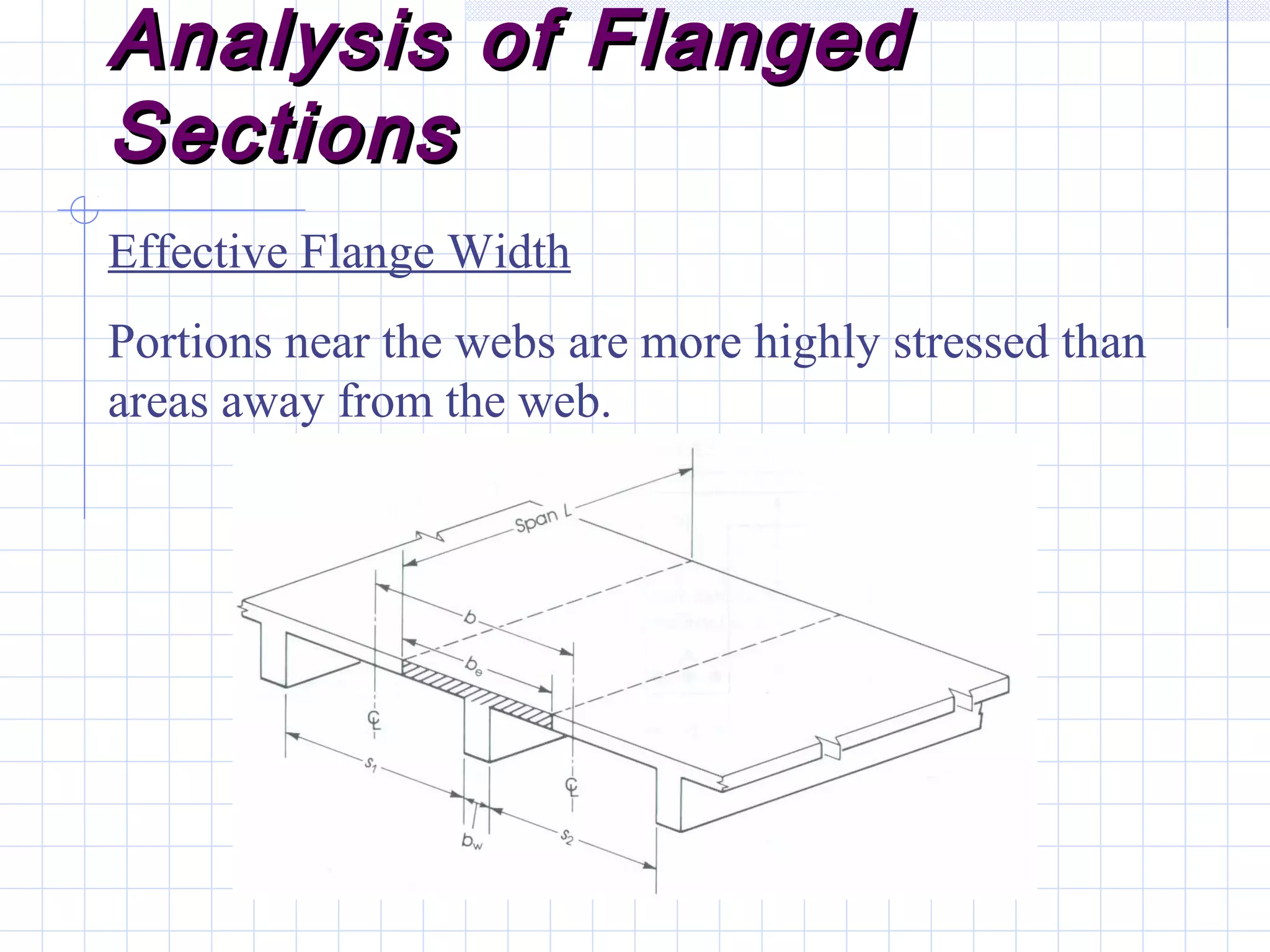
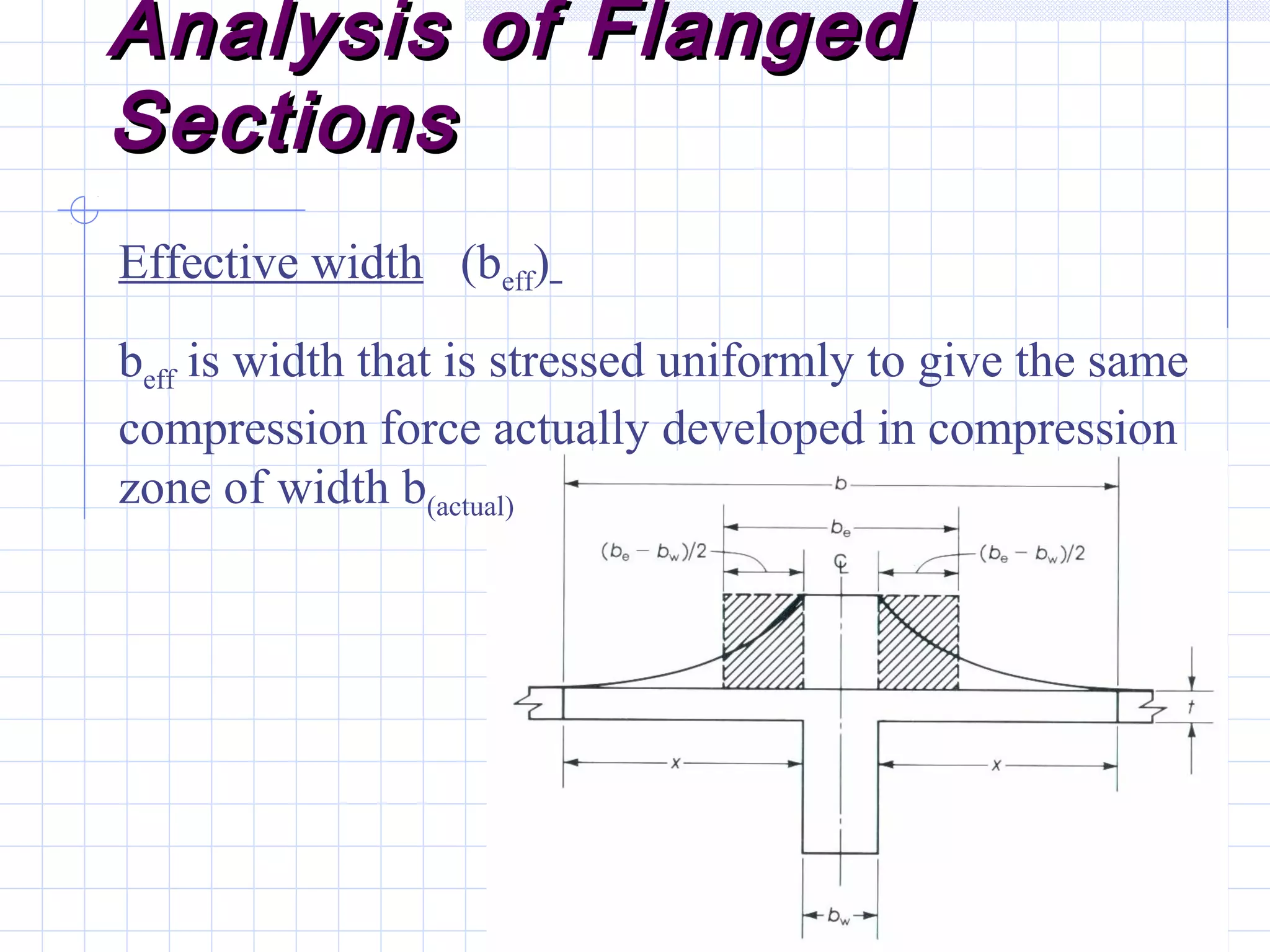
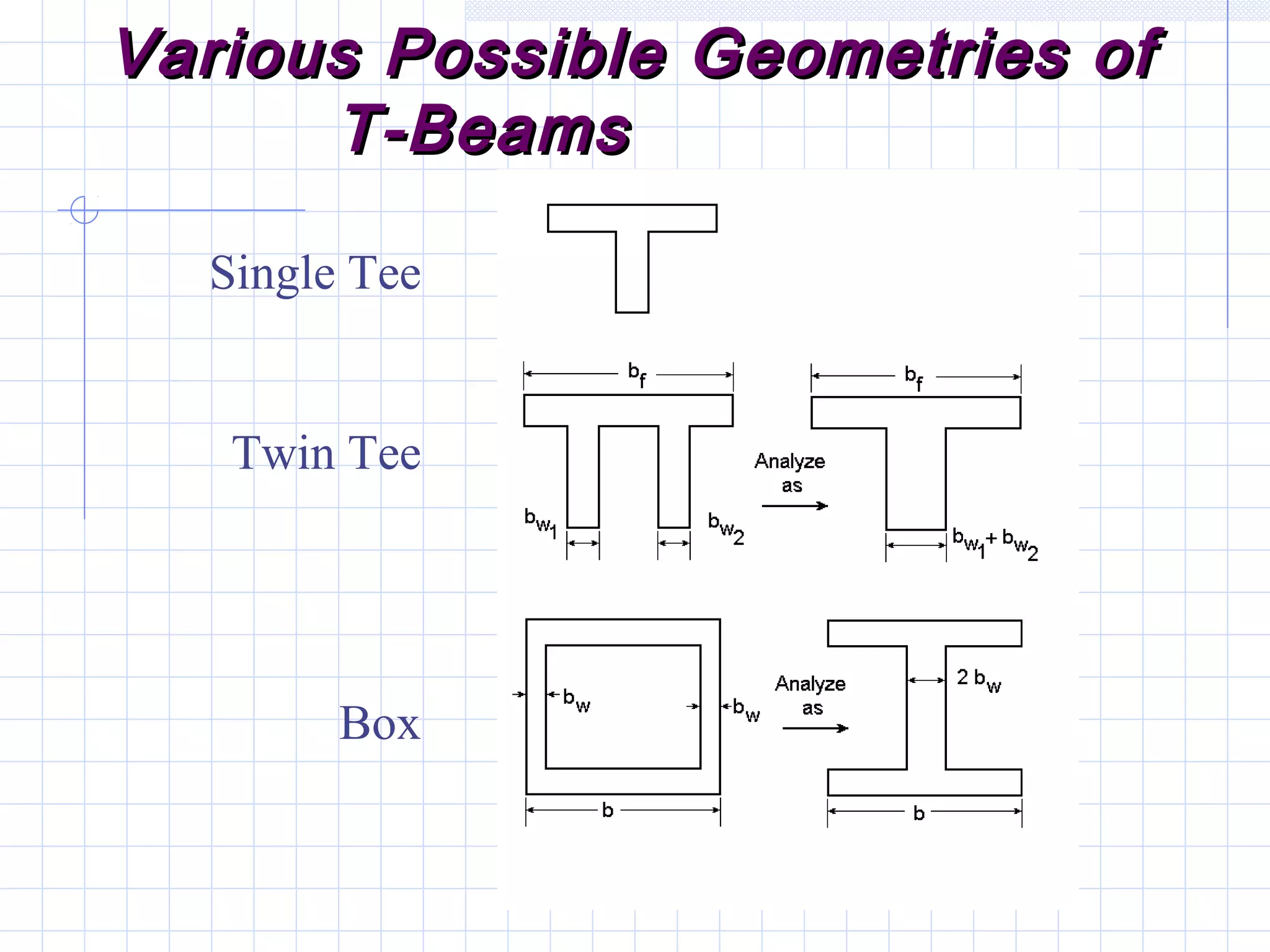
The document discusses analysis of doubly reinforced concrete beams. It begins by explaining how compression reinforcement allows less concrete to resist tension, moving the neutral axis up. It then provides the equations for analyzing strain compatibility and equilibrium in doubly reinforced sections. The document discusses finding the compression reinforcement strain and stress through iteration. It provides reasons for using compression reinforcement, including reducing deflection and increasing ductility. Finally, it includes an example problem demonstrating the full analysis process.