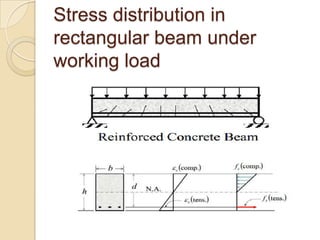
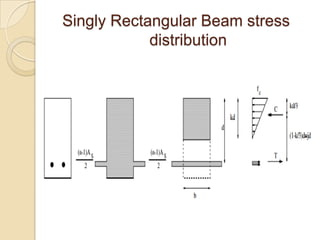
This document discusses the design of rectangular beams. It describes singly reinforced beams which have steel reinforcement only in the tensile zone below the neutral axis. It also describes doubly reinforced beams which have steel reinforcement in both the tensile and compressive zones. The key steps in the design of rectangular beams using the working stress method are described, including determining the stress distribution, calculating moments, and sizing the reinforcement. Design considerations like clear cover and bar spacing are also outlined.

1. Ahsanullah University of
Science and Technology
 NAME:
RAIHAN MANNAN
 STUDENT ID : 10.01.03.101
 SEC : B

2. MY TOPIC NAME
RECTANGULAR BEAM
DESIGN


Singly Rectangular Beam
Doubly Rectangular Beam
Under Working-stress Design

3. Section of Rectangular Beam

4. Stress distribution in
rectangular beam under
working load

5. Singly Rectangular Beam

A Beam is any structural member
which resists load mainly by bending.
Therefore it is also called flexural
member. Beam may be singly
reinforced or doubly reinforced. When
steel is provided only in tensile zone
(i.e. below neutral axis) is called
singly reinforced beam.

6. Assumptions for
DesignofMembers by Working
Stress Method



Plane sections before bending remain
plane after bending.
Normally, concrete is not considered for
taking the tensile stresses except
otherwise specifically permitted.
Therefore, all tensile stresses are taken
up by reinforcement only.
The stress-strain relationship of steel
and concrete is a straight line under
working loads.

7. Singly Rectangular Beam stress
distribution

8. Where,
 Jd =momnet arm=(1-k/3)
 Compressive force ,
C =(bkd/2)fc
 Tensile force ,
T = Asfs

9. 
neutral axis is determined by equating the
moment of the tension area to the moment
of the compression area

10. Moment calculation:

Start by determining

11. Reinforcement calculation:

12. Design equation for singly reinforcement
beam

13. Doubly Reinforcement
beam

If a beam cross section is limited
because of architectural or other
considerations, it may happen that the
concrete can not develop the
compression force required to resist
the given bending moment, in this
case ,reinforcement is added in the
compression zone, resulting in so
called Doubly reinforced beam
.i.e., one with compression as well as
tension reinforcement.

14. Why Doubly reinforcement
used
If concrete can not develop the
required compressive force to resist
the maximum bending moment, then
additional reinforcement is provide in
the compression zone.
 Reinforcement is provided in both
compression and tension zone.


15. Stress distribution in doubly
reinforced beam

16. Development of moment

In stress distibution,the design
moment is more than the balanced
moment of resistance of the section,
M = M1 + M2
The additional moment M2 is resisted
by providing compression
reinforcement As’
and additional tensile reinforcement
As2

17. Moment calculation

Moment is obtained by,
M1=(fc/2)kjbd^2
= As1fsjd
M2=As2fs(d-d’)
=As’fs’(d-d’)

18. Reinforcement in Beam
The total tensile reinforcement Ast
has two components As1+As2 for M1
and M2
 The equation of Ast,

Ast=As1+As2
Where, As1=
(bd/100)
And
As2 = M2/[Ó (d-d’)]
 compressive
reinforcement,

19. Clear cover for design
Not less than 1.5 in. when there is
no exposure to weather or contact
with the ground
 For exposure to aggressive weather
2 in.


20. CLEAR DISTENCE OF
REINFORCEMENT

Clear distance between parallel
bars in a layer must not be less
than the bar diameter or 1 in.

21. IF YOU
HAVE ANY
QUESTION THEN
YOU CAN ASK ME