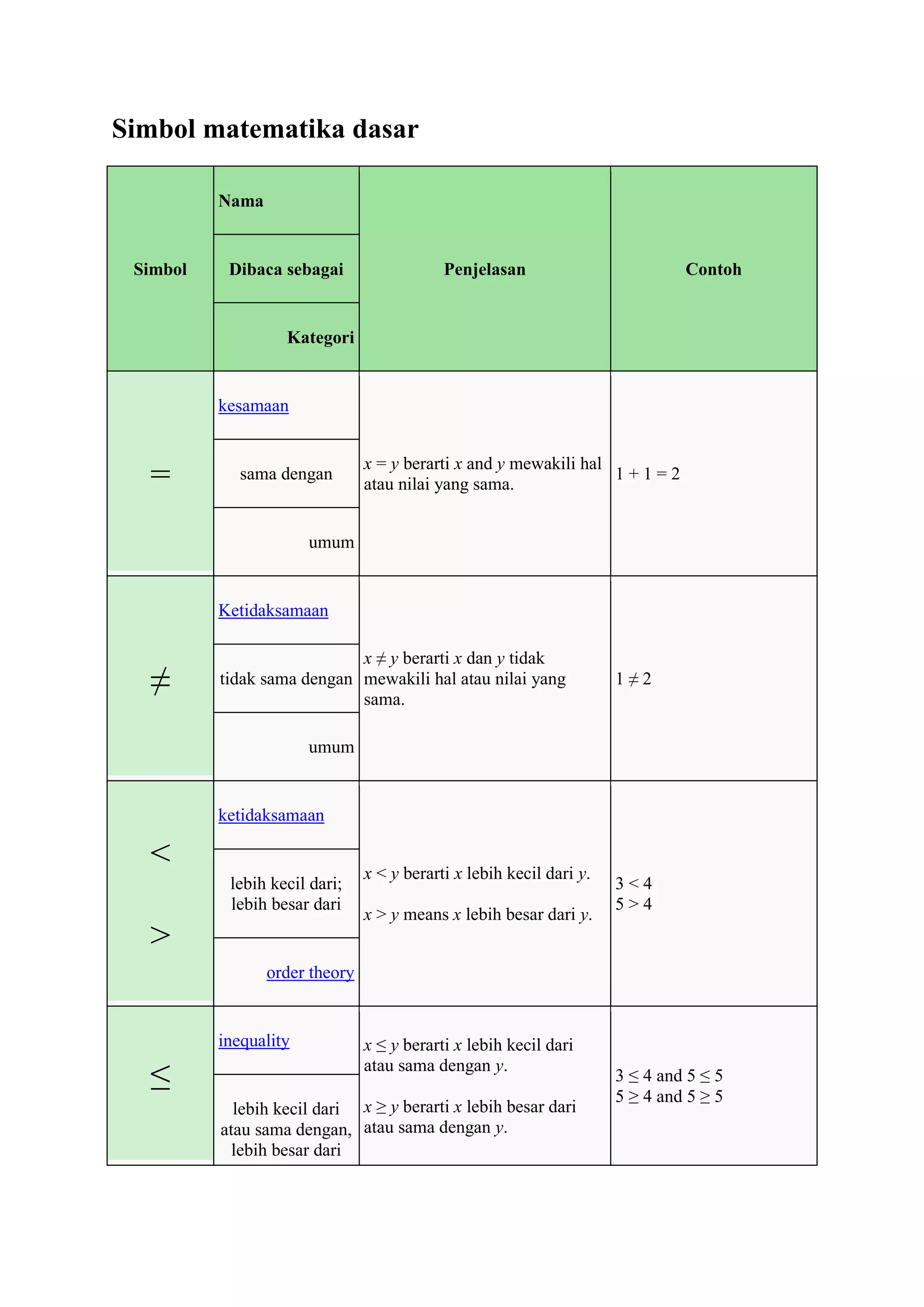
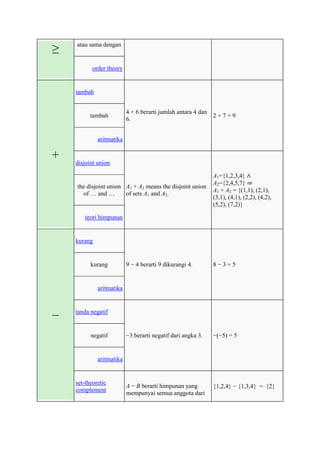
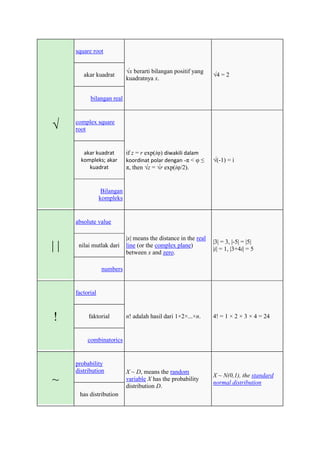
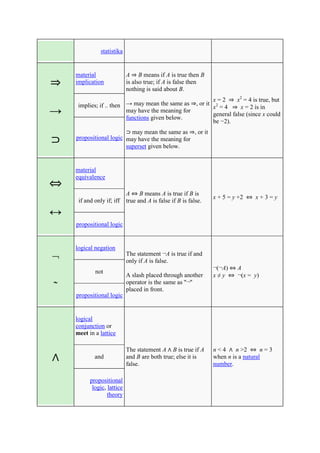
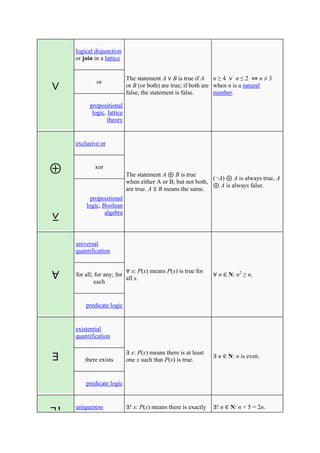
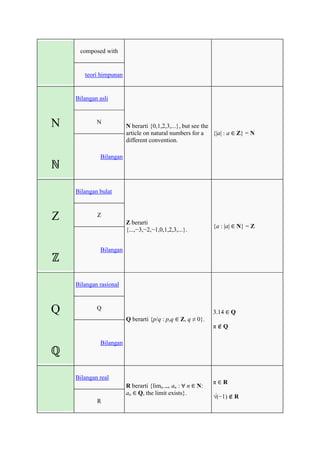
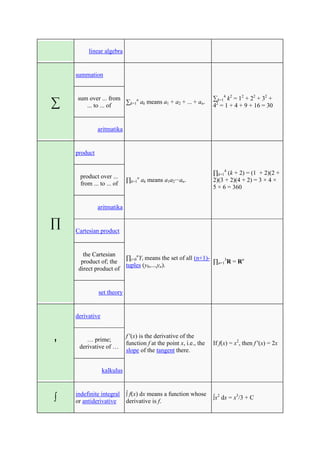
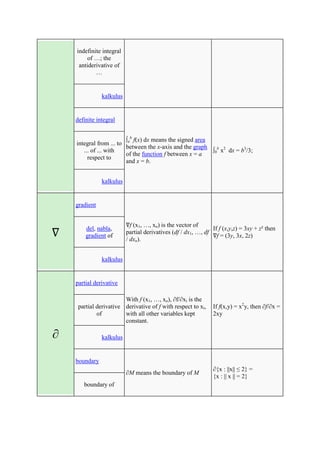
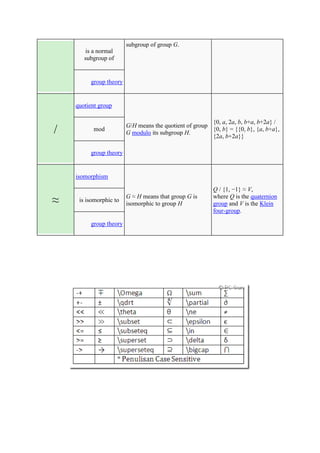
The document defines and provides examples of common mathematical symbols. Some key symbols and their meanings include: = means equal to; ≠ means not equal to; < and > mean less than and greater than, respectively; + means addition; - means subtraction; × means multiplication; ÷ and / mean division. Other symbols covered include exponents, fractions, sets, logic, functions, and limits.

1. Simbol matematika dasar
Nama
Simbol Dibaca sebagai Penjelasan Contoh
Kategori
kesamaan
x = y berarti x and y mewakili hal
= sama dengan
atau nilai yang sama.
1+1=2
umum
Ketidaksamaan
x ≠ y berarti x dan y tidak
≠ tidak sama dengan mewakili hal atau nilai yang
sama.
1≠2
umum
ketidaksamaan
< x < y berarti x lebih kecil dari y.
lebih kecil dari; 3<4
lebih besar dari 5>4
x > y means x lebih besar dari y.
>
order theory
inequality x ≤ y berarti x lebih kecil dari
≤ atau sama dengan y.
3 ≤ 4 and 5 ≤ 5
5 ≥ 4 and 5 ≥ 5
lebih kecil dari x ≥ y berarti x lebih besar dari
atau sama dengan, atau sama dengan y.
lebih besar dari

2. ≥ atau sama dengan
order theory
tambah
4 + 6 berarti jumlah antara 4 dan
tambah 2+7=9
6.
aritmatika
+ disjoint union
A1={1,2,3,4} ∧
A2={2,4,5,7} ⇒
the disjoint union A1 + A2 means the disjoint union
A1 + A2 = {(1,1), (2,1),
of … and … of sets A1 and A2.
(3,1), (4,1), (2,2), (4,2),
(5,2), (7,2)}
teori himpunan
kurang
kurang 9 − 4 berarti 9 dikurangi 4. 8−3=5
aritmatika
− tanda negatif
negatif −3 berarti negatif dari angka 3. −(−5) = 5
aritmatika
set-theoretic
A − B berarti himpunan yang {1,2,4} − {1,3,4} = {2}
complement
mempunyai semua anggota dari

3. A yang tidak terdapat pada B.
minus; without
set theory
multiplication
kali 3 × 4 berarti perkalian 3 oleh 4. 7 × 8 = 56
aritmatika
Cartesian product
produk Cartesian
... dan ...; produk X × Y berarti himpunan semua
langsung dari ... pasangan memerintahkan dengan {1,2} × {3,4} =
× dan ... elemen pertama dari masing-
{(1,3),(1,4),(2,3),(2,4)}
masing pasangan dipilih dari X dan
elemen kedua yang dipilih dari Y.
teori himpunan
cross product
u × v means the cross product of (1,2,5) × (3,4,−1) =
cross
vectors u and v (−22, 16, − 2)
vector algebra
division
÷ 2 ÷ 4 = .5
bagi 6 ÷ 3 atau 6/3 berati 6 dibagi 3.
12/4 = 3
/
aritmatika

4. square root
√x berarti bilangan positif yang
akar kuadrat √4 = 2
kuadratnya x.
bilangan real
√ complex square
root
akar kuadrat if z = r exp(iφ) diwakili dalam
kompleks; akar koordinat polar dengan -π < φ ≤ √(-1) = i
kuadrat π, then √z = √r exp(iφ/2).
Bilangan
kompleks
absolute value
|x| means the distance in the real
|3| = 3, |-5| = |5|
|| nilai mutlak dari line (or the complex plane)
between x and zero.
|i| = 1, |3+4i| = 5
numbers
factorial
! faktorial n! adalah hasil dari 1×2×...×n. 4! = 1 × 2 × 3 × 4 = 24
combinatorics
probability
distribution X ~ D, means the random
X ~ N(0,1), the standard
~ variable X has the probability
distribution D.
normal distribution
has distribution

5. statistika
material A ⇒ B means if A is true then B
⇒ implication is also true; if A is false then
nothing is said about B.
x = 2 ⇒ x2 = 4 is true, but
→ may mean the same as ⇒, or it 2
implies; if .. then x = 4 ⇒ x = 2 is in
→ may have the meaning for
functions given below.
general false (since x could
be −2).
⊃ may mean the same as ⇒, or it
⊃ propositional logic may have the meaning for
superset given below.
material
equivalence
⇔
A ⇔ B means A is true if B is
x + 5 = y +2 ⇔ x + 3 = y
if and only if; iff true and A is false if B is false.
↔
propositional logic
logical negation
The statement ¬A is true if and
¬ only if A is false.
¬(¬A) ⇔ A
not
A slash placed through another x ≠ y ⇔ ¬(x = y)
˜ operator is the same as "¬"
placed in front.
propositional logic
logical
conjunction or
meet in a lattice
The statement A ∧ B is true if A n < 4 ∧ n >2 ⇔ n = 3
∧ and and B are both true; else it is
false.
when n is a natural
number.
propositional
logic, lattice
theory

6. logical disjunction
or join in a lattice
The statement A ∨ B is true if A n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3
∨ or
or B (or both) are true; if both are when n is a natural
false, the statement is false. number.
propositional
logic, lattice
theory
exclusive or
⊕ xor
The statement A ⊕ B is true
(¬A) ⊕ A is always true, A
when either A or B, but not both,
⊕ A is always false.
are true. A ⊻ B means the same.
propositional
logic, Boolean
⊻
algebra
universal
quantification
∀ for all; for any; for
each
∀ x: P(x) means P(x) is true for
all x.
∀ n ∈ N: n2 ≥ n.
predicate logic
existential
quantification
∃ there exists
∃ x: P(x) means there is at least
one x such that P(x) is true.
∃ n ∈ N: n is even.
predicate logic
∃! x: P(x) means there is exactly ∃! n ∈ N: n + 5 = 2n.
∃! uniqueness

7. quantification one x such that P(x) is true.
there exists
exactly one
predicate logic
definition
:= x := y or x ≡ y means x is defined
to be another name for y (but cosh x := (1/2)(exp x +
is defined as note that ≡ can also mean other exp (−x))
≡ things, such as congruence).
A XOR B :⇔
P :⇔ Q means P is defined to be (A ∨ B) ∧ ¬(A ∧ B)
everywhere logically equivalent to Q.
:⇔
set brackets
{a,b,c} means the set consisting
{,} the set of ...
of a, b, and c.
N = {0,1,2,...}
teori himpunan
set builder
notation
{:} {x : P(x)} means the set of all x
{n ∈ N : n2 < 20} =
the set of ... such for which P(x) is true. {x | P(x)}
{0,1,2,3,4}
that ... is the same as {x : P(x)}.
{|}
teori himpunan
himpunan kosong
∅ berarti himpunan yang tidak
memiliki elemen. {} juga berarti {n ∈ N : 1 < n2 < 4} = ∅
hal yang sama.
∅ himpunan kosong

8. teori himpunan
{}
set membership
∈ is an element of; is a ∈ S means a is an element of (1/2)−1 ∈ N
not an element of the set S; a ∉ S means a is not an
element of S. 2−1 ∉ N
∉
everywhere, teori
himpunan
subset
⊆ A ⊆ B means every element of A
is also element of B.
is a subset of A ∩ B ⊆ A; Q ⊂ R
A ⊂ B means A ⊆ B but A ≠ B.
⊂
teori himpunan
superset
⊇ A ⊇ B means every element of B
is also element of A.
is a superset of A ∪ B ⊇ B; R ⊃ Q
A ⊃ B means A ⊇ B but A ≠ B.
⊃
teori himpunan
set-theoretic union
A ∪ B means the set that contains
∪ the union of ... and
...; union
all the elements from A and also A ⊆ B ⇔ A ∪ B = B
all those from B, but no others.
teori himpunan
∩ set-theoretic
intersection
A ∩ B means the set that contains {x ∈ R : x2 = 1} ∩ N = {1}
all those elements that A and B

9. have in common.
intersected with;
intersect
teori himpunan
set-theoretic
complement
A B means the set that contains
{1,2,3,4} {3,4,5,6} =
minus; without
all those elements of A that are
not in B.
{1,2}
teori himpunan
function
application
f(x) berarti nilai fungsi f pada Jika f(x) := x2, maka f(3) =
of elemen x. 32 = 9.
() teori himpunan
precedence
grouping
Perform the operations inside the (8/4)/2 = 2/2 = 1, but
parentheses first. 8/(4/2) = 8/2 = 4.
umum
function arrow
f: X → Y means the function f Let f: Z → N be defined by
f:X→Y from ... to
maps the set X into the set Y. f(x) = x2.
teori himpunan
function fog is the function, such that if f(x) = 2x, and g(x) = x +
o composition (fog)(x) = f(g(x)). 3, then (fog)(x) = 2(x + 3).

10. composed with
teori himpunan
Bilangan asli
N N
N berarti {0,1,2,3,...}, but see the
article on natural numbers for a {|a| : a ∈ Z} = N
different convention.
Bilangan
ℕ
Bilangan bulat
Z Z
Z berarti
{a : |a| ∈ N} = Z
{...,−3,−2,−1,0,1,2,3,...}.
Bilangan
ℤ
Bilangan rasional
Q Q
3.14 ∈ Q
Q berarti {p/q : p,q ∈ Z, q ≠ 0}.
π∉Q
Bilangan
ℚ
Bilangan real
π∈R
R berarti {limn→∞ an : ∀ n ∈ N:
an ∈ Q, the limit exists}.
√(−1) ∉ R
R

11. R
Bilangan
ℝ
Bilangan
kompleks
C C
C means {a + bi : a,b ∈ R}. i = √(−1) ∈ C
ℂ Bilangan
infinity
∞ is an element of the extended
∞ infinity
number line that is greater than
all real numbers; it often occurs
limx→0 1/|x| = ∞
in limits.
numbers
pi
π berarti perbandingan (rasio) A = πr² adalah luas
π pi
antara keliling lingkaran dengan
diameternya.
lingkaran dengan jari-jari
(radius) r
Euclidean
geometry
norm
||x|| is the norm of the element x
|| || of a normed vector space.
||x+y|| ≤ ||x|| + ||y||
norm of; length of

12. linear algebra
summation
∑k=14 k2 = 12 + 22 + 32 +
∑ sum over ... from
... to ... of
∑k=1n ak means a1 + a2 + ... + an.
42 = 1 + 4 + 9 + 16 = 30
aritmatika
product
∏k=14 (k + 2) = (1 + 2)(2 +
product over ...
∏k=1n ak means a1a2···an. 2)(3 + 2)(4 + 2) = 3 × 4 ×
from ... to ... of
5 × 6 = 360
aritmatika
∏ Cartesian product
the Cartesian
∏i=0nYi means the set of all (n+1)-
product of; the ∏n=13R = Rn
tuples (y0,...,yn).
direct product of
set theory
derivative
f '(x) is the derivative of the
… prime;
' derivative of …
function f at the point x, i.e., the
slope of the tangent there.
If f(x) = x2, then f '(x) = 2x
kalkulus
indefinite integral ∫ f(x) dx means a function whose
∫ or antiderivative derivative is f.
∫x2 dx = x3/3 + C

13. indefinite integral
of …; the
antiderivative of
…
kalkulus
definite integral
∫ b f(x) dx means the signed area
integral from ... to a
between the x-axis and the graph
... of ... with ∫0b x2 dx = b3/3;
of the function f between x = a
respect to
and x = b.
kalkulus
gradient
∇f (x1, …, xn) is the vector of
∇ del, nabla,
gradient of
partial derivatives (df / dx1, …, df
/ dxn).
If f (x,y,z) = 3xy + z² then
∇f = (3y, 3x, 2z)
kalkulus
partial derivative
With f (x1, …, xn), ∂f/∂xi is the
partial derivative derivative of f with respect to xi, If f(x,y) = x2y, then ∂f/∂x =
of with all other variables kept 2xy
constant.
∂ kalkulus
boundary
∂{x : ||x|| ≤ 2} =
∂M means the boundary of M
{x : || x || = 2}
boundary of

14. topology
perpendicular
x ⊥ y means x is perpendicular to
is perpendicular to y; or more generally x is If l⊥m and m⊥n then l || n.
orthogonal to y.
geometri
⊥ bottom element
the bottom x = ⊥ means x is the smallest
∀x : x ∧ ⊥ = ⊥
element element.
lattice theory
entailment
A ⊧ B means the sentence A
entails the sentence B, that is
|= entails
every model in which A is true, B
A ⊧ A ∨ ¬A
is also true.
model theory
inference
infers or is derived
from
|- x ⊢ y means y is derived from x. A → B ⊢ ¬B → ¬A
propositional
logic, predicate
logic
normal subgroup Z(G) ◅ G
◅ N ◅ G means that N is a normal

15. subgroup of group G.
is a normal
subgroup of
group theory
quotient group
{0, a, 2a, b, b+a, b+2a} /
G/H means the quotient of group
/ mod
G modulo its subgroup H.
{0, b} = {{0, b}, {a, b+a},
{2a, b+2a}}
group theory
isomorphism
Q / {1, −1} ≈ V,
G ≈ H means that group G is
≈ is isomorphic to
isomorphic to group H
where Q is the quaternion
group and V is the Klein
four-group.
group theory