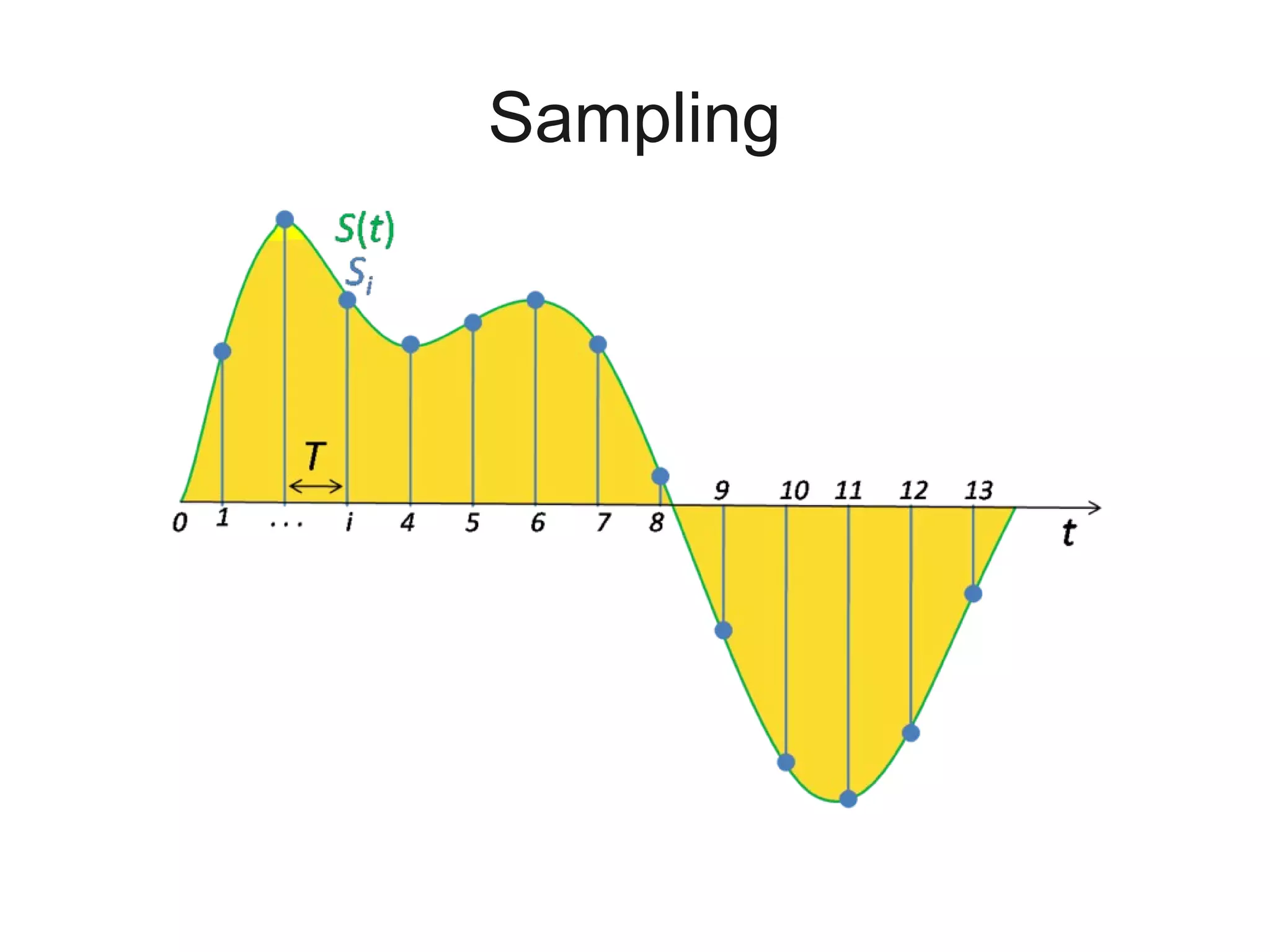
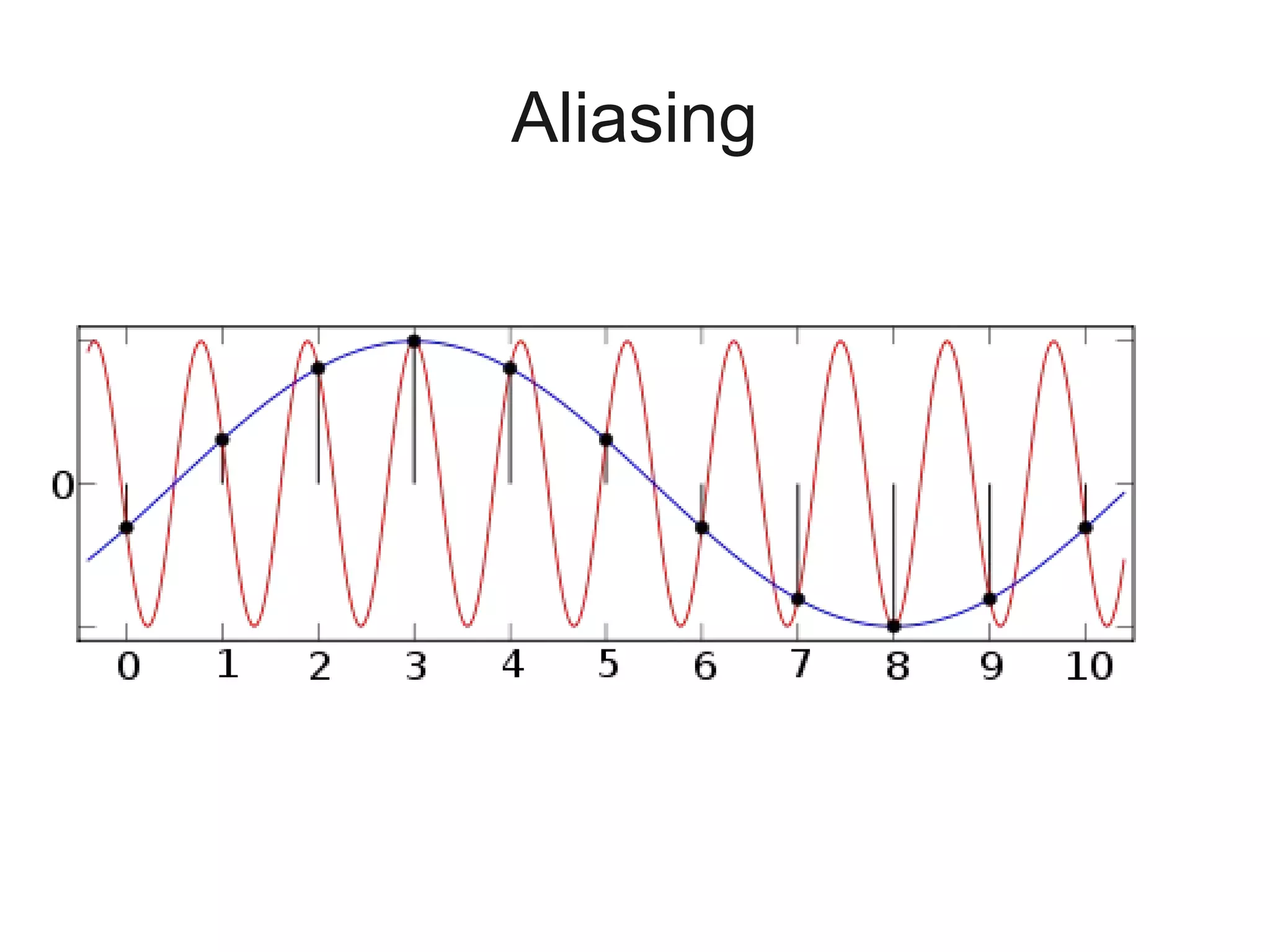
This document is a tutorial on digital signal processing using Python, focusing on audio analysis and manipulation. It covers concepts like Fourier transforms, signal visualization, sampling, and filtering, while providing hands-on coding exercises that encourage interactive learning. The tutorial is designed for participants with basic knowledge of Python and aims to accomplish in three hours what typically takes 144 hours in a standard class.

1. Digital Signal Processing through
Speech, Hearing, and Python
Mel Chua
PyCon 2013
This tutorial was designed to be run on a free
pythonanywhere.com Python 2.7 terminal.
If you want to run the code directly on your machine,
you'll need python 2.7.x, numpy, scipy, and
matplotlib.
Either way, you'll need a .wav file to play with
(preferably 1-2 seconds long).

2. Agenda
● Introduction
● Fourier transforms, spectrums, and spectrograms
● Playtime!
● SANITY BREAK
● Nyquist, sampling and aliasing
● Noise and filtering it
● (if time permits) formants, vocoding, shifting, etc.
● Recap: so, what did we do?

3. What's signal processing?
● Usually an upper-level undergraduate engineering
class
● Prerequisites: circuit theory, differential equations,
MATLAB programming, etc, etc...
● About 144 hours worth of work (3 hours per credit
per week, 3 credits, 16 weeks)
● We're going to do this in 3 hours (1/48th the time)
● I assume you know basic Python and therefore
algebra

4. Therefore
We'll skip a lot of stuff.

5. We will not...
● Do circuit theory, differential equations,
MATLAB programming, etc, etc...
● Work with images
● Write tons of code from scratch
● See rigorous proofs, math, and/or definitions

6. We will...
● Play with audio
● Visualize audio
● Generate and record audio
● In general, play with audio
● Do a lot of “group challenge time!”

7. Side notes
● This is based on a graduate class teaching
signal processing to audiology majors
● We've had half a semester to do everything
(about 70 hours)
● I'm not sure how far we will get today

8. Introduction: Trig In One Slide

9. Sampling

10. Let's write some code.
Open up the terminal and follow along.
We assume you have a file called 'flute.wav' in
the directory you are running the terminal from.

11. Import the libraries we need...
from numpy import *

12. ...and create some data.
Here we're making a signal
consisting of 2 sine waves
(1250Hz and 625Hz)
sampled at a 10kHz rate.
x = arange(256.0)
sin1 = sin(2*pi*(1250.0/10000.0)*x)
sin2 = sin(2*pi*(625.0/10000.0)*x)
sig = sin1 + sin2

13. What does this look like?
Let's plot it and find out.
import matplotlib.pyplot as pyplot
pyplot.plot(sig)
pyplot.savefig('sig.png')
pyplot.clf() # clear plot

14. sig.png

15. While we're at it, let's define a
graphing function so we don't need
to do this all again.
def makegraph(data, filename):
pyplot.clf()
pyplot.plot(data)
pyplot.savefig(filename)

16. Our first plot showed the signal in
the time domain. We want to see it
in the frequency domain.
A numpy function that implements
an algorithm called the Fast Fourier
Transform (FFT) can take us there.
data = fft.rfft(sig)
# note that we use rfft because
# the values of sig are real
makegraph(data, 'fft0.png')

17. fft0.png

18. That's a start.
We had 2 frequencies in the signal,
and we're seeing 2 spikes here, so
that seems reasonable.
But we did get this warning.
>>> makegraph(data, 'fft0.png')
/usr/local/lib/python2.7/site-
packages/numpy/core/numeric.py:320:
ComplexWarning:
Casting complex values to real discards the
imaginary part
return array(a, dtype, copy=False, order=order)

19. That's because the fourier transform
gave us a complex output – so we
need to take the magnitude of the
complex output...
data = abs(data)
makegraph(data, 'fft1.png')
# more detail: sigproc-outline.py
# lines 42-71

20. fft1.png

21. But this is displaying raw power
output, and we usually think of audio
volume in terms of decibels.
Wikipedia tells us decibels (dB) are
the original signal plotted on a
10*log10 y-axis, so...
data = 10*log10(data)
makegraph(data, 'fft2.png')

22. fft2.png

23. We see our 2 pure tones showing
up as 2 peaks – this is great. The
jaggedness of the rest of the signal
is quantization noise, a.k.a.
numerical error, because we're
doing this with approximations.
Question: what's the relationship of
the x-axis of the graph and the
frequency of the signal?

24. Answer: the numpy fft function goes
from 0-5000Hz by default.
This means the x-axis markers
correspond to values of 0-5000Hz
divided into 128 slices.
5000/128 = 39.0625 Hz per marker

25. The two peaks are at 16 and 32.
(5000/128)*16 = close to 625Hz
(5000/128)*32 = close to 1250Hz
...which are our 2 original tones.

26. Another visualization: spectrogram

27. Generate and plot a spectrogram...
from pylab import specgram
pyplot.clf()
sgram = specgram(sig)
pyplot.savefig('sgram.png')

28. sgram.png

29. Do you see how the spectrogram is
sort of like our last plot, extruded
forward out of the screen, and
looked down upon from above?
That's a spectrogram. Time is on the
x-axis, frequency on the y-axis,and
amplitude is marked by color.

30. Now let's do this with a more
complex sound. We'll need to use a
library to read/write .wav files.
import scipy
from scipy.io.wavfile import read

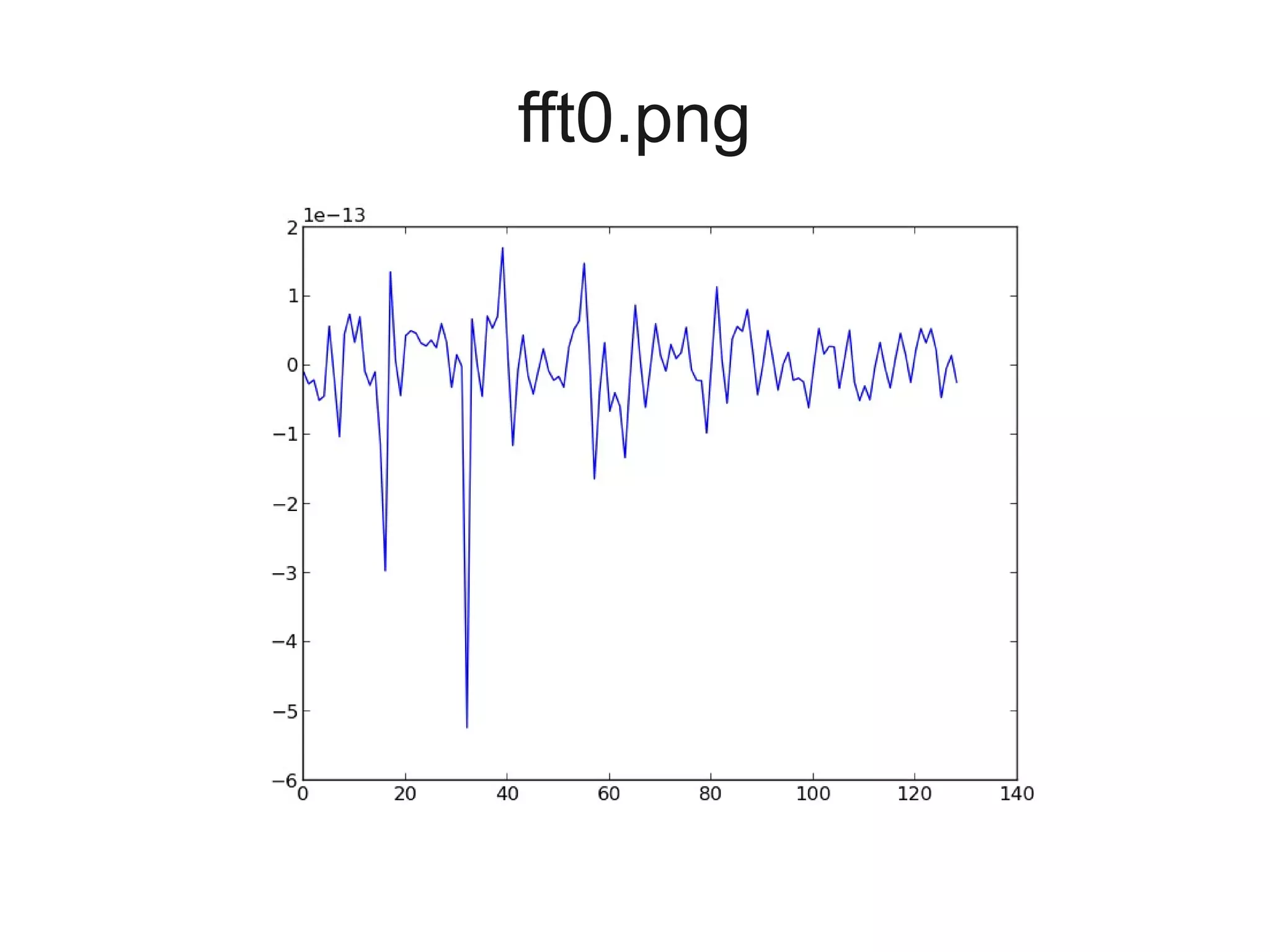
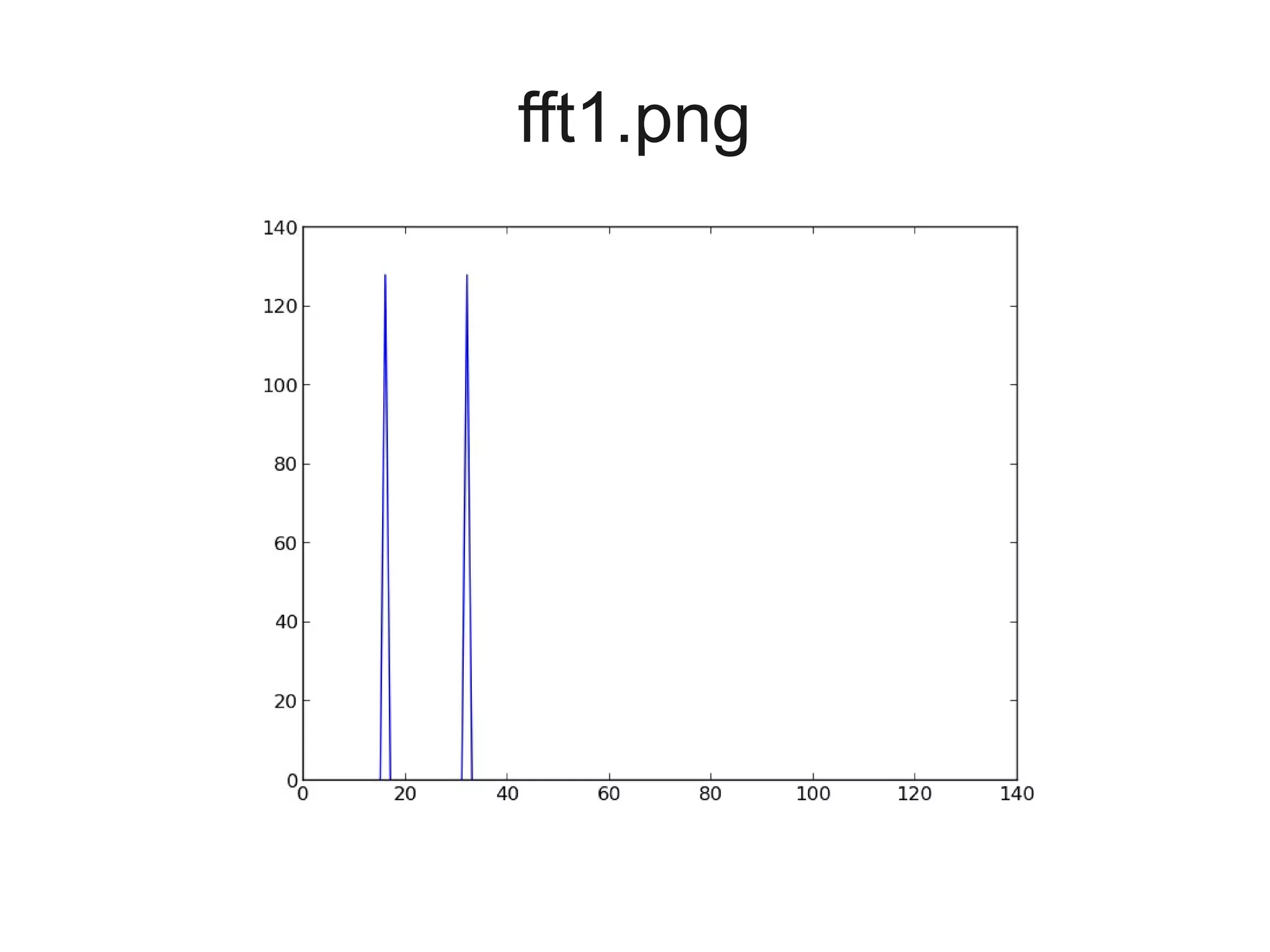
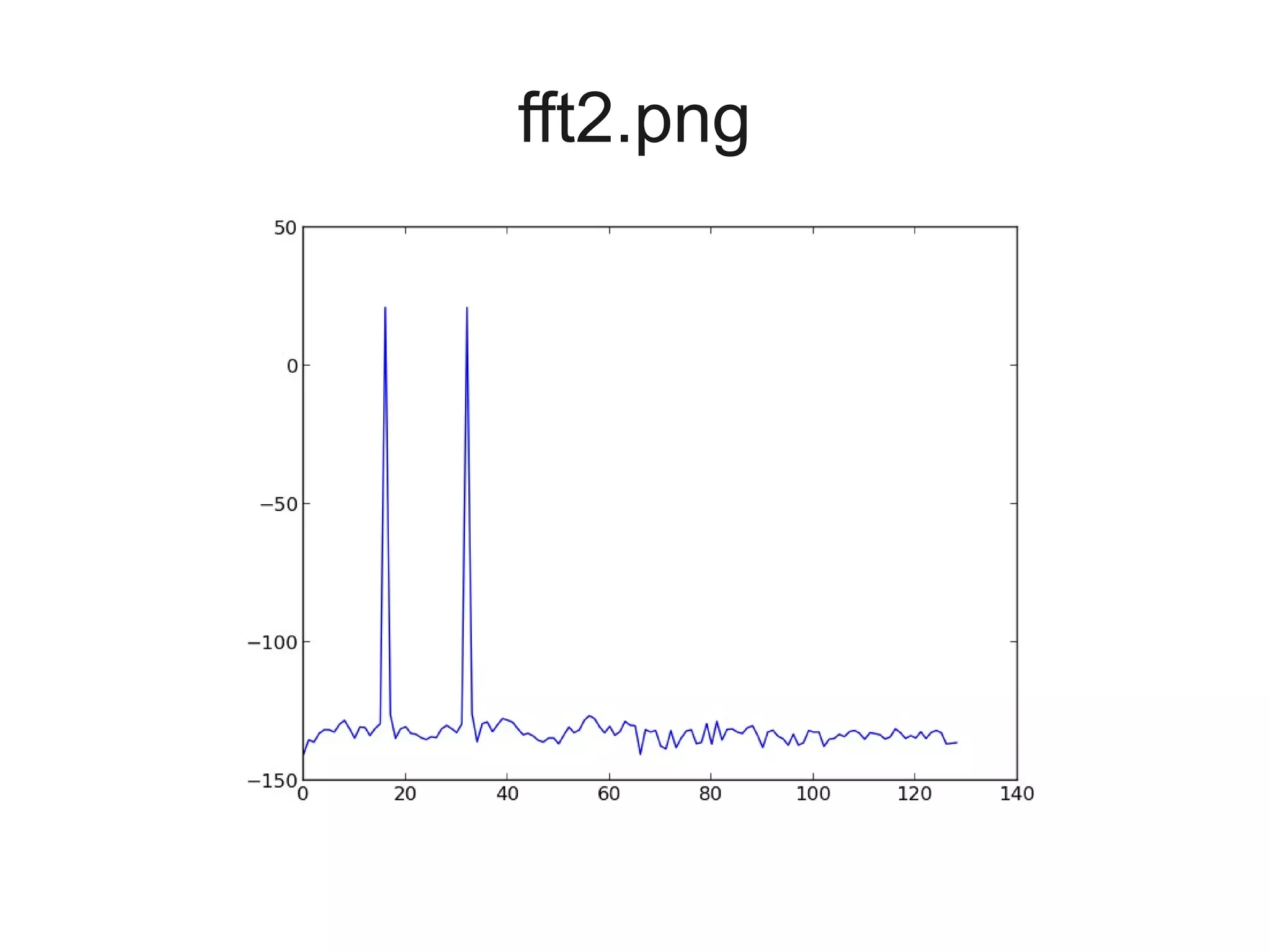
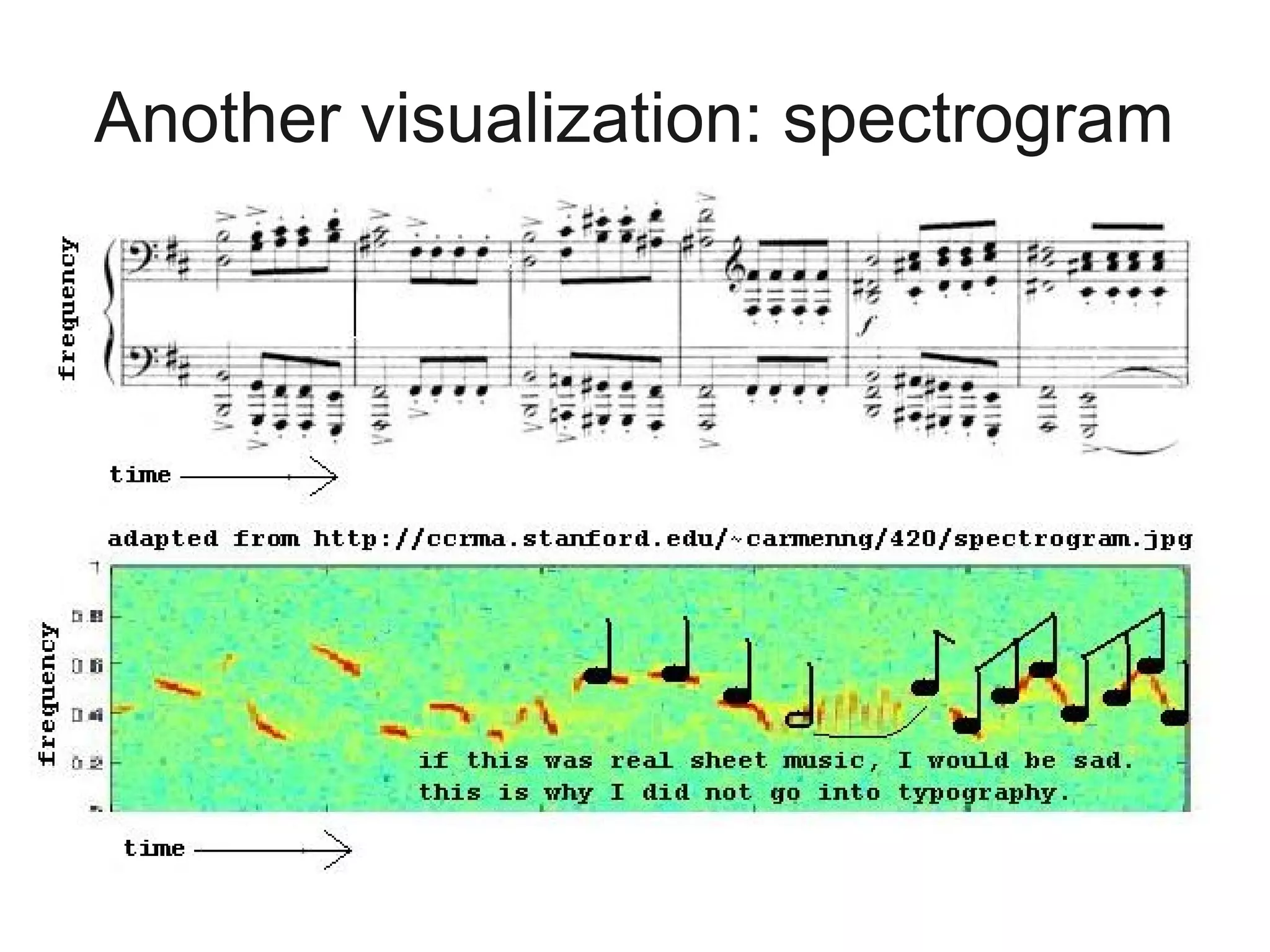
31. Let's define a function to get the
data from the .wav file, and use it.
def getwavdata(file):
return scipy.io.wavfile.read(file)[1]
audio = getwavdata('flute.wav')
# more detail on scipy.io.wavfile.read
# in sigproc-outline.py, lines 117-123

32. Hang on! How do we make sure
we've got the right data? We could
write it back to a .wav file and make
sure they sound the same.
from scipy.io.wavfile import write
def makewav(data, outfile, samplerate):
scipy.io.wavfile.write(outfile, samplerate, data)
makewav(audio, 'reflute.wav', 44100)
# 44100Hz is the default CD sampling rate, and
# what most .wav files will use.

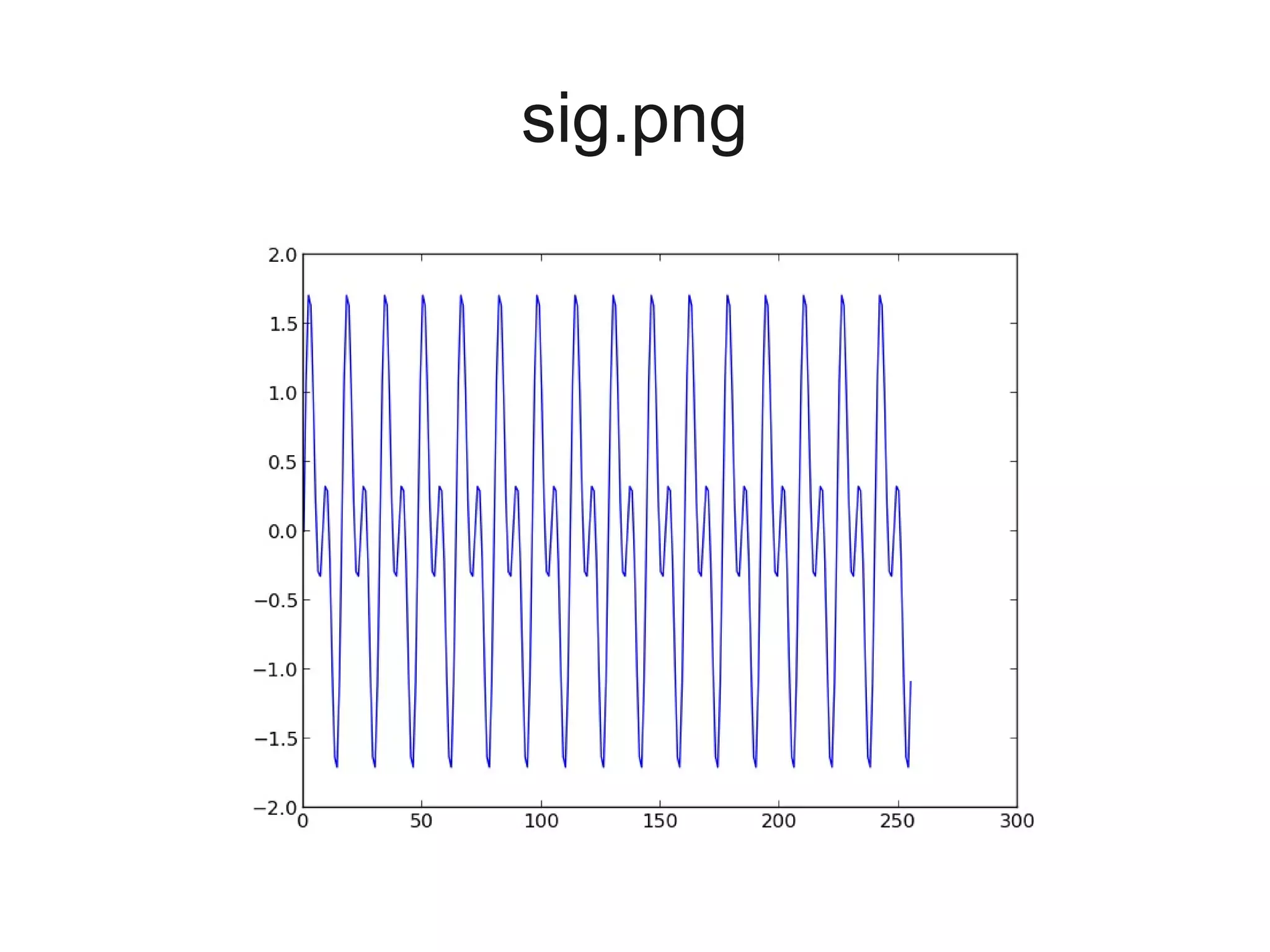
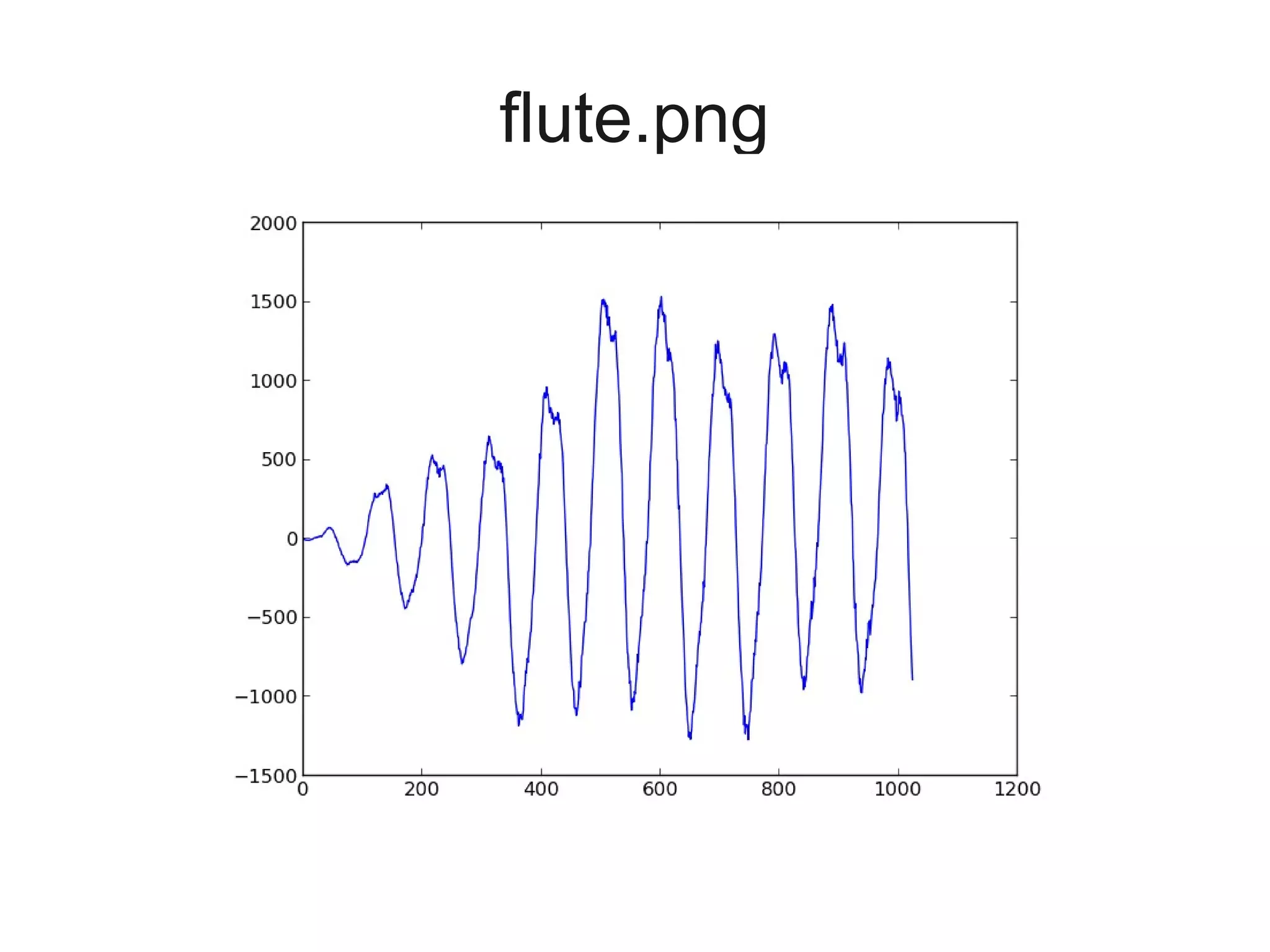
33. Now let's see what this looks like in
the time domain. We've got a lot of
data points, so we'll only plot the
beginning of the signal here.
makegraph(audio[0:1024], 'flute.png')

34. flute.png

35. What does this look like in the
frequency domain?
audiofft = fft.rfft(audio)
audiofft = abs(audiofft)
audiofft = 10*log10(audiofft)
makegraph(audiofft, 'flutefft.png')

36. flutefft.png

37. This is much more complex. We can
see harmonics on the left side.
Perhaps this will be clearer if we plot
it as a spectrogram.
pyplot.clf()
sgram = specgram(audio)
pyplot.savefig('flutespectro.png')

38. flutespectro.png

39. You can see the base note of the
flute (a 494Hz B) in dark red at the
bottom, and lighter red harmonics
above it.
http://www.bgfl.org/custom/resources_ftp/client_ftp/ks2/music/piano/flute.htm
http://en.wikipedia.org/wiki/Piano_key_frequencies

40. Your Turn: Challenge
● That first signal we made? Make a wav of it.
● Hint: you may need to generate more samples.
● Bonus: the flute played a B (494Hz) – generate
a single sinusoid of that.
● Megabonus: add the flute and sinusoid signals
and play them together

41. Your turn: Challenge 2
● Record some sounds on your computer
● Do an FFT on it
● Plot the spectrum
● Plot the spectrogram
● Bonus: add the flute and your sinusoid and plot their
spectrum and spectrogram together – what's the x scale?
● Bonus: what's the difference between fft/rfft?
● Bonus: numpy vs scipy fft libraries?
● Bonus: try the same sound at different frequencies (example:
vowels)

42. Sanity break?
Come back in 20 minutes, OR: stay for a demo
of the wave library (aka “why we're using scipy”)
note: wavlibraryexample.py contains the
wave library demo (which we didn't get to in the
actual workshop)

43. Things people found during break
Problem #1: When trying to generate a pure-tone
(sine wave) .wav file, the sound is not audible.
Underlying reason: The amplitude of a sine wave is
1, which is really, really tiny. Compare that to the
amplitude of the data you get when you read in the
flute.wav file – over 20,000.
Solution: Amplify your sine wave by multiplying it by
a large number (20,000 is good) before writing it to
the .wav file.

44. More things people found
Problem #2: The sine wave is audible in the
.wav file, but sounds like white noise rather
than a pure tone.
Underlying reason: scipy.io.wavfile.write()
expects an int16 datatype, and you may be
giving it a float instead.
Solution: Coerce your data to int16 (see next
slide).

45. Coercing to int16
# option 1: rewrite the makewav function
# so it includes type coercion
def savewav(data, outfile, samplerate):
out_data = array(data, dtype=int16)
scipy.io.wavfile.write(outfile, samplerate, out_data)
# option 2: generate the sine wave as int16
# which allows you to use the original makewav function
def makesinwav(freq, amplitude, sampling_freq,
num_samples):
return array(sin(2*pi*freq/float(sampling_freq)
*arange(float(num_samples)))*amplitude,dtype=int16)

46. Post-break: Agenda
● Introduction
● Fourier transforms, spectrums, and spectrograms
● Playtime!
● SANITY BREAK
● Nyquist, sampling and aliasing
● Noise and filtering it
● (if time permits) formants, vocoding, shifting, etc.
● Recap: so, what did we do?

47. Nyquist: sampling and aliasing
● The sample rate matters.
● Higher is better.
● There is a tradeoff.

48. Sampling

49. Aliasing

50. Nyquist-Shannon sampling theorem
(Shannon's version)
If a function x(t) contains no frequencies higher
than B hertz, it is completely determined by
giving its ordinates at a series of points spaced
1/(2B) seconds apart.

51. Nyquist-Shannon sampling theorem
(haiku version)
lowest sample rate
for sound with highest freq F
equals 2 times F

52. Let's explore the effects of sample
rate. When you listen to these .wav
files, note that doubling/halfing the
sample rate moves the sound
up/down an octave, respectively.
audio = getwavdata('flute.wav')
makewav(audio, 'fluteagain44100.wav', 44100)
makewav(audio, 'fluteagain22000.wav', 22000)
makewav(audio, 'fluteagain88200.wav', 88200)

53. Your turn
● Take some of your signals from earlier
● Try out different sample rates and see what
happens
● Hint: this is easier with simple sinusoids at first
● Hint: determine the highest frequency (your Nyquist
frequency), double it (that's your highest sampling
rate) and try sampling above, below, and at that
sampling frequency
● What do you find?

54. What do aliases alias at?
● They reflect around the sampling frequency
● Example: 40kHz sampling frequency
● Implies 20kHz Nyquist frequency
● So if we try to play a 23kHz frequency...
● ...it'll sound like 17kHz.
Your turn: make this happen with pure sinusoids
Bonus: with non-pure sinusoids

55. Agenda
● Introduction
● Fourier transforms, spectrums, and spectrograms
● Playtime!
● SANITY BREAK
● Nyquist, sampling and aliasing
● Noise and filtering it
● (if time permits) formants, vocoding, shifting, etc.
● Recap: so, what did we do?

56. Remember this?

57. Well, these are filters.

58. Noise and filtering it
● High pass
● Low pass
● Band pass
● Band stop
● Notch
● (there are many more, but these basics)

59. Notice that all these filters work in
the frequency domain.
We went from the time to the
frequency domain using an FFT.
# get audio (again) in the time domain
audio = getwavdata('flute.wav')
# convert to frequency domain
flutefft = fft.rfft(audio)

60. We can go back from the frequency
to the time domain using an inverse
FFT (IFFT).
reflute.wav should sound identical to
flute.wav.
reflute= fft.irfft(flutefft, len(audio))
reflute_coerced = array(reflute,
dtype=int16) # coerce to int16
makewav(reflute_coerced,
'fluteregenerated.wav', 44100)

61. Let's look at flute.wav in the
frequency domain again...
# plot on decibel (dB) scale
makegraph(10*log10(abs(flutefft)),
'flutefftdb.png')

62. What if we wanted to cut off all the
frequencies higher than the 5000th
index? (low-pass filter)

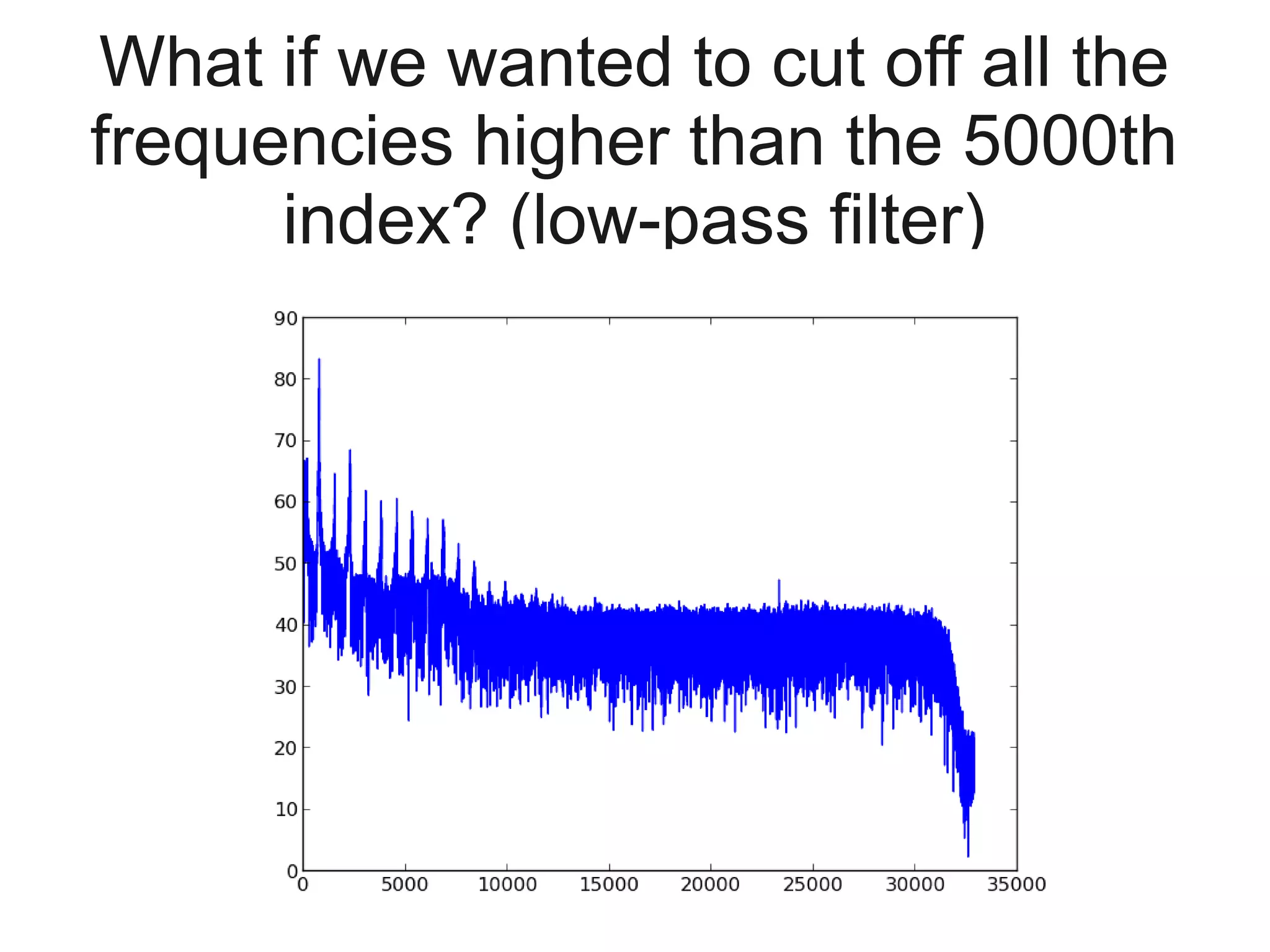
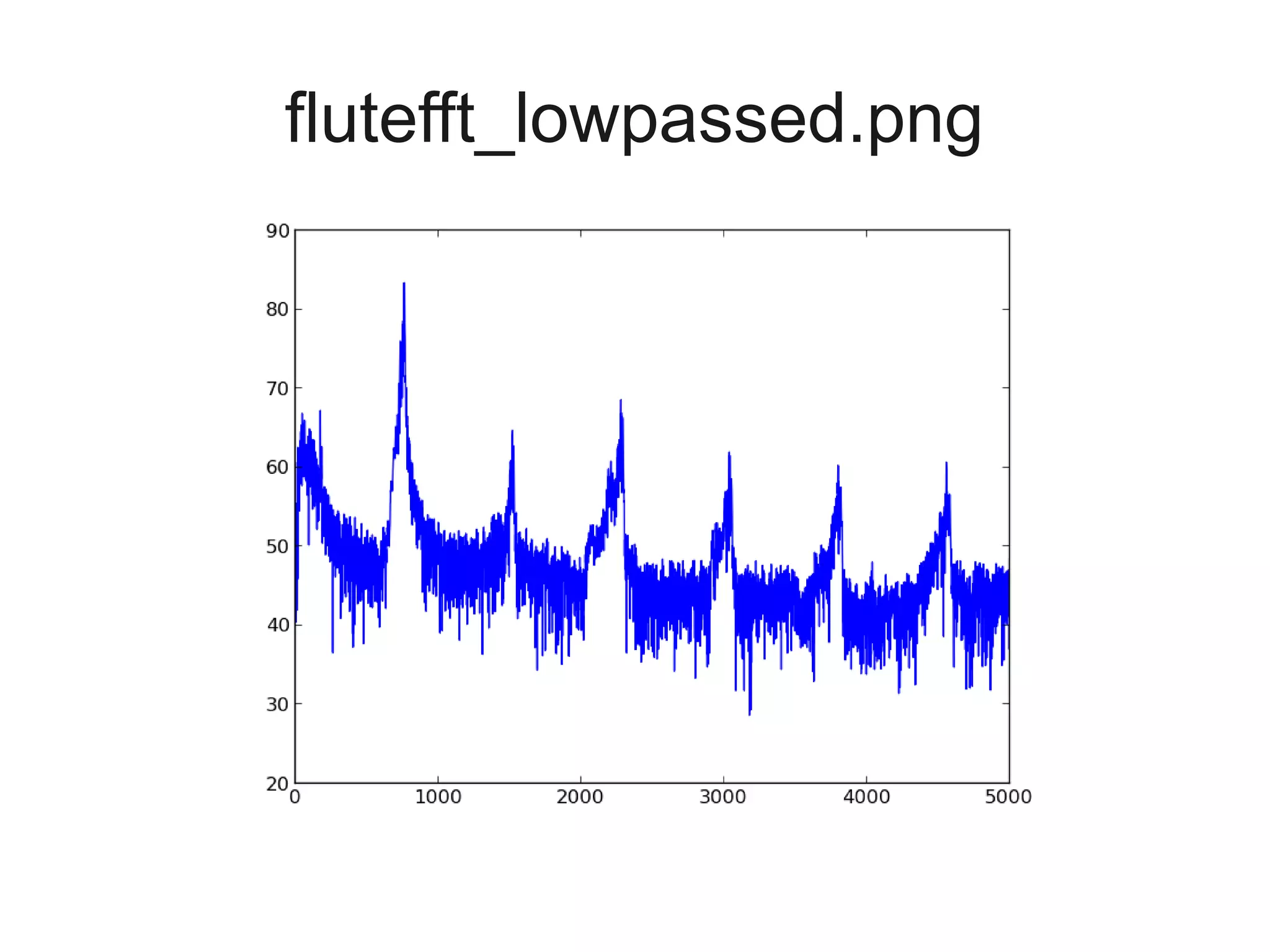
63. Implement and plot the low-pass
filter in the frequency domain...
# zero out all frequencies above
# the 5000th index
# (BONUS: what frequency does this
# correspond to?)
flutefft[5000:] = 0
# plot on decibel (dB) scale
makegraph(10*log10(abs(flutefft)),
'flutefft_lowpassed.png')

64. flutefft_lowpassed.png

65. Going from frequency back to time
domain so we can listen
reflute = fft.irfft(flutefft,
len(audio))
reflute_coerced = array(reflute,
dtype=int16) # coerce it
makewav(reflute_coerced,
'flute_lowpassed.wav', 44100)

66. What does the spectrogram of the
low-passed flute sound look like?
pyplot.clf()
sgram = specgram(audio)
pyplot.savefig('reflutespectro.png')

67. reflutespectro.png

68. Compare to flutespectro.png

69. Your turn
● Take some of your .wav files from earlier, and
try making...
● Low-pass or high-pass filters
● Band-pass, band-stop, or notch filters
● Filters with varying amounts of rolloff

70. Agenda
● Introduction
● Fourier transforms, spectrums, and spectrograms
● Playtime!
● SANITY BREAK
● Nyquist, sampling and aliasing
● Noise and filtering it
● (if time permits) formants, vocoding, shifting, etc.
● Recap: so, what did we do?

71. Formants

72. Formants
f1 f2
a 1000 Hz 1400 Hz
i 320 Hz 2500 Hz
u 320 Hz 800 Hz
e 500 Hz 2300 Hz
o 500 Hz 1000 Hz

73. Vocoding
http://en.wikipedia.org/wiki/Vocoder

74. Bode plot (high pass)

75. Another Bode plot...

76. Credits and Resources
● http://onlamp.com/pub/a/python/2001/01/31/numerically.html
● http://jeremykun.com/2012/07/18/the-fast-fourier-transform/
● http://lac.linuxaudio.org/2011/papers/40.pdf
● Farrah Fayyaz, Purdue University
● signalprocessingforaudiologists.wordpress.com
● Wikipedia (for images)
● Tons of Python library documentation