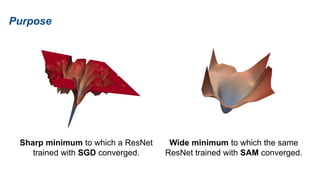
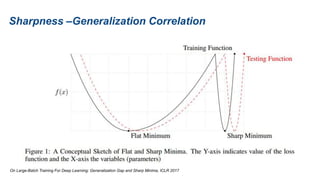
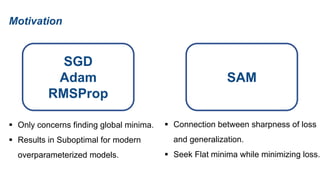
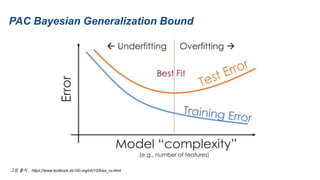
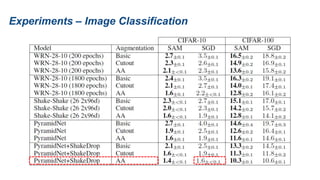
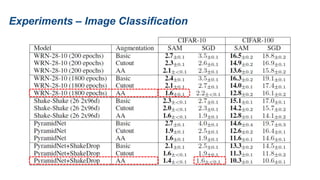
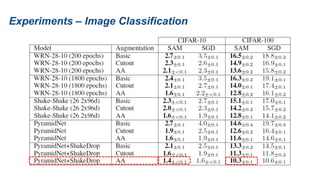
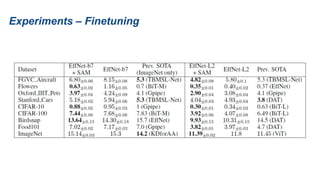
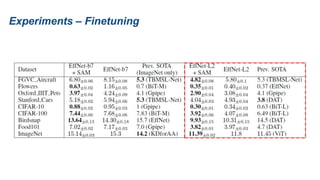
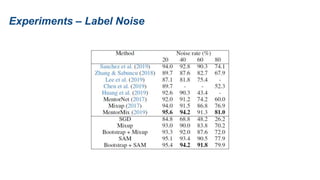
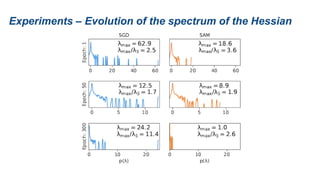
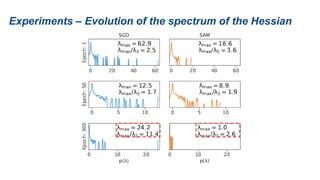
The document presents research on sharpness-aware minimization (SAM) as a method to improve generalization in deep learning, particularly for models trained with gradient descent methods like SGD. It discusses the correlation between loss sharpness and model generalization, explaining how SAM seeks to find flatter minima that enhance performance on various tasks including image classification and robustness to label noise. The approach involves minimizing upper bounds related to sharpness while also analyzing its effectiveness through experiments.

1. Sharpness-Aware Minimization for
Efficiently Improving Generalization
Presenter
이재윤
1
Fundamental Team
고형권, 김동희, 김준호, 김창연, 송헌, 이민경
Foret, Pierre, et al. "Sharpness-Aware Minimization for Efficiently
Improving Generalization." arXiv preprint arXiv:2010.01412 (2020).

2. Contents
1. Introduction
2. Sharpness-Aware-Minimization
3. Experiments

3. 1. Introduction

4. Purpose
Sharp minimum to which a ResNet
trained with SGD converged.
Wide minimum to which the same
ResNet trained with SAM converged.

5. Sharpness –Generalization Correlation
On Large-Batch Training For Deep Learning: Generalization Gap and Sharp Minima, ICLR 2017

6. Applied Task
1. Image Classification(CIFAR10, CIFAR100)
2. Finetuning
3. Robustness to Label Noise

7. Applied Task

8. 2. Sharpness-Aware-Minimization

9. Motivation
SGD
Adam
RMSProp
SAM
 Only concerns finding global minima.
 Results in Suboptimal for modern
overparameterized models.
 Connection between sharpness of loss
and generalization.
 Seek Flat minima while minimizing loss.

10. PAC Bayesian Generalization Bound

11. PAC Bayesian Generalization Bound
Probably the given classifier is Approximately Correct
for the test data.
(given a training dataset drawn i.i.d from distribution D)
Probably Approximately Correct

12. Probably the given classifier is Approximately Correct
for the test data.
(given a training dataset drawn i.i.d from distribution D)
H : model complexity
m : Training data 의 sample 수
PAC Bayesian Generalization Bound
Probably Approximately Correct

13. 그림 출처 : https://www.textbook.ds100.org/ch/15/bias_cv.html
PAC Bayesian Generalization Bound

14. PAC Bayesian Generalization Bound
Probably Approximately Correct
Bayesian Generalization Bound
D : test set

15. PAC Bayesian Generalization Bound
Probably Approximately Correct
Bayesian Generalization Bound
𝑆: 𝑡𝑟𝑎𝑖𝑛𝑖𝑛𝑔 𝑠𝑒𝑡
𝑤 ∶ 𝑐𝑙𝑎𝑠𝑠𝑖𝑓𝑖𝑒𝑟 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟𝑠
𝜌 ∶ 𝑣𝑎𝑙𝑢𝑒 𝑏𝑖𝑔𝑔𝑒𝑟 𝑡ℎ𝑎𝑛 0
𝜖 ∶ 𝑛𝑜𝑖𝑠𝑒 𝑎𝑟𝑜𝑢𝑛𝑑 0

16. PAC Bayesian Generalization Bound
Probably Approximately Correct
Bayesian Generalization Bound
h : strictly increasing function
𝑤: 𝑐𝑙𝑎𝑠𝑠𝑖𝑓𝑖𝑒𝑟 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟𝑠
𝜌 ∶ 𝑣𝑎𝑙𝑢𝑒 𝑏𝑖𝑔𝑔𝑒𝑟 𝑡ℎ𝑎𝑛 0

17. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization

18. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
=0

19. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term

20. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
Sharpness

21. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
Training Loss

22. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
Regularizer

23. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
L2-Regularizer

24. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term

25. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term

26. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term

27. Sharpness Aware Minimization
 Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term

28.  Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
 Minimize 𝐿𝑆
𝑆𝐴𝑀
Sharpness Aware Minimization

29.  Minimizing Upper Bound leads to Generalization
 Make explicit Sharpness term
 Minimize 𝐿𝑆
𝑆𝐴𝑀
Sharpness Aware Minimization
𝑆: 𝑡𝑟𝑎𝑖𝑛𝑖𝑛𝑔 𝑠𝑒𝑡
𝑤 ∶ 𝑐𝑙𝑎𝑠𝑠𝑖𝑓𝑖𝑒𝑟 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟𝑠
𝜌 ∶ 𝑣𝑎𝑙𝑢𝑒 𝑏𝑖𝑔𝑔𝑒𝑟 𝑡ℎ𝑎𝑛 0
𝜖 ∶ 𝑛𝑜𝑖𝑠𝑒 𝑎𝑟𝑜𝑢𝑛𝑑 0

30. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀

31.  Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
Sharpness Aware Minimization
1st order Taylor
expansion

32.  Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
Sharpness Aware Minimization

33.  Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
Sharpness Aware Minimization

34. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
 Dual Norm problem

35. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
 Dual Norm problem
 Substitute 𝜖 into 𝐿𝑆
𝑆𝐴𝑀

36. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
 Dual Norm problem
 Substitute 𝜖 into 𝐿𝑆
𝑆𝐴𝑀

37. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
 Dual Norm problem
 Substitute 𝜖 into 𝐿𝑆
𝑆𝐴𝑀

38. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
 Dual Norm problem
 Substitute 𝜖 into 𝐿𝑆
𝑆𝐴𝑀

39. Sharpness Aware Minimization
 Before minimizing, find 𝜖 which maximize 𝐿𝑆
𝑆𝐴𝑀
 Dual Norm problem
 Substitute 𝜖 into 𝐿𝑆
𝑆𝐴𝑀

40. Algorithm

41. Algorithm

42. 3. Experiments

43. Experiments – Image Classification

44. Experiments – Image Classification

45. Experiments – Image Classification

46. Experiments – Finetuning

47. Experiments – Finetuning

48. Experiments – Finetuning

49. Experiments – Label Noise

50. Experiments – Evolution of the spectrum of the Hessian

51. Experiments – Evolution of the spectrum of the Hessian

52. Thank you