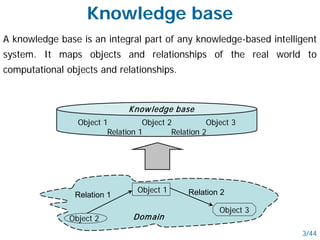
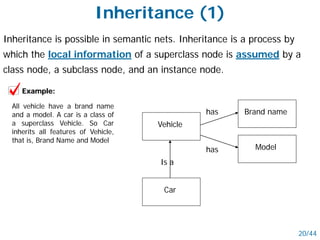
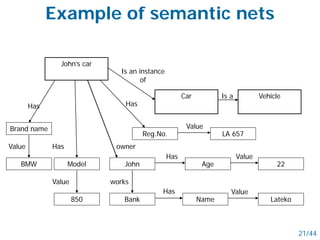
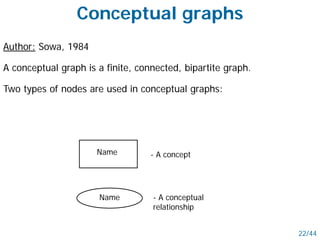
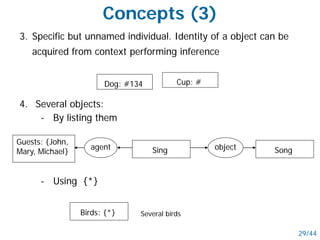
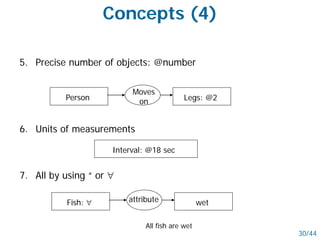
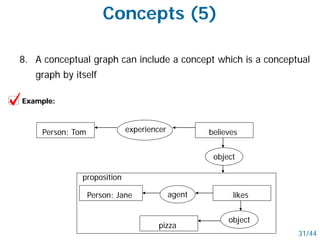
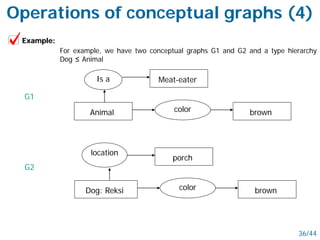
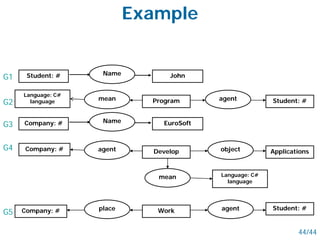
This document provides an overview of knowledge representation and networked schemes in artificial intelligence. It discusses several topics: - Knowledge representation is how knowledge is encoded in a computer-understandable form in an AI system's knowledge base. - Networked schemes like semantic nets and conceptual graphs represent knowledge using graphs with nodes for concepts and relationships. 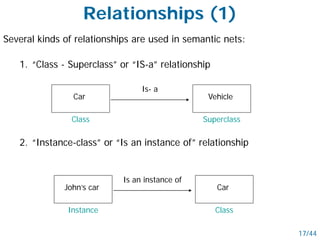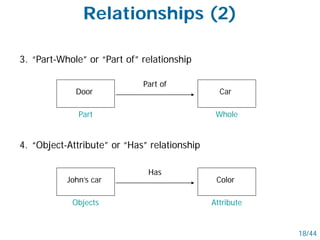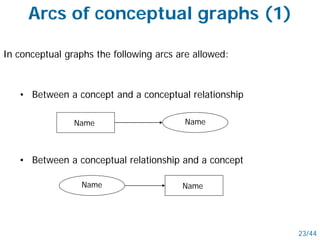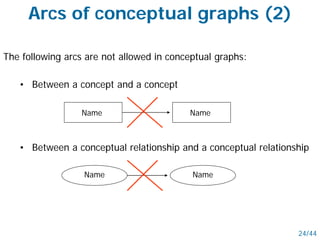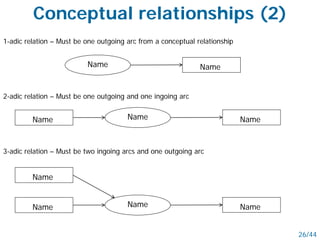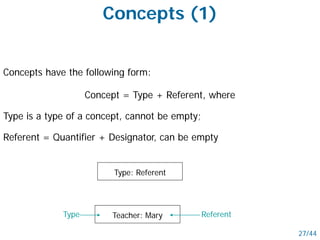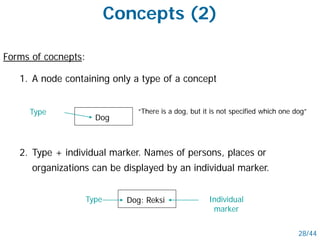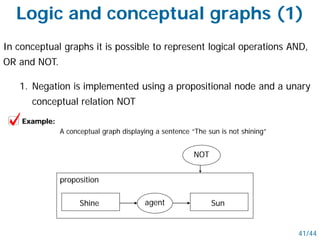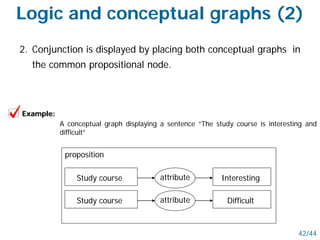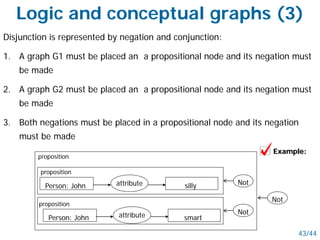- Semantic nets use nodes for concepts/objects and labeled arcs for relationships between nodes. Conceptual graphs also use concept and relationship nodes but have additional rules for node connections. 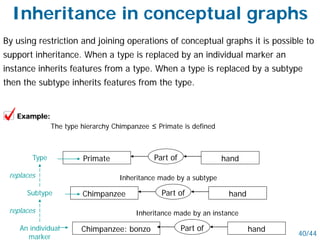- Both schemes allow inheritance of features through restriction and joining operations on the graphs. They can represent logical operations and support reasoning.

1. FUNDAMENTALS OF ARTIFICIAL
INTELLIGENCE
Riga Technical University
Faculty of Computer Science and Information Technology
Department of Systems Theory and Design
Dr.habil.sc.ing., professor Janis Grundspenkis, Dr.sc.ing., lecturer Alla Anohina-Naumeca
Department of Systems Theory and Design
Faculty of Computer Science and Information Technology
Riga Technical University
E-mail: {janis.grundspenkis, alla.anohina-naumeca}@rtu.lv
Address: Meza street 1/4- {550, 545}, Riga, Latvia, LV-1048
Phone: (+371) 67089{581, 595}
Lecture 7
KNOWLEDGE REPRESENTATION
AND NETWORKED SCHEMES

2. Knowledge representation
• Knowledge representation is the method used to
encode knowledge in an intelligent system’s
knowledge base.
• The object of knowledge representation is to
express knowledge in computer-tractable form, such
that it can be used to help intelligent system perform
well.
2/44

3. Knowledge base
A knowledge base is an integral part of any knowledge-based intelligent
system. It maps objects and relationships of the real world to
computational objects and relationships.
Object 1 Object 2 Object 3
Relation 1 Relation 2
Knowledge base
Domain
Object 1
Object 2
Object 3
3/44
Relation 1 Relation 2

4. But what is knowledge?
• Knowledge is an abstract term that attempts to capture an
individual’s understanding of a given subject.
• In the world of intelligent systems the domain-specific
knowledge is captured. Domain is a well-focused subject
area.
• Cognitive psychologists have formed a number of theories to
explain how humans solve problems. This work uncovered the
types of knowledge humans commonly use, how they
mentally organize this knowledge, and how they use it
efficiently to solve a problem.
4/44

5. Types of knowledge (1)
Declarative
knowledge
Concepts
Facts
Objects
Describes what is known
about a problem. This
includes simple statements
that are asserted to be
either true or false. This
also includes a list of
statements that more fully
describes some object or
concept (object-attribute-
value triplet).
5/44

6. Procedural
knowledge
Rules
Strategies
Agendas
Procedures
Describes how a
problem is solved.
This type of
knowledge provides
direction on how to do
something.
Types of knowledge (2)
6/44

7. Heuristic
Knowledge
Rules of
Thumb
Describes a rule-of-thumb
that guides the reasoning
process. Heuristic
knowledge is often called
shallow knowledge. It is
empirical and represents
the knowledge compiled by
an expert through the
experience of solving past
problems.
Types of knowledge (3)
7/44

8. Meta-
Knowledge
Knowledge
about the
other types
of
knowledge
and how to
use them
Describes knowledge
about knowledge. This
type of knowledge is used to
pick other knowledge that is
best suited for solving a
problem. Experts use this
type of knowledge to
enhance the efficiency of
problem solving by directing
their reasoning in the most
promising area.
Types of knowledge (4)
8/44

9. Structural
Knowledge
Rule sets
Concept
relationships
Concept to
object
relationships
Describes knowledge
structures. This type of
knowledge describes an
expert’s overall mental
model of the problem.
The expert’s mental
model of concepts, sub-
concepts, and objects is
typical of this type of
knowledge.
Types of knowledge (5)
9/44

10. Knowledge representation (1)
• In general, a representation is a set of conventions
about how to describe a class of things.
• A description makes use of the conventions of a
representation to describe some particular thing.
• The function of any representation scheme is to
capture essential features of a problem domain
and make that information available to a problem
solving procedure.
10/44

11. A representation consists of four fundamental
parts:
• A lexical part that determines which symbols are
allowed in the representation’s vocabulary.
• A structural part that describes constraints on
how the symbols can be arranged.
• A procedural part that specifies access
procedures that enable to create descriptions, to
modify them, and to answer questions using them.
• A semantic part that establishes a way of
associating meaning with the description.
Knowledge representation (2)
11/44

12. Knowledge representation schemes (1)
• Logical schemes
− Predicate calculus
− Propositional calculus
• Procedural schemes
• Structured schemes
− Scripts
− Frames
• Networked schemes
− Semantic nets
− Conceptual graphs
− IF..THEN.. rules
12/44
There are 4 schemes of knowledge representation:

13. Networked schemes use a graph to represent knowledge. Nodes of a
graph display objects or concepts in a domain, but arcs define
relationships between objects, their attributes and values of attributes.
13/44
Structured schemes extend networked representation by displaying
each node in a graph as a complex data structure.
In procedural schemes knowledge is represented as a set of
instructions for problem-solving. That allows to modify a knowledge
base easily and to separate a knowledge base from an inference
mechanism.
Logical schemes represent knowledge, using mathematical or
orthographic symbols, inference rules and are based on precisely
defined syntax and semantics.
Knowledge representation schemes (2)

14. Semantic nets
Author: Quillian, 1967
Idea: Concepts are a part of knowledge about world. People perceive
concepts and reason with them. Concepts are related with relationships
between them. Relationships between concepts form understanding of
people.
14/44

15. Definition of semantic nets
Semantic network is a knowledge representation schema that captures
knowledge as a graph. The nodes denote objects or concepts, their
properties and corresponding values. The arcs denote relationships
between the nodes. Both nodes and arcs are generally labelled (arcs
have weights).
Symbols of semantic nets:
Name
Name
- A concept
- A relationship
15/44

16. Nodes of semantic nets can represent:
• Concepts
• Objects
• Events
• Features
• Time
• etc.
16/44
Nodes of semantic nets

17. Relationships (1)
Several kinds of relationships are used in semantic nets:
1. “Class - Superclass” or “IS-a” relationship
Car
Is- a
Vehicle
Class Superclass
2. “Instance-class” or “Is an instance of” relationship
John’s car
Is an instance of
Car
Instance Class
17/44

18. Relationships (2)
3. “Part-Whole” or “Part of” relationship
Door
Part of
Car
Part Whole
4. “Object-Attribute” or “Has” relationship
John’s car
Has
Color
Objects Attribute
18/44

19. Relationships (3)
5. “Attribute-Value” or “Value” relationship
Color
Value
Red
Attribute Value
6. Logical relationships (and, or, not)
7. Linguistic relationships (examples: likes, owns, travels…)
19/44

20. Inheritance (1)
Inheritance is possible in semantic nets. Inheritance is a process by
which the local information of a superclass node is assumed by a
class node, a subclass node, and an instance node.
All vehicle have a brand name
and a model. A car is a class of
a superclass Vehicle. So Car
inherits all features of Vehicle,
that is, Brand Name and Model
Example:
20/44
Vehicle
Model
Brand name
Car
has
Is a
has

21. Example of semantic nets
21/44
owner
Is an instance
of
Is a Vehicle
Value
Value
Has
Has
Value
John’s car
Car
Bank
works
Name Lateko
John Age 22
LA 657Reg.No.
Brand name
ModelBMW
850
Has
Has
Has
Value
Value

22. Conceptual graphs
Author: Sowa, 1984
A conceptual graph is a finite, connected, bipartite graph.
Two types of nodes are used in conceptual graphs:
- A concept
- A conceptual
relationship
Name
Name
22/44

23. Arcs of conceptual graphs (1)
In conceptual graphs the following arcs are allowed:
• Between a concept and a conceptual relationship
Name Name
• Between a conceptual relationship and a concept
NameName
23/44

24. Arcs of conceptual graphs (2)
The following arcs are not allowed in conceptual graphs:
• Between a concept and a concept
Name
Name
• Between a conceptual relationship and a conceptual relationship
Name
Name
24/44

25. Conceptual relationships (1)
• Every conceptual relation r has a relation type t and a
nonnegative integer n called its valence.
• The number of arcs that belong to r is equal to its valence n. A
conceptual relation of valence n is said to be n-adic, and its
arcs are numbered from 1 to n.
• For every n-adic conceptual relation r, there is a sequence of n
concept types t1,...,tn, called the signature of r. A 0-adic
conceptual relation has no arcs, and its signature is empty.
• All conceptual relations of the same relation type t have the
same valence n and the same signature s.
• The term monadic is synonymous with 1-adic, dyadic with 2-
adic, and triadic with 3-adic. 25/44

26. 1-adic relation – Must be one outgoing arc from a conceptual relationship
NameName
2-adic relation – Must be one outgoing and one ingoing arc
3-adic relation – Must be two ingoing arcs and one outgoing arc
26/44
Conceptual relationships (2)
NameNameName
NameNameName
Name

27. Concepts (1)
Concepts have the following form:
Concept = Type + Referent, where
Type is a type of a concept, cannot be empty;
Referent = Quantifier + Designator, can be empty
27/44
Type: Referent
Teacher: MaryType Referent

28. 1. A node containing only a type of a concept
Concepts (2)
Forms of cocnepts:
“There is a dog, but it is not specified which one dog”
Dog
Type
2. Type + individual marker. Names of persons, places or
organizations can be displayed by an individual marker.
Dog: ReksiType Individual
marker
28/44

29. 3. Specific but unnamed individual. Identity of a object can be
acquired from context performing inference
Concepts (3)
Dog: #134
29/44
Cup: #
4. Several objects:
- By listing them
- Using {*}
Birds: {*} Several birds
Guests: {John,
Mary, Michael} Singagent object Song

30. 5. Precise number of objects: @number
Concepts (4)
Person
6. Units of measurements
Interval: @18 sec
30/44
Moves
on Legs: @2
7. All by using “ or ∀
Fish: ∀ attribute wet
All fish are wet

31. 8. A conceptual graph can include a concept which is a conceptual
graph by itself
Concepts (5)
believes
agent
object
experiencer
Person: Jane likes
Person: Tom
object
pizza
Example:
proposition
31/44

32. 9. Different combinations
Concepts (6)
Number: 18
Number: @18 18
32/44
Number: @18
There is a number 18
Number: {*} @5 18
There are eighteen numbers
There are eighteen numbers and all of
them are equal with 18
There are 5 numbers and all are equal
with 18

33. Operations of conceptual graphs (1)
Theory of conceptual graphs defines 4 operations:
• Copying
• Restricting
• Joining
• Simplifying
Copying allows acquiring of a new conceptual graph G1 which is
identical with the already existent conceptual graph G.
33/44

34. Restricting allows replacing of a concept node by its specialization.
Two cases are possible:
• Type can be replaced by an individual marker
• Type can be replaced by its subtype
Joining allows joining of two conceptual graphs if they have an
identical concept node.
Simplifying allows removing of one of two identical nodes of a
conceptual relation together with all its arcs.
34/44
Operations of conceptual graphs (2)

35. In order to apply the mentioned operations a type hierarchy must be
defined: if s and t are types of concepts and t≤s, then t is subtype of s.
35/44
Examples:
Manager ≤ Employee ≤ Person
Dog ≤ Animal
John ≤ Man ≤ Person
Operations of conceptual graphs (3)

36. Example:
For example, we have two conceptual graphs G1 and G2 and a type hierarchy
Dog ≤ Animal
brown
Is a
colorAnimal
Meat-eater
brown
location
colorDog: Reksi
porch
G2
G1
36/44
Operations of conceptual graphs (4)

37. Example:
Restricting operation can be applied to the graph G1 by replacing type Animal
with its subtype Dog: Reksi. A new graph G3 is acquired as a result.
G3
37/44
brown
Is a
colorDog: Reksi
Meat-eater
Operations of conceptual graphs (5)

38. Example:
Now we can join graphs G2 un G3, because they have an identical concept node
Dog:Reksi. A new graph G4 is acquired.
brown
Is a
color
Meat-eater
brown
location
colorDog:Reksi
porch
G4
38/44
Operations of conceptual graphs (6)

39. Example:
By simplifying the graph G4 a new graph G5 is acquired.
Is a Meat-eater
brown
location
colorDog:Reksi
porch
G5
39/44
Operations of conceptual graphs (7)

40. Inheritance in conceptual graphs
40/44
By using restriction and joining operations of conceptual graphs it is possible to
support inheritance. When a type is replaced by an individual marker an
instance inherits features from a type. When a type is replaced by a subtype
then the subtype inherits features from the type.
Part ofPrimate hand
Part ofChimpanzee hand
Part ofChimpanzee: bonzo hand
Example:
Inheritance made by a subtype
Inheritance made by an instance
Type
Subtype
An individual
marker
replaces
replaces
The type hierarchy Chimpanzee ≤ Primate is defined

41. Logic and conceptual graphs (1)
41/44
In conceptual graphs it is possible to represent logical operations AND,
OR and NOT.
1. Negation is implemented using a propositional node and a unary
conceptual relation NOT
agent
NOT
Shine Sun
proposition
Example:
A conceptual graph displaying a sentence “The sun is not shining”

42. 42/44
2. Conjunction is displayed by placing both conceptual graphs in
the common propositional node.
attributeStudy course Interesting
proposition
Example:
A conceptual graph displaying a sentence “The study course is interesting and
difficult”
attribute DifficultStudy course
Logic and conceptual graphs (2)

43. 43/44
Disjunction is represented by negation and conjunction:
1. A graph G1 must be placed an a propositional node and its negation must
be made
2. A graph G2 must be placed an a propositional node and its negation must
be made
3. Both negations must be placed in a propositional node and its negation
must be made
attributePerson: John silly
proposition
Example:
attribute smart
proposition
Not
proposition
Person: John
Not
Not
Logic and conceptual graphs (3)

44. mean
Example
Student: # John
Language: C#
language Program
Student: #
Company: # Applications
44/44
Student: #agent
Developagent object
WorkCompany: #
Name
mean
agentplace
G1
G2
G4
G5
Company: # EuroSoftName
G3
Language: C#
language