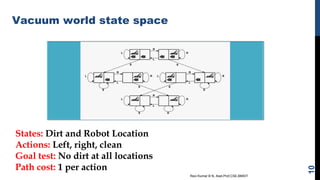
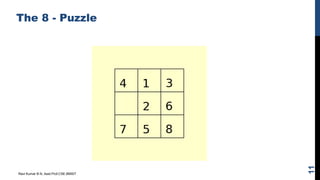
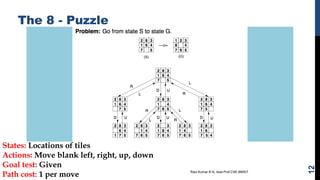
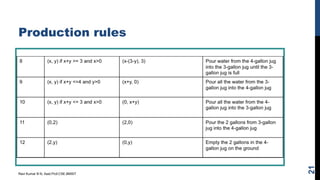
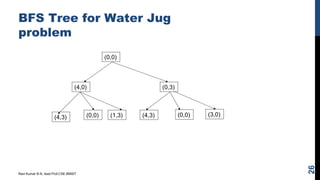
The document discusses state space search problems and techniques for solving them. It defines state space search as a process of considering successive configurations or states of a problem instance to find a goal state. Various search techniques like breadth-first search, depth-first search, and heuristic search are described. It also discusses problem characteristics that help determine the most appropriate search method, such as whether a problem can be decomposed or solution steps ignored/undone. Examples of search problems like the 8-puzzle, chess, and water jug problems are provided to illustrate state space formulation and solutions.






























![Blocks World Problem
Non Decomposable
Ravi Kumar B N, Asst.Prof,CSE,BMSIT
37
Following
operators are
available:
CLEAR(x) [ block x
has nothing on it]-
> ON(x, Table)
CLEAR(x) and
CLEAR(y) ->
ON(x,y) [ put x on
y]
C
A B
A
B
C
Start: ON(C,A)
Goal:
ON(B,C) and
ON(A,B)
ON(B,C)
ON(B,C) and ON(A,B)
ON(B,C)
ON(A,B)
CLEAR(A) ON(A,B)
CLEAR(A) ON(A,B)](https://image.slidesharecdn.com/pptugai02-180829053110/85/Problems-Problem-spaces-and-Search-37-320.jpg)






















