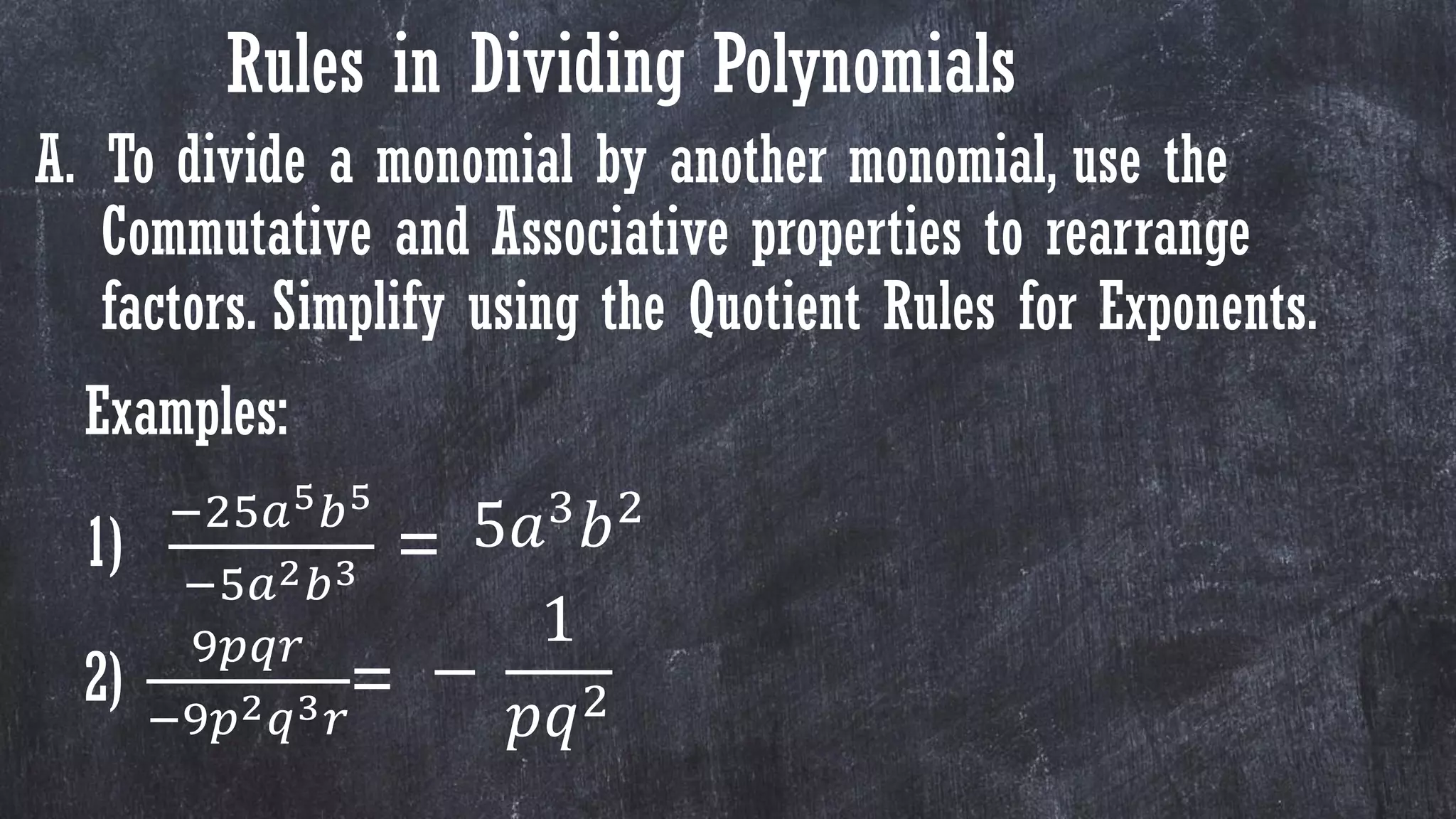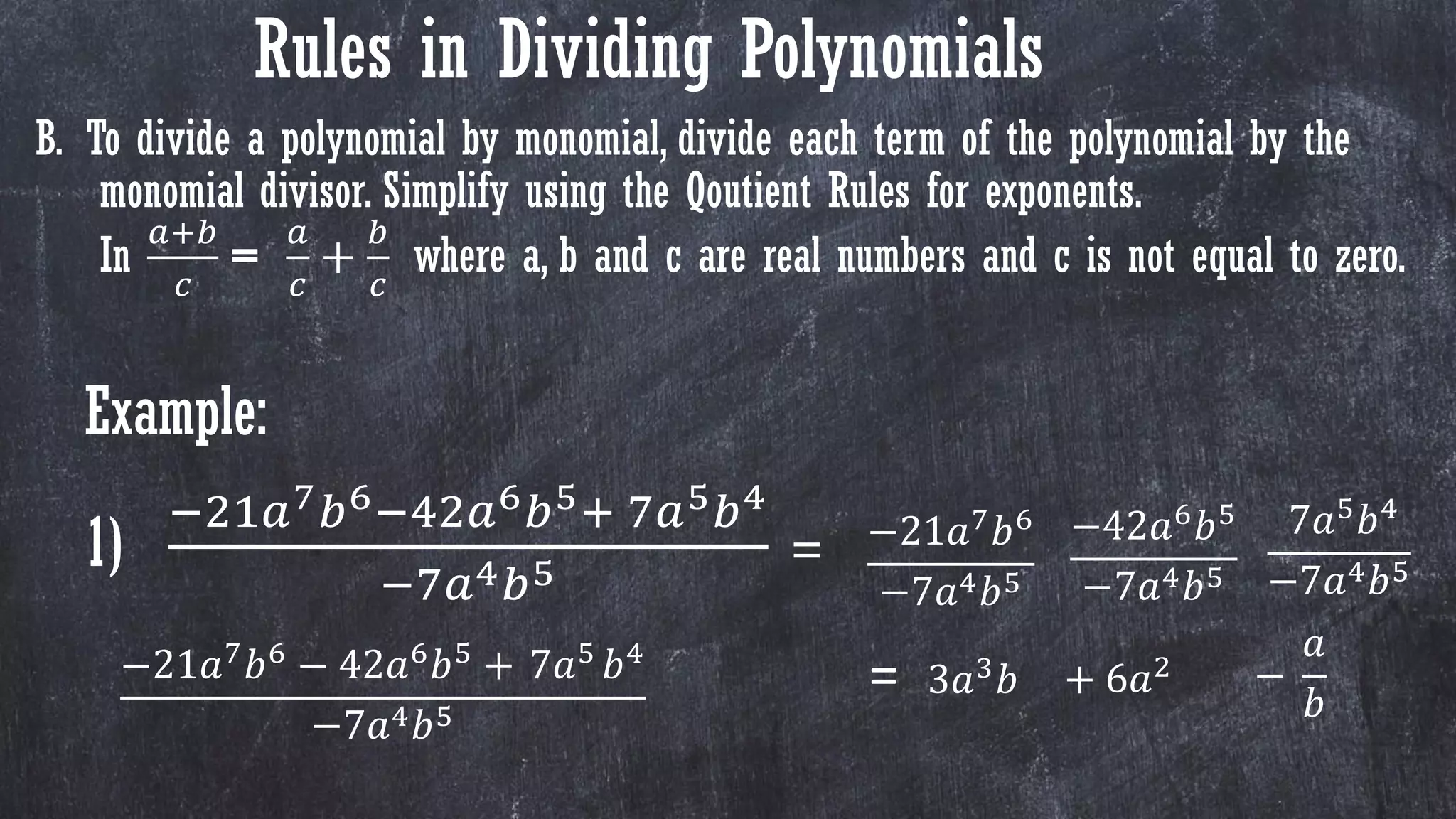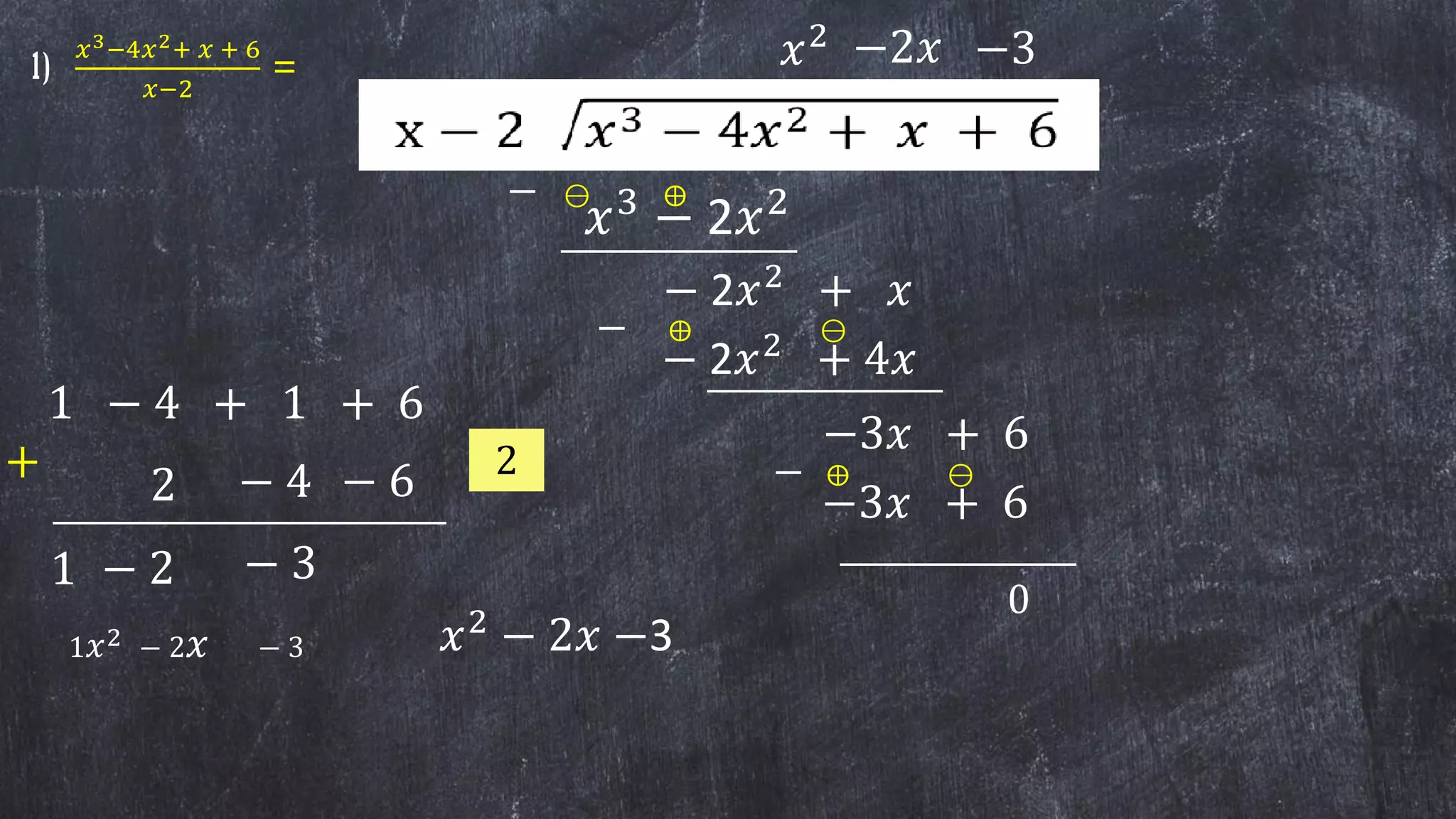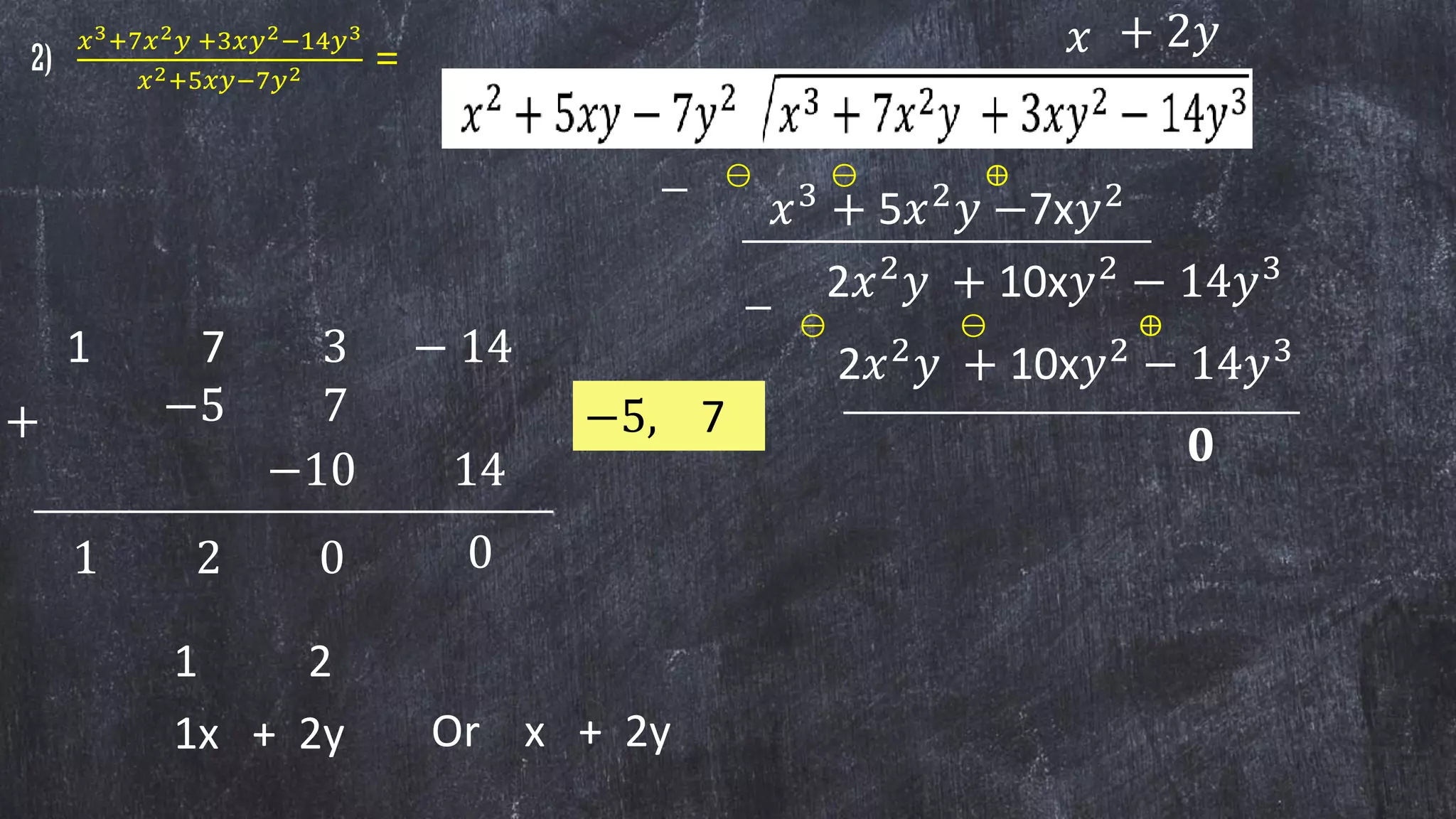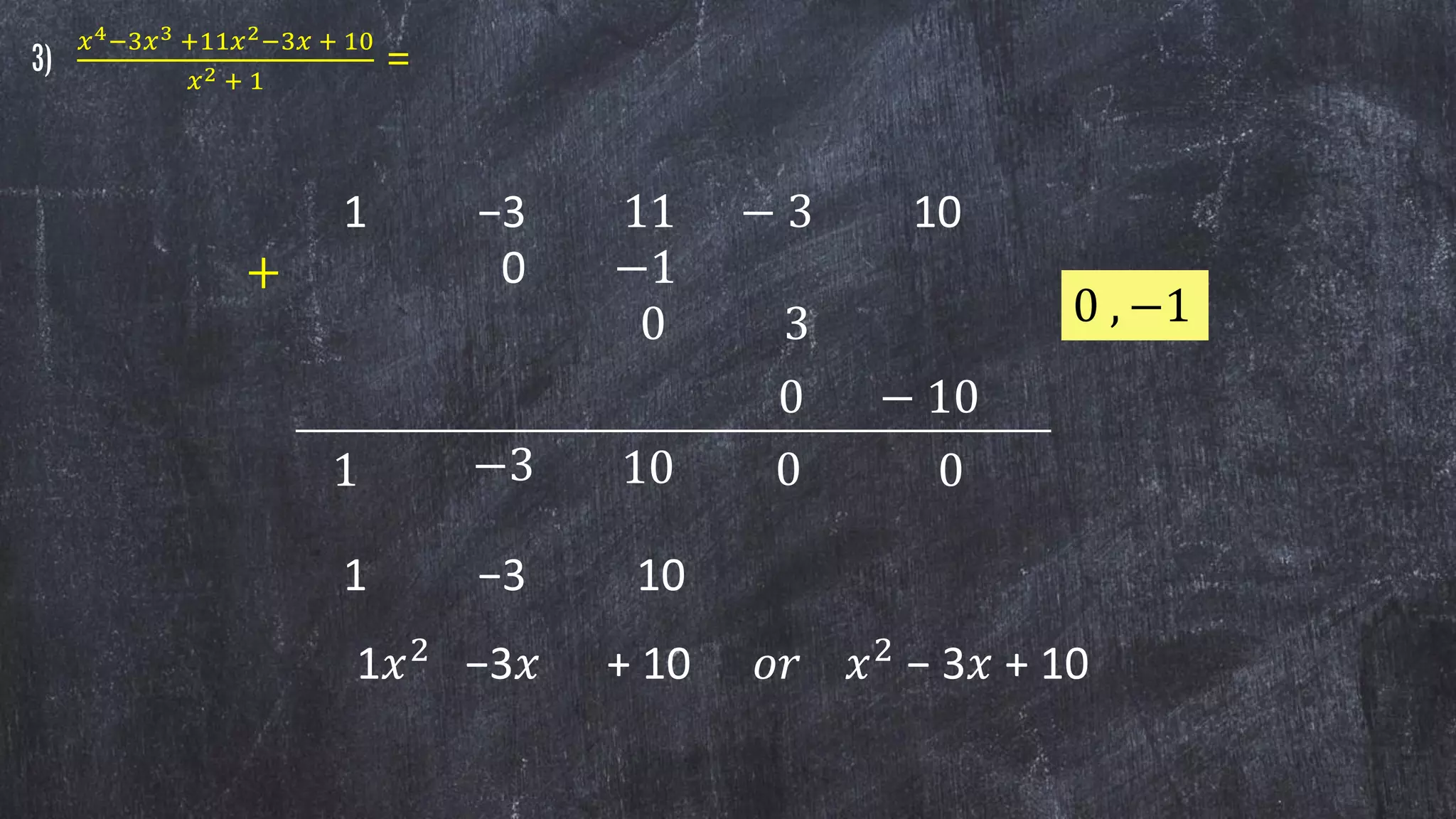1) The document discusses rules for dividing polynomials, including: dividing monomials by monomials using exponent rules; dividing polynomials by monomials by dividing each term; and dividing polynomials by polynomials using long division. 2) It provides examples of dividing polynomials in different forms such as monomial by monomial, polynomial by monomial, and polynomial by polynomial. 3) The goal is for students to learn how to divide polynomials in various scenarios and solve related problems.

2. :
In this lesson, students should be able to:
1) divide polynomials such as;
a) monomial by monomial,
b) polynomial by monomial,
c) polynomial by polynomial,
2) solve problems involving dividing polynomials.
2

3. A. To divide a monomial by another monomial, use the
Commutative and Associative properties to rearrange
factors. Simplify using the Quotient Rules for Exponents.
−
1
𝑝𝑞2
Examples:
1)
−25𝑎5 𝑏5
−5𝑎2 𝑏3 =
2)
9𝑝𝑞𝑟
−9𝑝2 𝑞3 𝑟
=
5𝑎3 𝑏2
Rules in Dividing Polynomials

4. B. To divide a polynomial by monomial, divide each term of the polynomial by the
monomial divisor. Simplify using the Qoutient Rules for exponents.
In
𝑎+𝑏
𝑐
=
𝑎
𝑐
+
𝑏
𝑐
where a, b and c are real numbers and c is not equal to zero.
Example:
1)
−21𝑎7 𝑏6−42𝑎6 𝑏5+ 7𝑎5 𝑏4
−7𝑎4 𝑏5 = −21𝑎7 𝑏6
−7𝑎4 𝑏5
Rules in Dividing Polynomials
−42𝑎6
𝑏5
−7𝑎4 𝑏5
7𝑎5 𝑏4
−7𝑎4 𝑏5
−21𝑎7
𝑏6
− 42𝑎6
𝑏5
+ 7𝑎5
𝑏4
−7𝑎4 𝑏5
= 3𝑎3 𝑏 + 6𝑎2 −
𝑎
𝑏

5. C. To divide a polynomial by polynomial with more than one term, use a procedure
similar to long division.
Note: When using long division to divide polynomials, continue the division operation
until the remainder is 0 or the degree of the remainder is less than the degree
of the divisor.
Arrange the term with x in a descending order and the terms
with y in ascending order.
Example:
1)
𝑥3−4𝑥2+ 𝑥 + 6
𝑥−2
=
Rules in Dividing Polynomials

7. 1)
𝑥3−4𝑥2+ 𝑥 + 6
𝑥−2
= 𝑥2
𝑥3
− 2𝑥2
− 2𝑥2
+ 𝑥
−
⊖ ⨁
−2𝑥
− 2𝑥2
+ 4𝑥
_______________
−
−3𝑥 + 6
2
−3𝑥 + 6_________________________
⨁ ⊖−
−3
_______________
⨁ ⊖
1 − 4 + 1 + 6
_______________
0
1
2
− 2
− 4
− 3
− 6
1 𝑥2 − 2 𝑥 − 3 𝑥2
− 2𝑥 −3
+

8. 𝑥
𝑥3
+ 5𝑥2
𝑦 −7x𝑦2
2𝑥2
𝑦 + 10x𝑦2
− 14𝑦3
−
⊖ ⊖ ⨁
+ 2𝑦
2𝑥2
𝑦 + 10x𝑦2
− 14𝑦3
__________________________
−
0
_____________________________
2)
𝑥3+7𝑥2 𝑦 +3𝑥𝑦2−14𝑦3
𝑥2+5𝑥𝑦−7𝑦2 =
⊖ ⊖ ⨁
1 7 3 − 14
00
−5, 7
_________________________________
1
−5 7
−10 14
2
+
0 0
1 2
1x + 2y Or x + 2y

9. 3)
𝑥4−3𝑥3 +11𝑥2−3𝑥 + 10
𝑥2 + 1
=
1 −3 11 − 3 10
0 , −1
________________________________________________
1
0 −1
0 3
−3
+
10 0
1 −3 10
0 − 10
0
1𝑥2
−3𝑥 + 10 𝑜𝑟 𝑥2
− 3𝑥 + 10