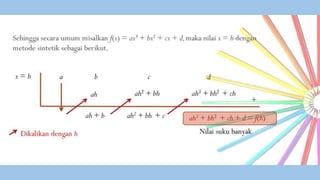
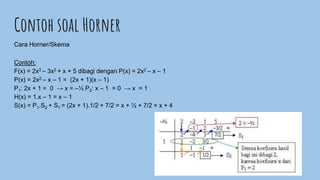
Polinomial adalah suatu bentuk matematika yang memuat variable berpangkat. Dokumen ini membahas operasi aljabar pada polinomial seperti penjumlahan, pengurangan, kesamaan, dan identitas nilai suku banyak, serta cara memecahkan persamaan suku banyak melalui pembagian polinomial dan metode faktorisasi.