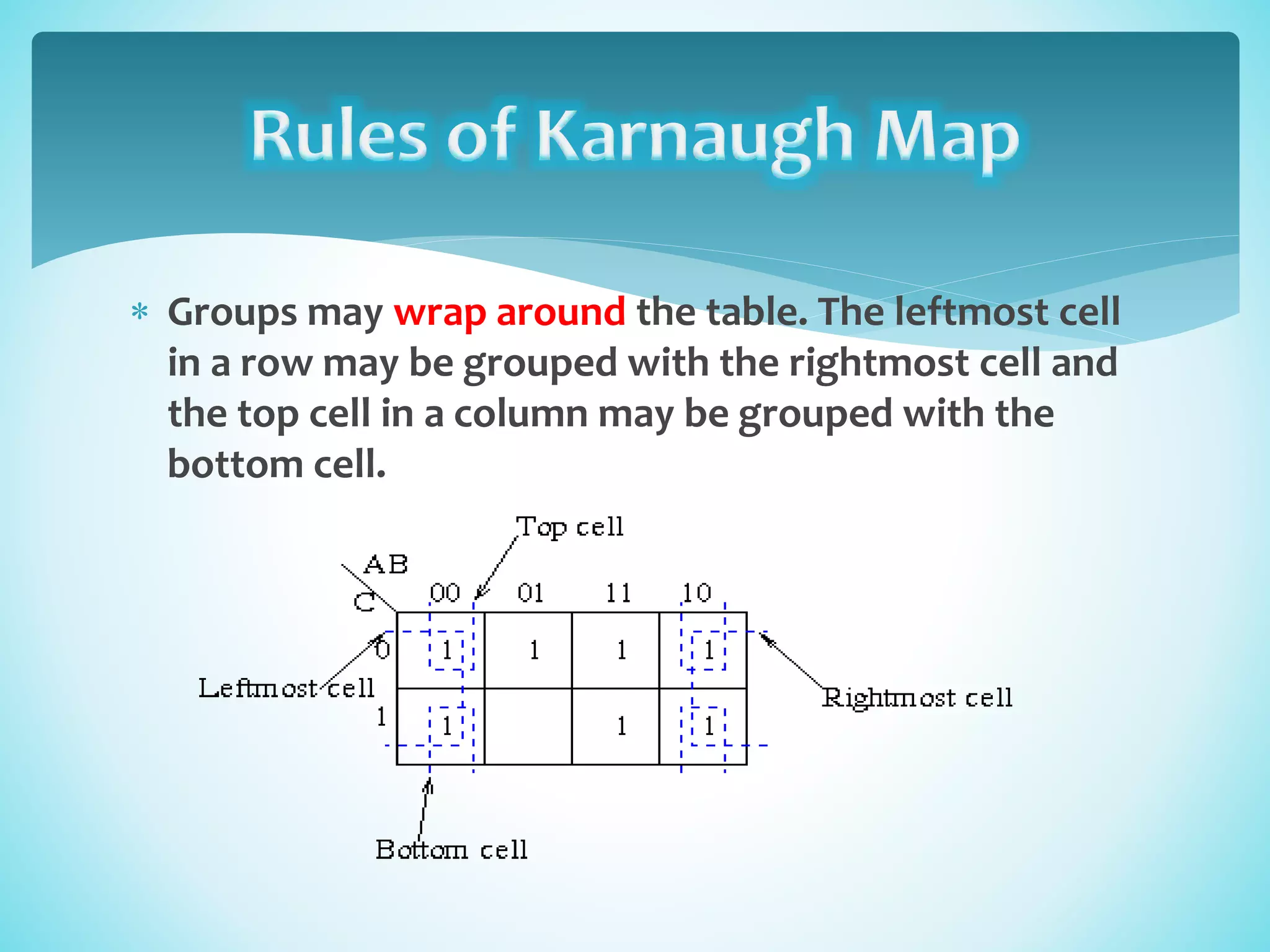
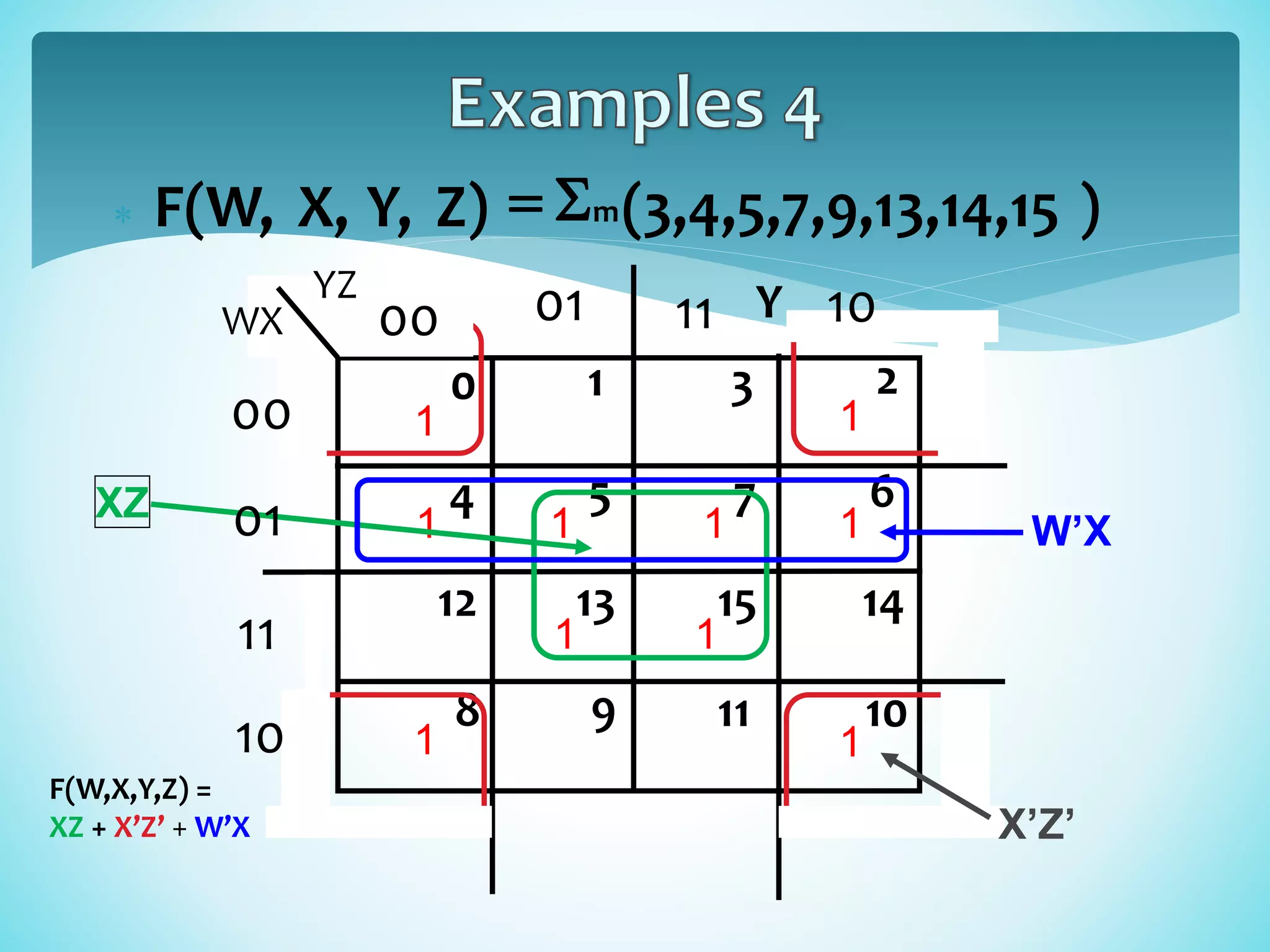
A Karnaugh map is a pictorial method for minimizing Boolean expressions without using Boolean algebra. It groups adjacent ones in a truth table together according to certain rules: groups cannot include zeros, must be horizontal/vertical not diagonal, contain a power of 2 number of cells, be as large as possible, include every one, can overlap, and wrap around. The goal is to find the minimum number of groups to simplify the expression.

3.  A Karnaugh map (K-map) is a pictorial method used to
minimize Boolean expressions without having to use
Boolean algebra theorems and equation manipulations. A
K-map can be thought of as a special version of a truth
table.
 Using a K-map, expressions with two to four variables are
easily minimized. Expressions with five to six variables are
more difficult but achievable, and expressions with seven
or more variables are extremely difficult to minimize
using a K-map.

4. The Karnaugh map uses the following rules for the
simplification of expressions by grouping together
adjacent cells containing ones.
 Groups can not include any cell containing a zero .

5.  Groups may be horizontal or vertical, but not
diagonal.

6.  Groups must contain 1, 2, 4, 8, or in general 2n cells.
That is if n = 1, a group will contain two 1's since 21 =
2.
If n = 2, a group will contain four 1's since 22 = 4.

7.  Each group should be as large as possible.

8.  Each cell containing a one must be in at least one
group.

9.  Groups may overlap each other.

10.  Groups may wrap around the table. The leftmost cell
in a row may be grouped with the rightmost cell and
the top cell in a column may be grouped with the
bottom cell.

11.  There should be as few groups as possible, as long as
this does not contradict any of the previous rules.

13.  No zeros allowed.
 No diagonals.
 Only power of 2 number of cells in each group.
 Groups should be as large as possible.
 Every one must be in at least one group.
 Overlapping allowed.
 Wrap around allowed.
 Fewest number of groups possible.

15. 0 1 0 0
1 1 0 1
00 01 11 10
0
1
ab
c
F=a’bc’+a’bc+a’b’c+ab’c
F=a’b+b’c
Gates : 10
Gates : 5

16. 0 1 1 0
1 1 1 0
00 01 11 10
0
1
ab
c
F=a’bc’+a’bc+abc’+abc+a’b’c
F=b+a’c
Gates : 12
Gates : 3

17. 1 1 1
1 1
1
00 01 11 10
00
01
ab
cd
11
10
F=a’bc’d+a’bcd+abc’d+abcd+a’b’c’d+abcd’
F=bd+a’c’d+abc
Gates : 15
Gates : 7

18. 
Y
8 9 1011
12 13 1415
0 1 3 2
5 64 7
1 1
1 11 1
1 1
1 1
XZ
W’X
00
X’Z’
F(W,X,Y,Z) =
XZ + X’Z’ + W’X
3,14,15 )(3,4,5,7,9,1Z)Y,X,F(W, mS=
11
11 1001
01
10
00
WX
YZ

19.  http://books.google.com
 http://en.wikipedia.org/wiki/Karnaugh_map
 http://www.ustudy.in
 http://www.ee.surrey.ac.uk
 http://www.ece.rice.edu