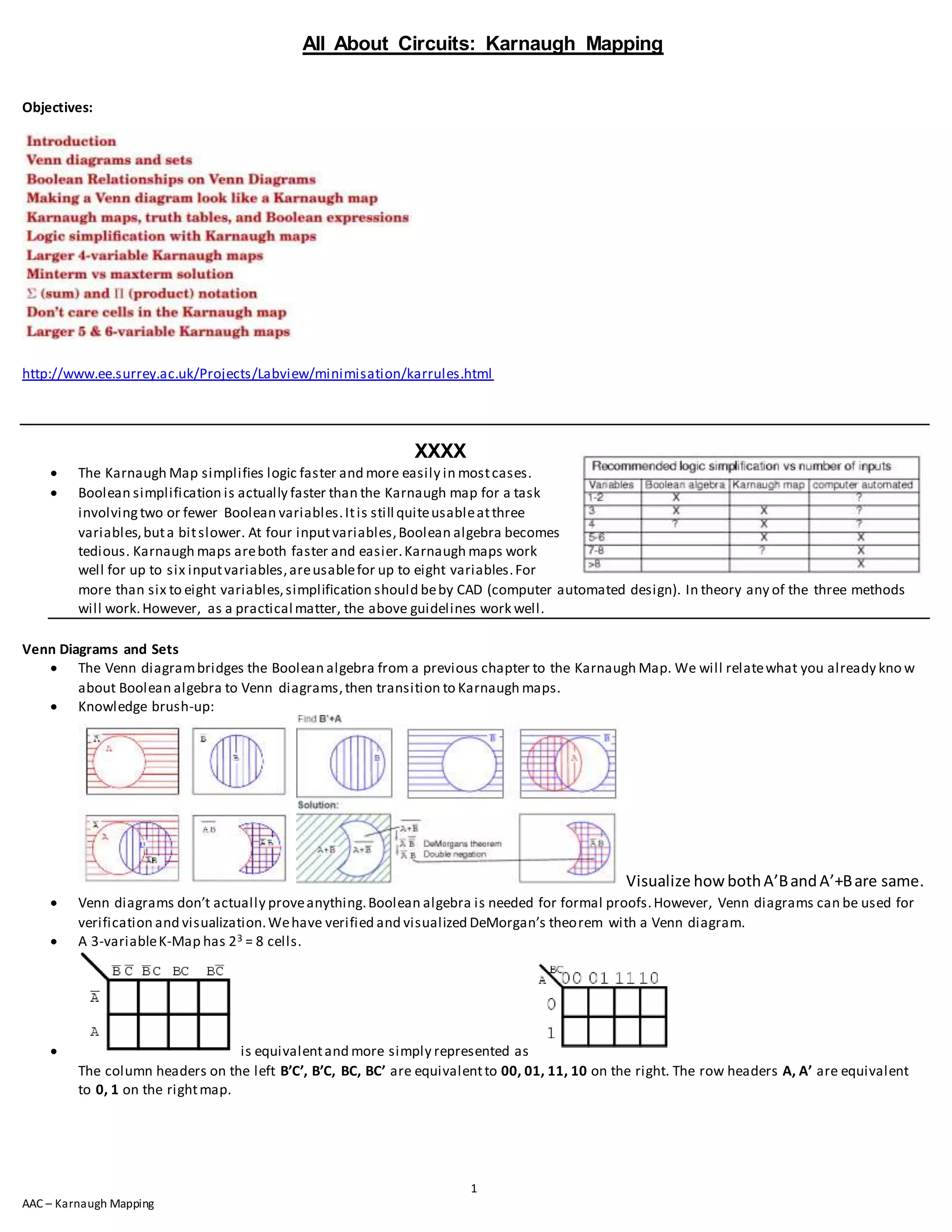
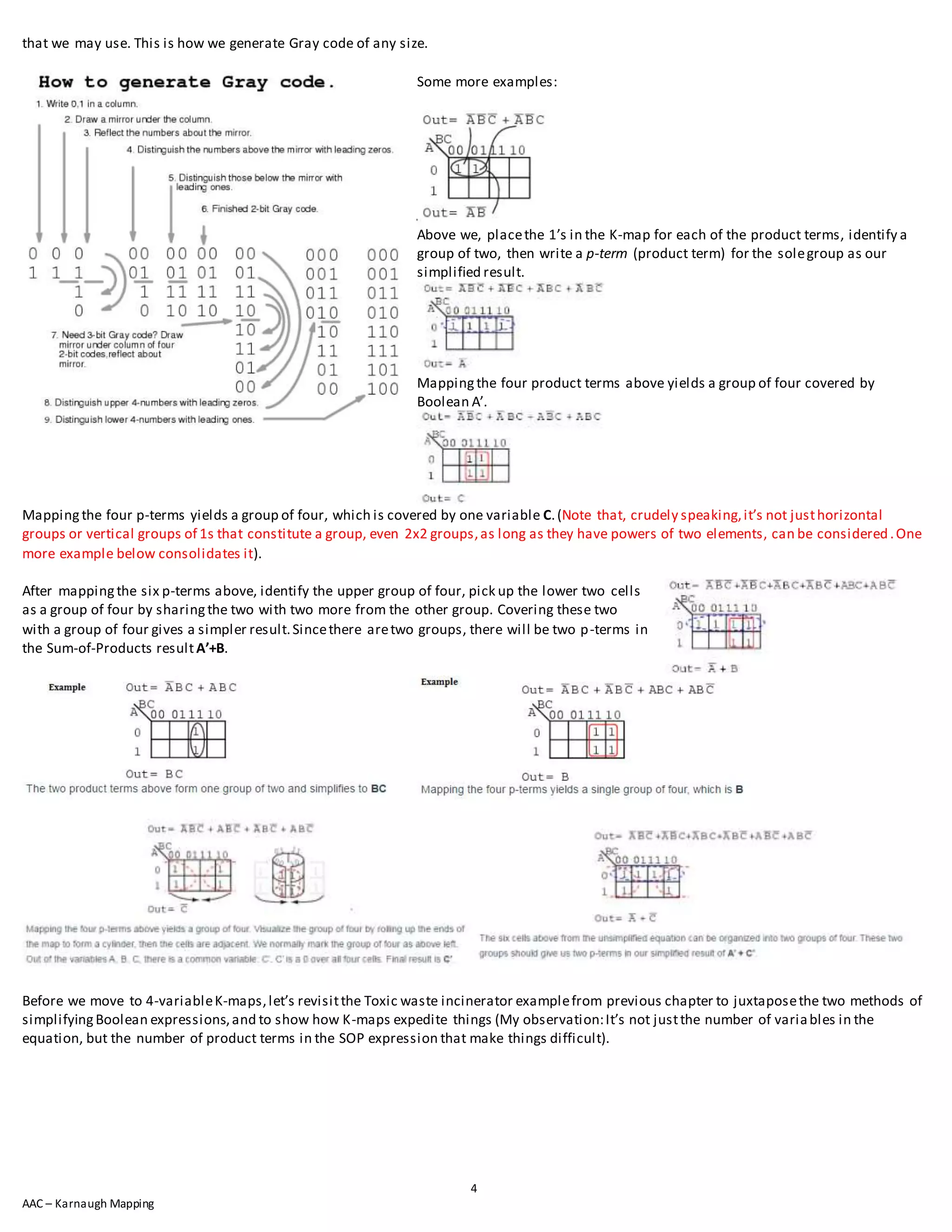
The document discusses Karnaugh mapping, which is a method for simplifying Boolean logic expressions. It provides guidelines for when different simplification methods like Boolean algebra or Karnaugh maps are best. Karnaugh maps are well-suited for problems with up to 6 variables and allow forming groups of cells to minimize logic. Examples show mapping logic terms to Karnaugh maps and identifying groupings to arrive at simplified expressions.

1. 1
AAC – Karnaugh Mapping
All About Circuits: Karnaugh Mapping
Objectives:
http://www.ee.surrey.ac.uk/Projects/Labview/minimisation/karrules.html
XXXX
 The Karnaugh Map simplifies logic faster and more easily in mostcases.
 Boolean simplification is actually faster than the Karnaugh map for a task
involvingtwo or fewer Boolean variables.Itis still quiteusableatthree
variables,buta bitslower. At four inputvariables,Boolean algebra becomes
tedious. Karnaugh maps areboth faster and easier.Karnaugh maps work
well for up to six inputvariables,areusablefor up to eight variables.For
more than six to eight variables,simplification should beby CAD (computer automated design). In theory any of the three methods
will work.However, as a practical matter, the above guidelines work well.
Venn Diagrams and Sets
 The Venn diagrambridges the Boolean algebra from a previous chapter to the Karnaugh Map. We will relatewhat you already kno w
about Boolean algebra to Venn diagrams,then transition to Karnaugh maps.
 Knowledge brush-up:
Visualize how bothA’BandA’+Bare same.
 Venn diagrams don’t actually proveanything.Boolean algebra is needed for formal proofs.However, Venn diagrams can be used for
verification and visualization.Wehave verified and visualized DeMorgan’s theorem with a Venn diagram.
 A 3-variableK-Map has 23 = 8 cells.
 is equivalentand more simply represented as
The column headers on the left B’C’, B’C, BC, BC’ are equivalentto 00, 01, 11, 10 on the right. The row headers A, A’ are equivalent
to 0, 1 on the rightmap.

2. 2
AAC – Karnaugh Mapping
 Karnaugh maps reduce logic functions morequickly and easily compared to
Boolean algebra.We define lowest cost as beingthe lowest number of gates with the
lowest number of inputs per gate.
 We showfive individual items above,which arejustdifferent ways of
representing the same thing: an arbitrary 2-inputdigital logicfunction.Firstis relay ladder
logic,then logic gates,a truth table, a Karnaugh map, and a Boolean equation. The pointis
that any of these are equivalent.
 The outputs of a relay ladder logic may be recorded in the truth table, or in the Karnaugh map.
Look at the Karnaugh map as beinga rearranged truth table.
 The outputs of a truth tablecorrespond on a one-to-one basisto Karnaugh map entries. Starting
at the top of the truth table, the A=0, B=0 inputs producean output α. The other truth table outputs β, χ, δ from inputs AB=01, 10, 11
are found at correspondingK-map locations.
 Which brings us to the whole point of the organizingthe K-map into a squarearray,cells with any Boolean variables in common need
to be closeto one another so as to present a pattern that jumps out at us. For cells αand χ they have the Boolean variable B’ in
common.
 Lest we forget to note down, the rulefor
adjacency of two cells (especially around
corners and top-bottom) is thatthe cells
must vary by the valueof one variable
only.
 If a truth table contains two 1s,the K-
map must have both of them.
 Diagonal cellsarenotadjacent.


3. 3
AAC – Karnaugh Mapping
Example: Fill inthe Karnaughmap for the Booleanexpressionbelow, thenwrite the Boolean
expressionfor the result.
Note:There will be a 1 entered for eachproduct term. The product term is the addressof the cell
where the 1 is entered.
Logic Simplification With Karnaugh Maps
The logic simplification examples thatwe have done so could have been performed with
Boolean algebra about as quickly.Real world logic simplification problems call for larger
Karnaugh maps so that we may do serious work.We will work some contrived examples in
this section,leavingmost of the real world applications for the Combinatorial Logic
chapter. By contrived, we mean examples which illustratetechniques.This approach will
develop the tools we need to transition to the more complex applications in theCombinatorial Logic chapter.We show our previous ly
developed Karnaugh map. We will usethe form on the right.
Note the sequence of numbers across thetop of the map. Itis not in binary sequence which would be 00, 01, 10,11. It is 00,01, 11 10, which is
Gray code sequence. Gray code sequence only changes one binary bitas we go from one number to the next in the sequence, unli kebinary.
That means that adjacentcells will only vary by one bit, or Boolean variable.This is whatwe need to organizethe outputs of a logic function so
that we may view commonality.Moreover, the column and row headings must be in Gray code order, or the map will notwork as a Karnaugh
map. Cells sharingcommon Boolean variables would no longer be adjacent,nor show visual patterns.Adjacentcells vary by only one bit
because a Gray code sequence varies by only one bit.If we sketch our own Karnaugh maps, we need to generate Gray code for an y sizemap

4. 4
AAC – Karnaugh Mapping
that we may use. This is how we generate Gray code of any size.
Some more examples:
Above we, placethe 1’s in the K-map for each of the product terms, identify a
group of two, then write a p-term (product term) for the solegroup as our
simplified result.
Mappingthe four product terms above yields a group of four covered by
Boolean A’.
Mappingthe four p-terms yields a group of four, which is covered by one variable C.(Note that, crudely speaking,it’s not justhorizontal
groups or vertical groups of 1s that constitute a group, even 2x2 groups,as long as they have powers of two elements, can be considered.One
more example below consolidates it).
After mappingthe six p-terms above, identify the upper group of four, pick up the lower two cells
as a group of four by sharingthe two with two more from the other group. Covering these two
with a group of four gives a simpler result.Sincethere aretwo groups, there will be two p-terms in
the Sum-of-Products resultA’+B.
Before we move to 4-variableK-maps,let’s revisitthe Toxic waste incinerator examplefrom previous chapter to juxtaposethe two methods of
simplifyingBoolean expressions,and to show how K-maps expedite things (My observation:It’s not justthe number of variables in the
equation, but the number of product terms in the SOP expression that make things difficult).

5. 5
AAC – Karnaugh Mapping
Larger 4-variable Karnaugh Maps
Knowing how to generate Gray code should allowus to build larger maps. Actually,all weneed to do is look at the
left to rightsequence across thetop of the 3-variablemap,and copy itdown the left sideof the 4-variablemap.See
below.
The followingfour variableKarnaugh maps illustratereduction of Boolean expressions
too tedious for Boolean algebra.Reductions could be done with Boolean algebra.
However, the Karnaugh map is faster and easier,especially if there aremany logic
reductions to do.
The above Boolean expression has seven product terms. They are mapped top to
bottom and left to righton the K-map above. For example, the firstP-term A’B’CD is
firstrow 3rd cell,correspondingto map location A=0, B=0, C=1, D=1. The other product terms are placed in a similarmanner. Encirclingthe
largestgroups possible,two groups of four areshown above. The dashed horizontal group corresponds to the simplified productterm AB. The
vertical group corresponds to Boolean CD. Sincethere aretwo groups, there will be two product terms in the Sum-Of-Products resultof
Out=AB+CD.
Now look at three VERY important examples below:
Example: Fold up the corners of the map below likeitis a napkin to make the four cells
physically adjacent.
The four cells abovearea group of four becausethey all havethe Boolean variables B’and D’ in
common. In other words,B=0 for the four cells,and D=0 for the four cells.The other variables
(A, B) are 0 in some cases,1 in other cases with respect to the four corner cells.Thus,these
variables (A,B) arenot involved with this group of four. This singlegroup comes out of the map
as one product term for the simplified result: Out=B’C’

6. 6
AAC – Karnaugh Mapping
Example: For the K-map below, roll the top and bottom edges into a cylinder formingeight
adjacentcells.The above group of eight has one Boolean variablein common: B=0. Therefore,
the one group of eight is covered by one p-term: B’. The original eightterm Boolean expression
simplifies to Out=B’
Example: The Boolean expression belowhas ninep-terms, three of which have three Booleans
instead of four. The difference is thatwhile four Boolean variableproductterms cover one cell,
the three Boolean p-terms cover a pair of cells each.
The six productterms of four Boolean variables map in the usual manner above as singlecells.Thethree Boolean variableter ms (three each)
map as cell pairs,which is shown above. Note that we are mappingp-terms into the K-map, not pullingthem out at this point.
For the simplification, weform two groups of eight. Cells in the corners are shared with both groups. This is fine.In fact, this leads to a better
solution than forming a group of eight and a group of four without sharingany cells. Final Solution is Out=B’+D’
Example: Below we map the unsimplified Boolean expression to the Karnaugh map.
Above, three of the cells form into a groups of two cells.A fourth cell cannotbe combined with
anything, which often happens in “real world” problems.In this case,the Boolean p-term ABCD is
unchanged in the simplification process.Result: Out= B’C’D’+A’B’D’+ABCD
Example: Often times there is more than one minimum cost solution to a simplification problem.Such
is the caseillustrated below.
Both results abovehave four product terms of three Boolean variables each.Both areequally valid minimal costsolutions.Thedifference in
the final solution isdueto how the cells aregrouped as shown above. A minimal costsolution is a valid logic design with the minimum number
of gates with the minimum number of inputs.
Example: Below we map the unsimplified Boolean equation as usual and forma group of four as a firstsimplification step.Itmay not b e
obvious how to pick up the remainingcells.

7. 7
AAC – Karnaugh Mapping
Pick up three more cells in a group of four, center above. There are still two cells remaining.the minimal costmethod to pick up those is to
group them with neighboringcells as groups of four as at above right. On a cautionary note, do not attempt to form groups of three.
Groupings must be powers of 2, that is,1, 2, 4, 8 ...
Example: Below we have another example of two possibleminimal costsolutions.Startby forminga coupleof groups of four after mappi ng
the cells.
The two solutions depend on whether the singleremainingcell is grouped with the firstor the second group of four as a group of two cells.
That cell either comes out as either ABC’ or ABD, your choice.Either way, this cell is covered by either Boolean product term. Final resultsare
shown above.
Example: Below we have an example of a simplification usingtheKarnaugh map at left or Boolean algebra at right. Plot C’ on the map as the
area of all cellscovered by address C=0, the 8-cells on the left of the map. Then, plot the singleABCD cell.That singlecell forms a group of 2-
cell as shown,which simplifies to P-term ABD, for an end resultof Out = C’ + ABD.
This (above) is a rareexample of a four variableproblemthat can be reduced with Boolean
algebra without a lot of work, assumingthatyou remember the theorems.
Mintermvs Maxterm Solution
So far we have been findingSum-Of-Product (SOP) solutions to logic reduction problems.For each of these SOP solutions,there is also a
Product-Of-Sums solution (POS),which could be more useful,depending on the application.
To be Cleared
 Instead of two overlappinggroups of 4 elements each, what if we have one of 4 elements (2 x 2) and one of two (horizontal)?

Associated Content
 We would not normally resortto computer automation to simplify a three input logic block.Wecould sooner solvethe problem with
pencil and paper. However, if we had seven of these problems to solve, say for a BCD (Binary Coded Decimal) to seven segment

8. 8
AAC – Karnaugh Mapping
decoder, we might want to automate the process.A BCD to seven segment decoder generates the logic signalsto drivea seven
segment LED (lightemitting diode) display.
 Examples of computer automated design languages for simplification of logic arePALASM, ABEL, CUPL, Verilog, and VHDL. These
programs accept a hardwaredescriptor languageinputfilewhich is based on Boolean equations and produce an output filedesc ribing
a reduced (or simplified) Boolean solution.Wewill notrequire such tools in this chapter. Let’s move on to Venn diagrams as an
introduction to Karnaugh maps.
Grey Area