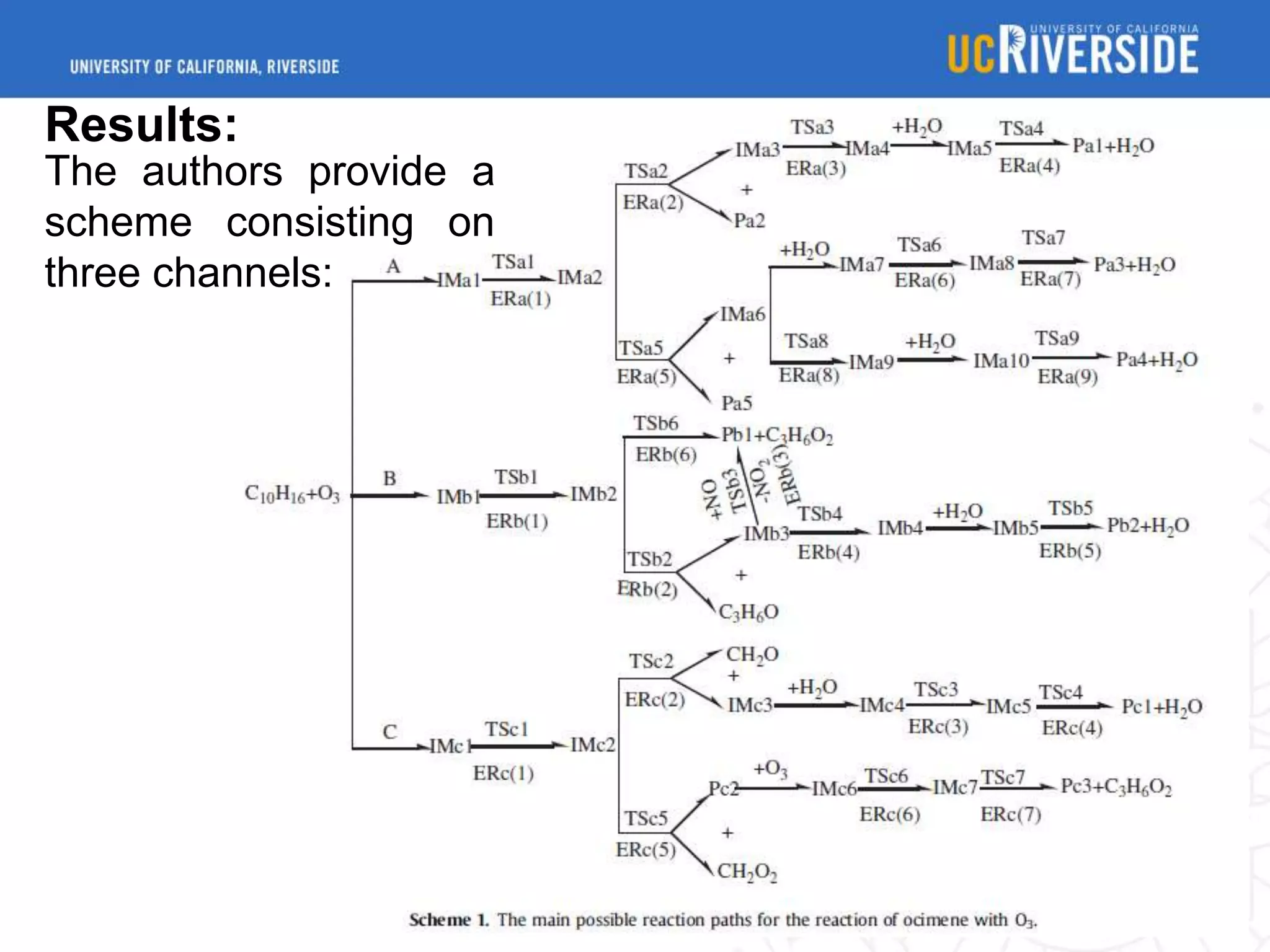
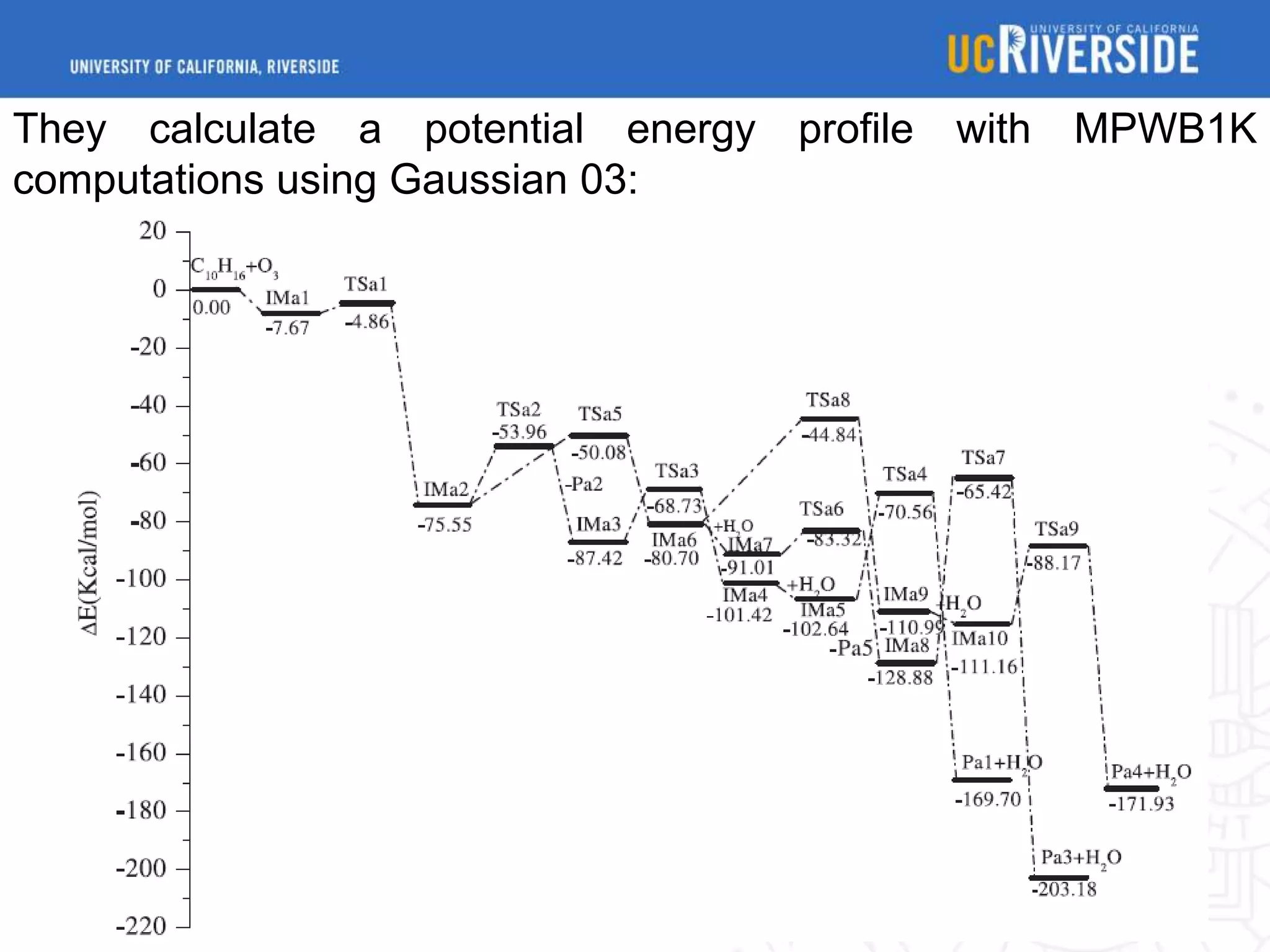
1) The document reports on a computational study of the chemical mechanism and kinetics of the ocimene ozonolysis reaction in the atmosphere. Rate constants and lifetimes of reaction intermediates were calculated. 2) RRKM theory and canonical variational transition state theory (CVTST) were used to derive kinetic equations and calculate microcanonical rate constants for the elementary reaction steps. 3) Results show ocimene has a short lifetime of 86 minutes, while some intermediates have longer lifetimes of days. The kinetic data provides insight into secondary organic aerosol formation from biogenic monoterpene oxidation.

1. Atmospheric Environment. 45, (2011), 6197-6203
Chemical mechanism and kinetic
study on the ocimene ozonolysis
reaction in atmosphere
Xiamin Sun[a,b], Jing Bai[a], Yuyang Zhao[a], Chenxi
Zhang[a], Yudong Wang[a], jingtian Hu[a]
a. Environment Research Institute, Shandong University, Jinan 250100, PR China
b. State Key Laboratory of Solid Lubrication, Lanzhou Institute of Chemical Physics,
Chinese Academy of Science, Lanzhou 730000, PR China

2. Main objective of the paper.
Obtain theoretical kinetic constants of ocimene
ozonolysis and its reaction pathway, in order to estimate
atmospheric lifetimes of the reaction species.

3. Background information:
Ocimene is a monoterpene released to
the atmosphere by the vegetation.
Reactions of biogenic monoterpenes
with ozone are responsible for a
significant amount of aerosol formation
in the atmosphere†.
†Hoffman
et. al. Journal of Atmospheric Chemistry, 12, (1997), 181-194.

4. Atkinson† describes ozonolysis in the following schemes:
†R.
Atkinson. Atmospheric
Environment, 34, (2000), 2
063-2101.

5. It is important to understand the elementary reactions
that form the mechanism for ozonolysis because some
intermediates react with (or produce) OH radicals, NOx,
SOx, carbon dioxide, and oxygen in the atmosphere.
E.g.
R. Atkinson. Atmospheric Environment, 34, (2000), 2063-2101.

6. Computational methods:
The paper is purely computational, therefore, no
experiments are made. The computational methods can
be divided in two parts:
-
Geometry optimization of intermediates and transition
states using a hybrid DFT model (MPWB1K) using
Gaussian 03. Used to get the potential energy profile.
-
Kinetic calculations using Rice-Ramsperher-KasselMarcus Theory, and Canonical Variational TST (with
the computer program PLYRATE v9.7)

7. Results:
The authors provide a
scheme consisting on
three channels:

8. Let’s focus on channel A:
ERa(1)
ERa(2)

9. ERa(3)
ERa(4)

10. ERa(5)
ERa(6)

11. ERa(7)
ERa(8)

12. ERa(9)

13. They calculate a potential energy
computations using Gaussian 03:
profile
with
MPWB1K

14. RRKM Theory is used for the following elementary reactions:
CVTST is used for the following isomerizations:

15. Derivation of kinetic equations:
RRKM Theory:
RRKM Theory traces its origins to Lindemann-Christensen
approach to unimolecular reactions:

16. Assuming steady state:
Hinshelwood modified this treatments by considering collision
theory:

17. Rice-Ramsperger-Kassel
dependence:
(RRK)
-
-
-
consider
the
energy
In order for A* to react, the
critical
energy
must
concentrate in one part of
the molecule
Free
energy
transfer
between
oscillators
is
assumed (loosely coupled
and separated).
The event that an oscillator
has the required energy
depends
on
statistical
factors

18. The probability of an oscillator to have enough energy is
calculated accordingly:
The rate constant for the conversion of the energized molecule
into the activated complex will be proportional to this
probability

19. The ratio between activation and de-activation rates of A now
follows a distribution function:
The “first-order” rate is now calculated by integration:
With a high pressure limit, it reduces to:

20. Energy diagram of the
different energies that are
involved in RRKM theory
www.chem.purdue.edu/mcluckey/.../2011_Prentice_SL_RRKM.pdf

21. Marcus follows the same mechanism but considers the energy
to be distributed in active (e.g vibrations) and inactive states
(e.g. translations) and merges TST with the RRK theory.
The first step is calculated as an equilibrium:

22. Assume that the activated complex to be in steady-state.
The ½ factor is accounted to lack of reversibility in the last step.
The rate constant of the energized molecule depends on the
energy of translation along the reaction coordinate:

23. Assume that the activated complex to be in steady-state.
The ½ factor is accounted to lack of reversibility in the last step.
The rate constant of the energized molecule depends on the
energy of translation along the reaction coordinate:

24. The active vibrational-rotational modes of the activated
complex cannot be assumed to be a continuous distribution.
Using a PIB approximation for the movement along delta:
After including a statistical factor l and
accounting for some changes in
rotational states

25. After integration, the cannonical “first-order” rate is obtained.
CVTST:
Using CTST we obtain the following expression:
CVTST obtains this canonical rate by integrating over all
energies:
The minimum k(T) obtained when the dividing surface is varied
is then chosen as the “closer” rate to the real rate constant.

26. The RRKM microcanonical k(3) rate is obtained from the
following.
The collision deactivation is calculated by the following:
The Beyer-Swinehart algorithm is used to calculate the
number of states and the density of states†. The POLYRATE
program is used for CVTST calculations‡.
†Moon
et al. J Am Soc Mass Spectrom, 18, (2007), 1063-1069.
‡Corchado et al., 2007. POLYRATE Version 9.7. University of Minnesota
Minneapolis.

27. The calculated rates are shown in this table:

28. The lifetimes are obtained:

29. Arrhenius formulas were fitted to the following T dependence:

30. Conclusions:
›
›
›
›
The authors that the lifetime for ocimene was 86 min
(short lifetime). IMa2 and IMa9 belong to middle
lifetime species (2.56 and 2.60 d). IMa4 and IMa8
belong to long lifetime species.
The authors conclude that the kinetic information
obtained is useful to understand the formation of
secondary organic aerosols.
Water acts as an activator for OH transfer and
promotes further reaction.
Oxidation occurs spontaneously once it is initiated by
ozone.