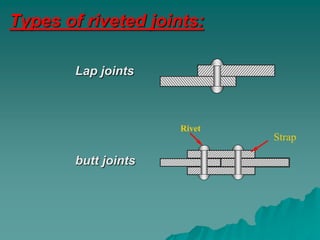
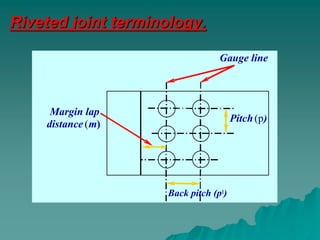
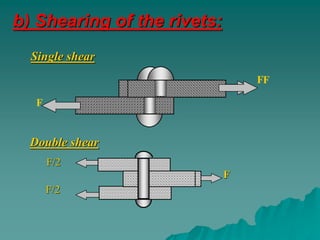
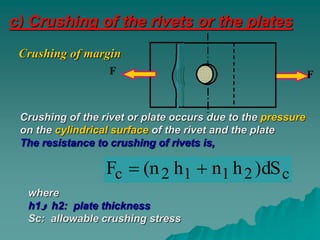
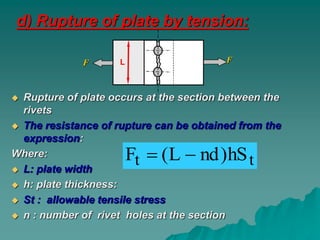
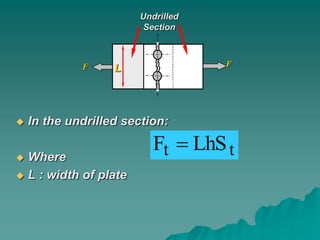
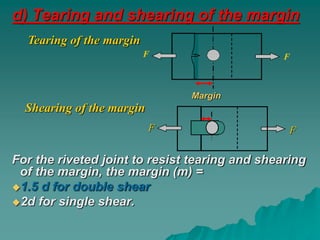
This document summarizes riveted joints, including their applications, components, types, and failure modes. Riveted joints are used to connect parts in pressure vessels, bridges, ships, airplanes, cranes, and buildings. A rivet consists of a head and shank. When forming a joint, rivets are inserted through holes in plates and the protruding end is hammered to form a second head. Common rivet materials include steel, nickel steel, brass, and aluminum. Key types of riveted joints are lap joints and butt joints. Failure can occur via bending of rivets or plates, shearing of rivets, crushing of rivets or plates, or rupture of

1. Riveted Joints

2. Riveting applications
Rivets
Types of riveted joints
Failure of riveted joints

3. Riveting applications:
Pressure vessels, boilers
tanks
Bridges
Hulls of ships
Airplanes
Cranes
buildings
Machinery in general

4. Rivets
A rivet is a round bar consisting of
head
shank.
The rivet blank is heated to a red glow
Inserted into the holes;
The head is held firmly against the
plate
The projecting end is formed into a
second head, called the point,
head
Point
Shank

5. Rivet material:
•Tough and ductile low carbon steel
•Nickel steel.
•Brass
•Aluminium

6. Types of riveted joints:
Lap joints
butt joints
Strap
Rivet

7. Riveted joint terminology.
(pPitch )
Gauge line
tBack pitch (p )
( )
Margin lap
distance m

8. Failure of riveted joints
 Bending of rivet or plate
FF
•In Lap connections the offset creates a moment
• M=Ft/2
•Bending moment causes complex deformations
and stresses
•In most cases this offset moment is neglected
•A suitable factor of safety is used.

9. b) Shearing of the rivets:
Single shear
Double shear
F
F/2
F/2
F
F
F

10. Joint strength in shear
Where,
 n1: :number of rivets in single shear
 n2: number of rivets in double shear
 Ss: allowable shear stress
 d : diameter of rivet
4
Sπd
)nn(2F s
2
12s 

11. c) Crushing of the rivets or the plates
Crushing of margin
F F
Crushing of the rivet or plate occurs due to the pressure
on the cylindrical surface of the rivet and the plate
The resistance to crushing of rivets is,
c2112c dS)hnh(nF 
where
h1‫و‬ h2: plate thickness
Sc: allowable crushing stress

12. d) Rupture of plate by tension:
 Rupture of plate occurs at the section between the
rivets
 The resistance of rupture can be obtained from the
expression:
Where:
 L: plate width
 h: plate thickness:
 St : allowable tensile stress
 n : number of rivet holes at the section
tt hS)ndL(F 
FF L

13.  In the undrilled section:
 Where
 L : width of plate
tt LhSF 
FF
Undrilled
Section
L

14. d) Tearing and shearing of the margin
For the riveted joint to resist tearing and shearing
of the margin, the margin (m) =
1.5 d for double shear
2d for single shear.
Shearing of the margin
Tearing of the margin
F F
F F
Margin

15. Example:
Fig.(3) shows a lap riveted joint, consists of two Rolled steel plates,
SAE 1020, of 0.5 in thickness. The plates are riveted together with
four rivets 0.375 inch in diameter of low carbon steel, SAE 1010.
Estimate the maximum value of the force F that the joint can stand
while considering a factor of safety equals 2 and the rivets are driven
by hand hammer.
F
F
0.5 in
4 in. 2
1
1

16. Solution
s
s
2
12s
f4
Sdπ
)nn(2F



24
10000.3750π
4F
2
s



Shearing of the rivets:
d = 0.375
fs = 2
n1 = 4
n2 =0
FS = 2209 lb
Load carrying member Type of stress Rivet-driving
power
Rivets acting in
single shear
Rivets acting in
double shear
Rolled steel, SAE 1020 Tension ….. 18000 18000
Rivets, SAE1010
Shear Power 13500 13500
Shear Hand 10000 10000
Crushing Power 24000 30000
Crushing Hand 16000 20000

17. Crushing of the rivets:
s
c2112
c
f
dS)hnh(n
F


2
160005.0375.04
Fc


FC = 6000 lb
Load carrying member Type of stress Rivet-driving
power
Rivets acting in
single shear
Rivets acting in
double shear
Rolled steel, SAE 1020 Tension ….. 18000 18000
Rivets, SAE1010
Shear Power 13500 13500
Shear Hand 10000 10000
Crushing Power 24000 30000
Crushing Hand 16000 20000

18. Rupture of plate by tension
s
t
t
f
hS)ndL(
F


2
180005.0)375.024(
Ft


Ft = 14625 lb
Load carrying member Type of stress Rivet-driving
power
Rivets acting in
single shear
Rivets acting in
double shear
Rolled steel, SAE 1020 Tension ….. 18000 18000
Rivets, SAE1010
Shear Power 13500 13500
Shear Hand 10000 10000
Crushing Power 24000 30000
Crushing Hand 16000 20000

19. Crushing of the plates
s
c2112
c
f
dS)hnh(n
F


2
36000375.05.04
Fc


FC = 13500 lb
Maximum value of F = 2209 lb
Load carrying member Type of stress Rivet-driving
power
Rivets acting in
single shear
Rivets acting in
double shear
Rolled steel, SAE 1020 Tension ….. 18000 18000
Rivets, SAE1010
Shear Power 13500 13500
Shear Hand 10000 10000
Crushing Power 24000 30000
Crushing Hand 16000 20000

20. Design procedure for structural joints
16
1h2d 
The following sequence of steps applies to the calculations
for structural joints:
• The load on each member is determined analytically or
graphically
• The shape and size of each member is determined based
on the load
• The diameter of the rivets is determined by the thickness
of the structural shapes apply the equation:

21. •The margin of the edge parallel to the load
d3ph16 
d5.11m 
d22m 
•The margin of the edge normal to the load
•Pitch limit:
where h is the thickness of the thinnest plate
used in the joint
•The number of rivets required is based upon the
shearing or crushing stress which ever determine the
cause of failure.
•The rivets in the joint are spaced in order to utilize the
material economically
•avoiding eccentric loading as far as possible

22. Thank You