DESIGN ANALYSIS OF UNIVERSAL JOINT SHAFT FOR ROLLING MILLS

PROJECT REPORT
ON
DESIGN ANALYSIS OF UNIVERSAL JOINT SHAFT FOR
ROLLING MILLS
Submitted to
RASHTRASANT TUKADOJI MAHARAJ NAGPUR UNIVERSITY
NAGPUR (M.S.)
in partial fulfillment of the Bachelor’s Degree in
MECHANICAL ENGINEERING
Submitted by
ANKIT ANAND (22) M. MUKESH (39)
MOHIT KATHOKE (46) SUGHOSH DESHMUKH (68)
VASUKARNA JAIN (74)
Under the Guidance of
Prof. G. R. NIKHADE
2013-2014
DEPARTMENT OF MECHANICAL ENGINEERING
SHRI RAMDEOBABA COLLEGE OF ENGINEERING & MGMT.
NAGPUR – 440 013

PROJECT REPORT
ON
ROLLING MILLS
Submitted to
RASHTRASANT TUKADOJI MAHARAJ NAGPUR UNIVERSITY
NAGPUR (M.S.)
in partial fulfillment of the Bachelor’s Degree in
MECHANICAL ENGINEERING
Submitted by
ANKIT ANAND(22) M. MUKESH (39)
VASUKARNA JAIN (74)
Under the Guidance of
Prof. G. R. NIKHADE
2013-2014
DEPARTMENT OF MECHANICAL ENGINEERING
NAGPUR – 440 013

NAGPUR – 440 013
CERTIFICATE
This is to certify that this is a bonafide record of project work entitled
ROLLING MILLS
Carried out by
VASUKARNA JAIN (74)
Of the Final Year B.E. MECHANICAL ENGINEERING during the
academic year 2013-2014 in partial fulfillment of requirement for the
award of Degree of BACHELOR OF ENGINEERING offered by the
RASHTRASANT TUKADOJI MAHARAJ NAGPUR UNIVERSITY,
NAGPUR (Maharashtra)
Prof. G. R. NIKHADE
Guide
Dr. K. N. Agrawal Dr.V. S. Deshpande
H.O.D. Principal

D E C L A R A T I O N
We the student of final year Mechanical engineering solemnly declare that, the
report of the Project work entitled Design Analysis Of Universal Joint Shaft
For Rolling Mills is based on our own work carried out during the course of
study under the supervision of Prof. G. R. Nikhade. We assert that the
statements made and conclusions drawn are an outcome of our research work.
We further certify that
i. The work contained in the Project is original and has been done by us
under the general supervision of our Guide.
ii. We have not reproduced this report or its any appreciable part from
any other literature in contravention of the academic thesis.
iii. We have conformed to the norms and guidelines given in the
concerned Ordinance of the RTM Nagpur University.
Date:
Submitted by,
VASUKARNA JAIN (74)

ACKNOWLEDGEMENTS
Apart from the efforts of the team, the success of any project depends largely on the
encouragement and guidelines of many others. We take this opportunity to express our
gratitude to the people who have been instrumental in the successful completion of this
Project.
Firstly we would like to thank Dr. V. S. DESHPANDE, Principal, RCOEM and Dr. K. N.
Agrawal, HOD, Mechanical Engineering Department. We would also like to show our
greatest appreciation to Prof. G. R. NIKHADE and Prof. R. U. PATIL. We can’t say thank
you enough for their tremendous support and help. We feel motivated and encouraged every
time we attend their meeting. Without their encouragement and guidance this report would
not have materialized.
We would also like to thank technical staff of the Department of Mechanical Engineering.
Our thanks are also due to Mr. K. S. Pande and Mr. N. M. Dadhe, Sunflag Iron and Steel
limited, Bhandara for their helpful advice and discussions.
Special thanks are due to all the staff of Sunflag Iron and Steel Limited, Bhandara, for their
continuous help during our project.
We wish to express our gratitude and love to our parents and siblings who were a constant
source of encouragement and support.
Finally, we thank the heavens from where we always receive inspiration and motivation and
with those blessings we were able to taste success in our endeavor.

CONTENTS
Chapter 1 Universal Joint 1
Chapter 2 Literature Review 5
Chapter 3 Problem identification and approach 22
Chapter 4 Process at BSM, Sunflag steel, Bhandara 24
Chapter 5 Rolling machine 26
Chapter 6 Basic calculations and assumptions 28
Chapter 7 Analysis for calculation of roll force and torque 34
Chapter 8 Validation of results 42
Chapter 9 CAD model of shaft and other parts 45
Chapter 10 Mesh generation 50
Chapter 11 Modal analysis 54
Chapter 12 Conclusions and suggestions 62
Chapter 13 Future scope 63
Appendix (Softwares used) 64
Appendix (About Sunflag Iron and Steel) 67
References 69

List of Figures:
Figure
No.
Figure Name Page No.
1.1 Universal Joint 1
1.2 Double Cardan Joint 2
1.3 Telescopic (Sliding) Universal Shaft 2
2.1 The universal joint (paradoxum) of Schott (1664) 6
2.2
‘Single’ Hooke's joints, with a cross-shaped interior member; with
a disc-shaped interior member; two commercial versions
6
2.3
‘Single’ Hooke's joints, with a cross-shaped interior member; with
a disc-shaped interior member; two commercial versions
7
2.4 Hooke's proposed driven azimuth mounting for a quadrant (1674) 7
2.5 Hooke's design for a universal with infinitely adjustable arms 7
2.6 The ‘double’ Hooke's joint 8
2.7 Fatigue Cracking Phenomenon 9
2.8 Life vs. failed bearing numbers 11
2.9
Position of the contact faces relative to the axis of rotation at the
trunion, a. side view, b. plan view
12
2.10 Closed eye 1 piece yoke 13
2.11 Split yoke 13
2.12 Split bearing eye 13
2.13 Block type 13
2.14 Integral face pads 14
2.15 Radial face spline 14
5.1 Shaft and roller setup 26
5.2 Parts of Rolling Mill 26
6.1
Incoming and outgoing section geometry of work piece at roll pass
(a):circle to oval, (b): oval to circle
32
6.2 Actual roller-billet geometry 33
7.1 Stress strain relation for steels 35
7.2 Temperature flow stress relation for steels at given strain rate 39
9.1 (top) Main Shaft assembly. (Bottom) Exploded view 45

9.2 Wobbler (Gear box side) 45
9.3 Wobbler (Roller side) 46
9.4 Eye Assembly 46
9.5 Exploded view of universal joint assembly 46
9.6 Yoke pin 47
9.7 Needle bearing with housing 47
9.8 Roller 48
9.9 Spider assembly 48
9.10 Complete shaft assembly 48
10.1 Geometry clean-up - Removal of fillets of minor detail 50
10.2 Geometry clean-up – Toggled edges 50
10.3 Mesh model of Shaft Assembly 51
10.4 Mesh model of Eye & Plate Assembly 51
10.5 Mesh model of Wobbler Assembly 51
10.6 Mesh model of Eye Plate 51
10.7 Mesh model of Shaft Assembly 52
10.8 3D Element Representation 53
10.9 Traditional Element Representation 53
11.1 Mode Shapes 54
11.2 SDOF system 55
11.3 MDOF system 56
11.4
Mode 1(top): Translation about X- axis
Mode 2(bottom): Translation about Y- axis
57
11.5 Mode 3- Translation about Z- axis 58
11.6 Mode 4- Rotation about X- axis 58
11.7 Mode 5- Rotation about Y- axis 58
11.8 Mode 6- Rotation about Z- axis 59
11.9 (Top) Normal Mode 1, (bottom) Normal Mode 2 59
11.10 (Top) Normal Mode 3, (Bottom) Normal Mode 4 60
11.11 Strained areas of eye plate 60
11.12 Loading of shaft, with fixing wobblers 61
11.13 Deflection of the shaft due to its self-weight 61

List of tables:
Table no. Title Page no.
6.1 Velocity, rpm and reduction data 28
6.2 Areas of the billet at inlet and exit of pass 31
9.1 Materials of various components 49
10.1 Element Quality Parameters 52
11.1 Natural frequency (by HyperMesh) 62
11.14 Stressed areas of pin and eye plate 62

CHAPTER 01 UNIVERSAL JOINT
1.1 Introduction
A universal joint, also known as universal coupling, U-joint, Cardan joint, Hardy
Spicer joint, or Hooke's joint is a joint or coupling in a rigid rod that allows the rod to
'bend' in any direction, and is commonly used in shafts that transmit rotary motion. It
consists of a pair of hinges located close together, oriented at 90° to each other, connected
by a cross shaft.
The term universal joint was used in the 18th
century and was in common use in the 19th
century. Edmund Morewood's 1844 patent for a metal coating machine called for a
universal joint, by that name, to accommodate small alignment errors between the engine
and rolling mill shafts. Lardner's 1877 Handbook described both simple and double
universal joints, and noted that they were much used in the line shaft systems of cotton
mills. Jules Weisbach described the mathematics of the universal joint and double
universal joint in his treatise on mechanics published in English in 1883.
19th
century uses of universal joints spanned a wide range of applications. Numerous
universal joints were used to link the control shafts of the Northumberland telescope at
Cambridge University in 1843. Ephriam Shay's locomotive patent of 1881, for example,
used double universal joints in the locomotive's drive shaft. Charles Amidon used a much
smaller universal joint in his bit-brace patented 1884. Beauchamp Tower's spherical,
rotary, high speed steam engine used an adaptation of the universal joint circa 1885.[1]
Figure 1.1: Universal Joint
Department Of Mechanical Engineering, RCOEM, Nagpur 1

1.2 Double Cardan Shaft
A configuration known as a double Cardan joint drive shaft partially overcomes the
problem of jerky rotation. This configuration uses two U-joints joined by an intermediate
shaft, with the second U-joint phased in relation to the first U-joint to cancel the changing
angular velocity. In this configuration, the angular velocity of the driven shaft will match
that of the driving shaft, provided that both the driving shaft and the driven shaft are at
equal angles with respect to the intermediate shaft (but not necessarily in the same plane)
and that the two universal joints are 90 degrees out of phase. This assembly is commonly
employed in rear wheel drive vehicles, where it is known as a drive shaft or propeller
(prop) shaft.
Even when the driving and driven shafts are at equal angles with respect to the
intermediate shaft, if these angles are greater than zero, oscillating moments are applied to
the three shafts as they rotate. These tend to bend them in a direction perpendicular to the
common plane of the shafts. This applies forces to the support bearings and can cause
"launch shudder" in rear wheel drive vehicles. The intermediate shaft will also have a
sinusoidal component to its angular velocity, which contributes to vibration and stresses.
Figure 1.3: Telescopic (Sliding) Universal Shaft
Figure 1.2: Double Cardan Joint

1.3 Advantages and disadvantages of universal shaft.
Universal Shafts are a preferred rotary motion transmission device because they:
 Eliminate alignment problems: Flexible Shafts have no need for the tight tolerances
that solid shafts require
 Provide greater design freedom : Limitless possibilities in positioning motor and
driven components
 Have higher efficiency: Flexible Shafts are 85%-95% efficient. Gears, U-Joints Belts
and Pulleys give much lower performance due to greater frictional losses
 Are light weight and powerful: Flexible Shafts have a good weight advantage over
other design solutions while transmitting greater power loads
 Have lower installation cost: Flexible Shafts install in minutes without special tools or
skills. Solid Shafts, Gears, Pulleys, and Universal Joints require precise alignment and
skilled mechanics for their installations.
 Reduce parts cost: Bearings and housings for Solid Shafts and Gears require precise
machining operations. Flexible Shafts eliminate the need for such demanding
tolerances and their excessive costs.
 Are easy to install: Need no special installation tools.
 Can be designed at the latter stages of a project: Unlike other rotary motion devices
that need to be designed around because of their rigidness, defined configurations, and
large mass. Flexible Shafts allow greater design freedom since engineers have only
one piece to work on, eliminating complex coordination of multiple pieces
1.4 Disadvantages
The Cardan joint suffers from one major problem: even when the input drive shaft axle
rotates at a constant speed, the output drive shaft axle rotates at a variable speed, thus
causing vibration and wear. Velocity and acceleration fluctuation increases with operating
angle. Other disadvantages are as follows:
• Lubrication is required to reduce wear.
• Shafts must lie in precisely the same plane.
• Backlash difficult to control.

1.5 Applications
 Aircraft
• Thrust Reverser Actuation System
• Variable Bleed Valve
• Flap & Slat Actuation Systems
 Automotive
 Pedal Adjuster
 Power Sliding Door
 Power Seat Track
 Tilt Steering
 Industrial
 Road Spike
 Power Sander
 Power Tools
 Medical
 Breast Biopsy
 MRI Drug Delivery
 Corneal Flap Maker
 Lawn & Garden
 String Trimmer

CHAPTER 02 LITERATURE REVIEW
To understand the scope of the project, the literature survey is a must. The literature
survey for this project is as follows.
2.1 Introduction
Robert Hooke is commonly thought of as the inventor of ‘Hooke's joint’ or the ‘universal
joint’. However, it is shown that this flexible coupling (based on a four-armed cross
pivoted between semi-circulars yoke attached to two shafts) was in fact known long before
Hooke's time but was always assumed to give an output exactly matching that of the input
shaft. Hooke carefully measured the relative displacements of the two axes, and found that
if one were inclined to the other, uniform rotation of the input produced a varying rate of
rotation of the output. Hooke's studies of the universal joint caused it to be identified with
his name, and it has ultimately proved far more important as a rotary coupling than as a
sundial analogue. More complex versions subsequently designed by Hooke included
provision for two basic couplings to be linked by an intermediate shaft. With appropriate
setting of phase and shaft angles this ‘double Hooke's joint’ could annul the variable
output velocity characteristic of the single universal. It has proved invaluable for modern
automotive transmissions.[20]
2.2 Angled couplings
Before proceeding further with applications of this device it is necessary to look back to an
earlier phase in the history of mechanisms. The need to transmit a rotary motion from a
primary shaft to a second shaft at an angle to the first (rather than directly in line or
parallel to it must have arisen repeatedly since ancient times, and been solved by a number
of anonymous artisans. An example cited by the Jesuit father Gaspar Schott was the 1354
clock in Strasbourg Cathedral, where the dial face was situated some way above and to the
side of the driving mechanism. Schott explains in a work published in 1664 that an angled
drive could have been achieved with bevel gears, but was more simply accomplished with
a chain of devices individually known as a paradoxum. He illustrates this mechanism with
the woodcut crediting it to an unpublished manuscript Chronometria Mechanica Nova by
a deceased anonymous author identified only as ‘Amicus’. The paradoxum can be seen to
be made up of the same two forks linked by a four-armed cross that characterize Hooke's
‘universal’.

2.3 The basic ‘universal joint’
Hooke's 1667 instrument was far too light and crude to have functioned satisfactorily as a
flexible coupling to transmit significant torque through an angle; although he does say that
it could ‘facilitate wheel-work and have other mechanical uses’. It was Hooke's study of
the motion of the universal joint, and his advocacy and application of the mechanism, that
led to its becoming commonly known as a ‘Hooke's joint’ to millwrights—at least in
England.
2.4 Mathematical analysis
Hooke was a competent mathematician, but the spherical trigonometry of his time was
insufficiently developed to permit 𝒕𝒂𝒏𝜷 = 𝒕𝒂𝒏𝜶 ∙ 𝒄𝒐𝒔𝝁 analysis of the kinematics of the
universal joint. Not until 1845 did Poncelet prove that where α is the angular position of
the input shaft, β is the angular position of the output shaft, μ is the inclination of one shaft
to the other—the ‘angle of articulation’.
2.5 Practical verification
2.5.1 Models
Working models of Hooke's joints were constructed to illustrate both the ‘cross’ and the
‘disc’ forms of interior member. They are shown in (Figure 2.2), along with commercial
examples in steel and acetal plastic.
Figure 2.2: ‘Single’ Hooke's joints. (From top to bottom)
with a cross-shaped interior member; with a disc-shaped
interior member; two commercial versions.
Figure 2.1: The universal joint (paradoxum) of Schott (1664)

2.5.2 Test rig
Apparatus for the study of couplings at various angles of articulation was built, and is
shown in (Figure 2.3). It was initially used to find the maximum angle of articulation
allowed by the various constructions shown in above figure. An inclination of 90° would
obviously not be possible as a result of geometrical constraint, but smaller angles are
limited by mechanical design when the tip of one fork contacts the base of the other near
its shaft.
Figure 2.3: Apparatus for studying the motion of single
or double Hooke's joints at various angles of
articulation.
2.6 Complex Hooke's joints
2.6.1 Single, but with adjustable arms
Hooke's first proposed application of the basic all-metal universal was to provide a drive
in azimuth (from a polar axis) to an astronomical quadrant mounted in such a way that its
own construction allowed manual adjustment in altitude (Figure 2.5). The simple universal
would not have worked in this situation.
Figure 2.4: Hooke's proposed
driven azimuth mounting for a
quadrant (1674).
Figure 2.5: Hooke's design for a
universal with infinitely
adjustable arms.

2.6.2 The double Hooke's joint
Hooke himself realized that there could be circumstances in which the periodic variation
in speed characterizing the standard form of coupling would be deleterious. His solution
was to employ two universals, one at each end of a common intermediate shaft, to give a
‘double’ joint (figure 2.6). The units may be assembled ‘in phase’, 90° out of phase, or in
any intermediate position. The orientation resulting in a transmitted motion 90° out of
phase with the input, combined with parallel input and output shafts (or equal angles of
inclination to the intermediate shaft) negates the variation, and the whole assembly is
commonly known nowadays as a constant-velocity coupling. They are available
commercially in a range of sizes. The addition of a splined assembly in the intermediate
shaft allows back and forth motion and has provided a coupling that, centuries after
Hooke's time, has proved enormously successful in the automobile. It allows power to be
transmitted from engine to wheels even when their relative positions are changing as a
result of going over bumps and hollows in the road.
2.7 Shaft failure modes
A shaft may fail by:
• Excessive lateral deflection, which causes items such as gears to move laterally
from their proper location, resulting in incorrect meshing.
• Torsional deflection, which destroys the precise angular relationship or "timing"
between sections of a mechanism.
• Wear may take place on bearing surfaces (journals) or other contact areas, such as
cams.
• Fracture. Unless the shaft was grossly under-designed, fracture usually occurs by
fatigue cracking. This is discussed below.
Figure 2.6: The ‘double’ Hooke's
joint.

2.7.1 The mechanism of fatigue cracking
Fatigue cracking occurs under conditions of repeated loading or cyclic loading. It is not
the magnitude of the load in itself which causes the failure. It is the cumulative effect of
many thousands, often millions, of repetitions of loading, or load cycles, which result in
cumulative damage. Bearing ensures that, as the shaft rotates, the mass carrier always
hangs vertically downwards. It should be clear that the force due to the mass carrier is f =
mg. this force applies a bending moment to the right-hand section of the shaft and the
bending moment due to F reaches a maximum at Shaft Bearing. Consider a point A at the
top of the shaft. Since the force F is tending to bend the shaft downwards, the shaft
material at A must be in tension. Similarly, the shaft material at a point B at the bottom of
the shaft must be loaded in compression. Now let the shaft rotate through 180o
so that point
A moves to the bottom and B to the top. The shaft material at A is now in compression
and the material at B is in tension. After a further shaft rotation of 180o
, A is again at the
top and in tension, while B is again at the bottom and is in compression. The total of
360o
of shaft rotation results in one complete load cycle for points A and B and, indeed, for
all points on the shaft. Figure shows a graph of the load cycles for points A and B.
Figure 2.7: Fatigue cracking phenomenon

2.7.2 Fatigue crack propagation
Within certain limits, the application of large numbers of load cycles may cause tiny
cracks to occur at highly stressed sections of the component. Subsequent load cycles cause
this microscopic crack to increase in size, slowly at first, but with increasing rapidity. If
not detected or checked in some way, the crack will eventually become so large, and will
so weaken the component, that it will fracture completely. The final failure may be sudden
and may have catastrophic consequences; nevertheless, fatigue cracking is a progressive
failurewhich has been occurring for some time prior to the final failure. Due to the
insidious nature of fatigue cracking and its potential to cause catastrophic failure,
designers need always to be on guard against design features which may lead to fatigue
failure. Items such as shafts which may undergo a very large number of rotations during
their lifetime always need to be designed with fatigue failure in mind.
2.7.3 Stress concentrations
It is observed in practice that fatigue cracks frequently occur where there is a sharp or
abrupt change in the shape of the component. Theoretical analysis and experimental
techniques both show that stresses within the material rise sharply at abrupt changes of
section. Such features are referred to as stress concentrations or stress raisers. Referring
again to above figure, it is seen that there is an abrupt change of shaft diameter close to
Bearing 2. This change in diameter is described as a shoulder on the shaft. Such a shoulder
causes a significant stress concentration. The location of the shoulder is already in a region
of high bending moment and therefore of high tensile and compressive stresses. The
combination of the two factors makes that cross-section of the shaft particularly vulnerable
to fatigue failure. Note that in above figure, the maximum bending moment on the shaft
actually occurs at Bearing 2, but the smaller shaft diameter and stress concentration due to
the shoulder makes this the cross section at which fatigue failure will occur. Changes of
cross-section other than shoulders which cause stress concentration effects in shafts
include:
• Keyways • Splines
• Circlip grooves • Threads
• Oil holes • Undercuts

2.8 Design Principles
The role of joints and drive shafts is to transmit torques between shafts which are not in
line. These transmitted loads are limited by the capacity of the materials used. Hence in
assessing the capacity of the joints it is most important to determine the pressure between
the rolling bodies and their tracks. It must however be decided whether short or long term
loading is involved:
– For short term loading the stress state is quasi-static. The joint is then designed so that
excessive plastic deformation does not occur,
– For long term loading the stress state is dynamic. The joint must be designed for many
millions of stress cycles.
The durability can only be determined by extensive rig tests, pure mathematical
approaches are still inadequate. Only in the case of Hooke’s joints is it possible to
calculate the life using modified methods from roller bearing practice and the empirical
Fischer equation. This cannot as yet be used for ball and pod joints. Joint manufacturers
use formulae based on the empirical Palmgren Eq. (2.1) to convert the durability from rig
tests into that corresponding to other torque, speed and angle conditions. When designing
machinery the designer does not know from the outset all the parameters, so he or she has
to draw up the design from basic data, some of which are estimated. The designer then
reassesses the joints with exact values for the static and dynamic stresses and can select a
joint from manufacturers’ catalogues: At this stage, all other factors such as the maximum
articulation angle, plunge and installation possibilities must be taken into account.
If one considers P1 = C as a reference load at which, with a constant speed, a rolling pair
achieves the life L1 = 106
, the indices can be omitted and the equation written as
L = 106
(C/P)p
. (2.1)
Figure 2.8: life vs. failed bearing numbers

2.9 Hooke’s Joints and Hooke’s Jointed Drive shafts
The torque capacity of joints is determined by the position of the rolling surfaces with
respect to the axis of rotation z. In the case of the Hooke’s joint the load P acts at a
pressure angle a = 90° to the y-axis and at a skew angle g = 0° to the axis of rotation z
(Figure 2.9). This is because the line of action p is perpendicular to z.Each transmitting
element comprises a number of rolling bodies.
2.10 Universal joint designs:
Cardan joints for industrial applications consist of variations using a cross and bearing
design. All designs (except for plain or composite bearing types) transmit torque through
anti friction bearings; two forged or cast yokes and a forged cross member. Heavy-duty lip
seals that are subject to eccentric loading prevent lubricant leakage and contamination.
This allows operation in contaminated atmospheres such as caster applications. Since
crowned rollers are typically used, the U-joint life can be statistically determined.
Hardened precision tolerance raceways are used with the bearing-steel rollers for optimum
life.
Figure 2.9: Position of the contact faces relative to the axis of rotation at the trunion,
a. side view, b. plan view

Mill universal joints can be categorized as one of the following five types:
• Closed eye (1-piece) yoke design (Figure 2.10) – A 1-piece yoke surrounds the bearing
housing.
• Split yoke design (Figure 2.11) – Yokes are split axially to produce a 1-piece bearing
housing with a solid bearing end cap whose yoke halves are held together with a tie
bolt during assembly, shipping and installation. After mill assembly, the halves are
held together by the bolted connection to the drive shaft flange.
• Split bearing eye (Figure 2.12) – Bearing bores are split into two sections and retained
by a combination of serrations and bolts.
• Block type (Figure 2.13) - Bearing housings are bolted to yokes with face keys, 1-
piece bearing housing bore.
• Composite plain bearing – Only design without roller bearings. Bearings are generally
made of a nonferrous material such as self-lubricating composite (used on low speed,
highly contaminated, high temperature applications such as steel continuous slab
casting machines.
The 1-piece yokes have the advantage of no maintenance requirement to verify if bolted
connections have loosened and elimination of precision matching of components for equal
Figure 2.11: split yokeFigure 2.10: Closed eye 1 piece yoke
Figure 2.13: block typeFigure 2.12: split bearing eye.

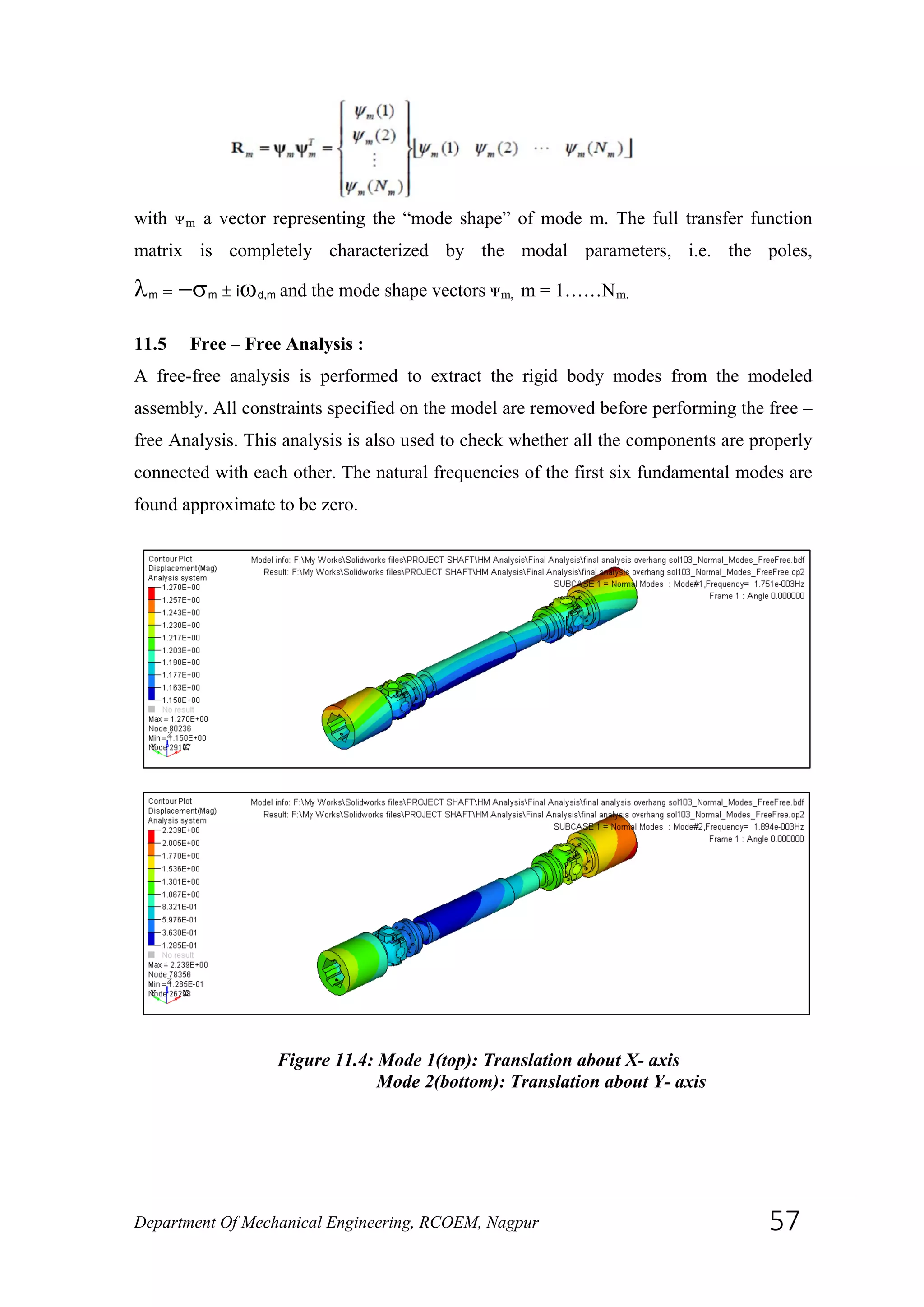
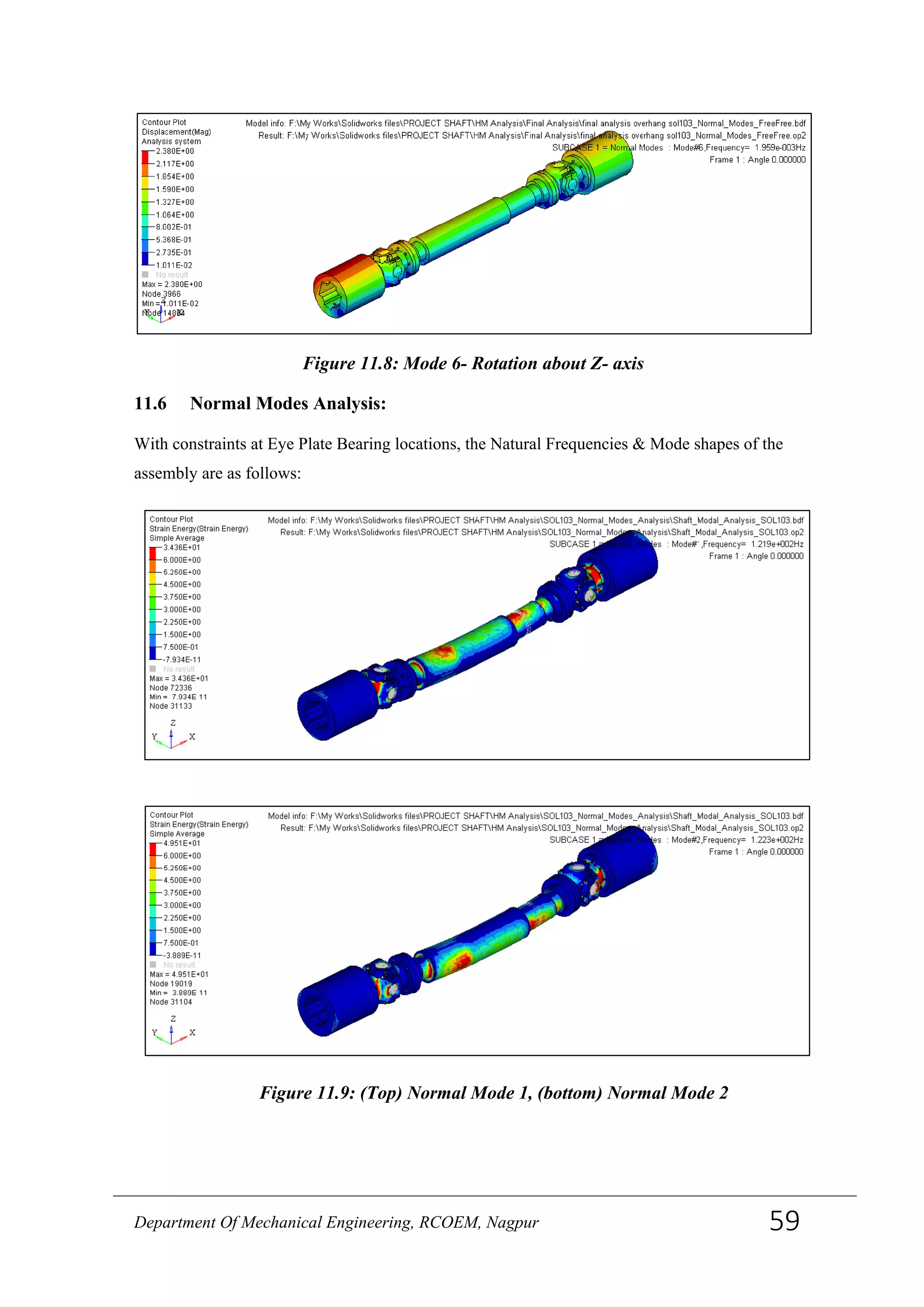
bearing loading. Corrosion issues associated with split bearing eye designs are also
avoided. The 2-piece yokes and block type designs were developed to increase the cross
trunnion diameter and torque capacity of the U-joint while allowing for assembly. Split –
yoke designs are unique since the tie bolt is not used for torque transmission or retention
of yoke components after installation. All designs have the option of splined centre
sections to allow for length compensation for axial travel and alignment changes during
operation. Splines can be hardened, typically by nitriding, for applications with frequent
axial travel. The centre sections can be tubes welded directly to the yokes or flanged to
allow for more economical replacement sparing of U-joint parts. It is uncommon to
machine integral face pads or special spline teeth between the flange faces (Fig.9 and 10)
on high load applications. [19]
2.11 General Considerations in shaft design.
2.11.1 To minimize both deflections and stresses, the shaft length should be kept as short
as possible and overhangs minimized.
1.11.2. A cantilever beam will have a larger deflection than a simply supported (straddle
mounted) one for the same length, load, and cross section, so straddle mounting should be
used unless a cantilever shaft is dictated by design constraints.
1.11.3. A hollow shaft has a better stiffness/mass ratio (specific stiffness) and higher
natural frequencies than a comparably stiff or strong solid shaft, but will be more
expensive and larger in diameter.
Figure 2.15: Radial face spline.Figure 2.14: Integral face pads

2.11.4. Try to locate stress-raisers away from regions of large bending moment if possible
and minimize their effects with generous radii and relief.
2.11.5. General Low carbon steel is just as good as higher strength steels (since deflection
is typical the design limiting issue).
2.11.6. Deflections at gears carried on the shaft should not exceed about 0.005 inches and
the relative slope between the gears axes should be less than about 0.03 degrees.
2.11.7. If plain (sleeve) bearings are to be used, the shaft deflection across the bearing
length should be less than the oil-film thickness in the bearing.
2.11.8. If non-self-aligning rolling element bearings are used, the shaft’s slope at the
bearings should be kept to less than about 0.04 degrees.
2.11.9. If axial thrust loads are present, they should be taken to ground through a single
thrust bearing per load direction. Do not split axial loads between thrust bearings as
thermal expansion of the shaft can overload the bearings.
2.11.10. The first natural frequency of the shaft should be at least three times the highest
forcing frequency expected in service, and preferably much more. (A factor of ten times or
more is preferred, but this is often difficult to achieve).
2.12 Design considerations for shaft
For the design of shaft following two methods are adopted,
• Design based on Strength: In this method, design is carried out so that stress at
any location of the shaft should not exceed the material yield stress. However, no
consideration for shaft deflection and shaft twist is included.
• Design based on Stiffness: Basic idea of design in such case depends on the
allowable deflection and twist of the shaft.
The stress at any point on the shaft depends on the nature of load acting on it.
The stresses which may be present are as follows.
 Basic stress equations:
𝜎 𝑏=
32𝑀
𝜋𝑑0
3(1−𝑘4)
Where,
M: Bending moment at the point of interest
do: Outer diameter of the shaft
k: Ratio of inner to outer diameters of the shaft ( k = 0 for a solid shaft because inner
diameter is zero )

 Axial Stress
𝜎 𝑎 =
4𝛼𝐹
𝜋𝑑 𝑜
3
(1 − 𝑘2)
Where,
F: Axial force (tensile or compressive)
α: Column-action factor (= 1.0 for tensile load)
The term α has been introduced in the equation. This is known as column action factor.
Column action factor arises due the phenomenon of buckling of long slender members
which are acted upon by axial compressive loads.
Here, α is defined as,
𝛼 =
1
1 − 0.0044𝐿/𝐾
𝑓𝑜𝑟
𝐿
𝐾
< 115 , 𝛼 =
𝜎 𝑦𝑐
𝜋2 𝑛𝐸
(
𝐿
𝐾
)2
𝑓𝑜𝑟
𝐿
𝐾
< 115
Where,
n = 1.0 for hinged end
n = 2.25 for fixed end
n = 1.6 for ends partly restrained, as in bearing
K = least radius of gyration, L = shaft length
σyc = yield stress in compression
 Stress due to torsion
𝜏 𝑥𝑦 =
16𝑇
𝜋 𝑑 𝑜
3
(1 − 𝑘4)
Where,
T: Torque on the shaft
τxy: Shear stress due to torsion
Combined Bending and Axial stress
Both bending and axial stresses are normal stresses; hence the net normal stress is given
by, next equation. The net normal stress can be either positive or negative. Normally,
shear stress due to torsion is only considered in a shaft and shear stress due to load on the
shaft is neglected.
 Maximum shear stress theory
𝜎 𝑏=
32𝑀
𝜋𝑑0
3(1−𝑘4)
+
4𝛼𝐹
𝜋𝑑 𝑜
3(1−𝑘2)

Design of the shaft mostly uses maximum shear stress theory. It states that a machine
member fails when the maximum shear stress at a point exceeds the maximum allowable
shear stress for the shaft material. Therefore,
𝜏 𝑚𝑎𝑥 = 𝜏 𝑎𝑙𝑙𝑜𝑤𝑎𝑏𝑙𝑒 = �(
𝜎𝑥
2
)2 + 𝜏 𝑥𝑦
2
Substituting the values of σx and τxy in the above equation, the final form is, therefore,
𝜏 𝑎𝑙𝑙𝑜𝑤𝑎𝑏𝑙𝑒 =
16
𝜋𝑑 𝑜
3
(1 − 𝑘4)
��𝑀 +
𝛼𝐹𝑑 𝑜(1 + 𝑘2)
8
�
2
+ 𝑇2
the shaft diameter can be calculated in terms of external loads and material properties.
However, the above equation is further standardised for steel shafting in terms of
allowable design stress and load factors in ASME design code for shaft.
 ASME design Code
The shafts are normally acted upon by gradual and sudden loads. Hence, the equation is
modified in ASME code by suitable load factors,
𝜏 𝑎𝑙𝑙𝑜𝑤𝑎𝑏𝑙𝑒 =
16
𝜋𝑑 𝑜
3
(1 − 𝑘4)
��𝐶 𝑏𝑚 𝑀 +
𝛼𝐹𝑑 𝑜(1 + 𝑘2)
8
�
2
+ (𝐶𝑡 𝑇)2
2.13 Joint Selection (Torque Rating)
The capacity of a universal joint is the torque which the joint can transmit. For a given
joint, this is a function of speed, operating angle and service conditions. Section 2.13.1
shows use factors based on speed and operating angle for two service conditions:
intermittent operation (say, operational or less than 15 minutes, usually governed by
necessity for heat dissipation) and continuous operation. The torque capacity of a single
Cardan joint of standard steel construction is determined as follows:
From the required speed in RPM, operating angle in degrees, and service condition
(intermittent or continuous), find the corresponding use factor from Table.
Multiply the required torque, which is to be transmitted by the input shaft, by the use
factor. If the application involves a significant amount of shock loading, multiply by an
additional dynamic factor of 2. The result must be less than the static breaking torque of
the joint.

2.13.1Factors for the Torque Rating of Universal Joints [23]
2.14 Selection criteria
2.14.1 Torque requirements:
The first step in selecting a Cardan shaft is determining the maximum torque to be
transmitted. The maximum torque should take into account the maximum prime mover
torque including inertial effects from the prime mover when decelerating during
overloads. The prime mover torque is generally considered as being unequally split
through the pinion stand in the range of 40 to 67% to allow for unequal torque loading of
the mill rolls.
This application torque is adjusted by applying the appropriate service factor(s) in
accordance with the joint manufacturer’s recommendation. The resultant selection torque
is compared to either: the U-joint’s endurance or fatigue torque rating for reversing
applications; or the one Way or pulsating fatigue torque rating for non-reversing
applications. Both the ratings are based on the material strength of shaft. The one way
torque rating is typically 1.5 times the reversing fatigue torque rating.
2.14.2 Maximum bending moment
During joint operation bending moment occur in the connecting shaft as function of
operating misalignment angle and driving torque. This bending moment causes a load on
supporting bearing that is periodic with two complete cycles per revolution of shaft. The
bending moment is always in plane of the ears of the yoke. The maximum value of
bending moment is given by
M = T tan (α)
Where, M = maximum bending moment

T = operating torque
α = operating angle
2.14.3 Axial travel requirements and axial forces
Gear spindles are designed to accommodate angular misalignment and small changes in
axial travel length by having their hubs transverse within or pull out in sleeves. However
U joints are required to have a clearance fit in connected equipment or a spline travel
section in intermediate shaft. A clearance or slip fit allows roll end to slip out or pull-out
under misalignment. The amount of pull-out is calculated from:
Pull out = CL (1- cosα)
CL = centreline to centreline of joint flex location
α = operating miss alignment angle
Axial travel of u joint spline under torque results in axial force being applied to support
bearing these forces are function of spline coefficient of friction operating torque
operating angle and spline pitch diameter axial force can be calculated by
𝐹𝑎𝑥𝑖𝑎𝑙 =
2𝑇𝜇𝑐𝑜𝑠𝛼
𝑃𝑑
Where,
T = operating torque
U = coefficient of friction
α = operating angle
Pd = spline pitch diameter
The same equation is used for gear spindle force with a length compensating spline. For
spindles without length compensating splines the same equation is used expect that Pd is
equal to crowned gearing is used. The larger pitch diameter would reduce the axial forces
proportionately

2.15 Special consideration
2.15.1 Applicability
Universal joints are particularly well suited for the angularity requirements of reversing
rougher mill applications. The rolls of these mills are usually powered by two separate
direct drive motors that are speed synchronized by the mill control system. The mills are
required to operate through a relatively large range of angularity. A range from 5° to 2°
during a single schedule is common. Angularity in excess of 6° is not recommended in
these applications.
Due to motor overload capabilities built into these mills and the low minimum speed of
motors, it is more appropriate to consider the torque density of the application rather than
the power density. Motors for this application normally have a current limit setting
between 220and 250% of the nameplate motor rating. When the overload factors and
minimum motor speeds are taken into account, the designer can be faced with an 8000 or
10000-hp mill motor that can produce 1.5 million ft-lb of torque at current limit and is
capable of generating torque spikes in excess of 2.0 million ft-lb. This torque must
transmitted through a universal joint spindle is well suited for these application.
Compared to finishing stand application these types of mills run relatively slowly. The
faster steckel mills rarely- exceed 120 or 140 rpm accordingly, dynamic balancing of
spindle component is not normally required.
2.14.2 Size selection
Size selection for reversing roughers mills requires careful consideration of all operating
conditions. Because of the overload capabilities, using catalogue torque ratings are usually
not useful and can be misleading. The two main factors that usually determine the final U-
joint sizing are minimum work roll diameter; and who is specifying the U-joint.
To obtain the maximum possible reduction per pass, mill designers (particularly on steckel
mills) specify the work rolls as small in diameter as possible. The question of how to get
the required torque to the work rolls is usually a secondary consideration. As a result, the
discard diameter of work rolls is, in many cases, the deciding factor when choosing the
size of universal joints, at least for the roll end U-joint. Often the spindle designer finds

that universal joints, that is, for example, 900 mm dia. may be required to meet the desired
overload criteria. However, the discard size of the work rolls for the mill is 850 mm. The
swing diameter of the roll end joint must be equal to less than 850mm. this does not
adversely affect the functionality of mill. It only means that the service life of the
universal joint bearing will be shortened.

CHAPTER 03 PROBLEM IDENTIFICATION AND APPROACH
3.1 Sunflag: Details about BSM
A detailed study of the process at Sunflag Iron and steel limited, Bhandara was carried out.
The department of main focus was the Bar and Section Mill. The department is equipped
with the 60 tonnes per hour, 20 stand, 2 high continuous Mannesmann designed rolling
mill, duel fuel walking hearth type re-heating furnace, process control through ABB
automation, Online gauging system, Closed circuit TV system for billet and bar
movements.
3.2 Problems Identified
Rolling mill stands are driven by electric motor, capacity depending on the stand number.
The various problems associated with the rolling mill setup are excessive shock, bearing
failure, shaft failure, etc. The universal joint shaft is the main concern of this project.
The failure prone areas of the shaft are the needle bearings of the universal joint cross or
the spider and the yoke pin or the locating pin failure. The spider has needle bearings,
which fail nearly every 3 months, damaging the yoke pin. The yoke pin also faces severe
stresses in crushing, bending and wears out frequently.
3.3 Actual Problem
The billet has a larger cross section area at the entry to a stand. It strikes the roller, causing
a jerk. Also, the billets have some small air pockets trapped inside them. When the billets
pass in between the rollers, these air pockets are compressed and its temperature increases
simultaneously. As a result, they explode, in small proportions. This causes a reaction
force on the rollers, normal to its axis. Some of the jerk produced due to this is transmitted
along through the wobbler to the yoke pin. This causes the yoke pin to wear out the area
between its surface and that of the eye plate. This increases the clearance between their
surfaces and eventually, the shaft begins to wobble more. This in turn causes the bearing
to fail in crushing. With no relative motion between the components in the universal joint,
the assembly finally gets jammed.
3.4 Approach
The approach followed during the project is as follows:
 Study of rolling process at Bar and section mill at SUNFLAG IRON AND STEEL,
Bhandara.

 Study of various failures occurring in the shaft.
 Understanding the causes of the failure and the ways of repairing the shafts.
 Acquiring the standard drawings, and other information like material of shaft, failure
frequency, etc.
 Calculation of the forces and torque required for rolling process.
 Calculating the design torque for shaft design.
 Modelling the shaft in SolidWorks 2013.
 Pre-processing the Shaft in HyperMesh11.0.0.39
 Solving in Nastran.
 Postprocessing in HyperView.
 Obtaining the results like
o Deflection,
o Stresses induced at various sections,
o The critical sections,
o Reactions at the bearings,
 Suggesting modifications in the design to reduce the failures and increase the time
between the repairs.

CHAPTER 04 PROCESS AT BSM, SUNFLAG STEEL,
BHANDARA
• Rolling is done in 5 stages through Variable Reduction Process:
o 1-4 - Roughing Mill
o 5-8 - Roughing Mill
o 9-14 – Intermediate Mill
o 15, 17, 19 – Finishing Mill
o 16, 18, 20 – Vertical Stand
• Total 23 rolling machines arranged in a line for reduction of billet size (130 x 130mm
sq.) from roughing up to finishing (Ø5.5mm) stage.
The different types of mills used in the steel plant are described below:
4.1 Roughing Mills:
• There are four pairs of shafts i.e. 8 shafts used to provide power to the roughing mills.
The shafts are numbered from 1 to 8 and are divided into two sections. One consists of
shafts from 1 to 4 and other from 5 to 8.
• Roughing mills quickly remove large amounts of material. This kind of mill utilizes a
wavy tooth form cut on the periphery. These wavy teeth form many successive cutting
edges producing many small chips, resulting in a relatively rough surface finish.
During cutting, multiple teeth are in contact with the work piece reducing chatter and
vibration. Rapid stock removal with heavy milling cuts is sometimes called hogging.
Roughing mills are also sometimes known as ripping cutters.
• Greater reduction in diameter occurs in this mill hence the stresses and forces on the
transmission shaft are the highest here.
4.2 Intermediate Mills:
• There are six shafts used to transmit power to the intermediate rolling mills. The shafts
are numbered from 9 to 14.
• The thickness of the billet is reduced further but not by the same margin as in roughing
mills. The thickness after coming out from the mills is close to the required value.
• The shaft associated with this mill has been chosen to study and analyze in our project.

4.3 Finishing Mills:
• There are three shafts used to transmit the power to the finishing mill. The shafts are
numbered 15, 17 and 19 respectively.
• In this type of mill the billet is finished to the required size and shape.
• By now, the steel has been rolled into a flat bar as long as 200 feet. In contrast to the
roughing mills, the finishing mills roll the transfer bar in tandem, meaning each bar
will be rolled through all six stands at once. The hot steel is quite fragile as it is rolled
and tension between the finishing mill stands must be closely controlled at very low
levels in order to avoid stretching or tearing the strip.
• Prior to the finish rolling operation, the head- and tail-ends of the transfer bar will be
sheared to square them up, helping to ensure proper threading and tail-out. A final
two-stage descaling operation is performed to clean off the scale that has grown on the
bar during roughing.
• It is important to smoothly adjust the roll gaps and speeds to maintain stable rolling of
strip to the necessary thickness in spite of the temperature variations present in every
bar.
4.4 Vertical Stand
• A vertical rolling mill stand is a combination of horizontal and vertical mill stand that
is used where material running speed is very high and also we can roll the material
without using twist pipe.
• To reduce the slabs up to 150 mm in width and to form the workpiece edges, this
vertical rolling mill stand is fitted with the rolls with grooves and hydraulic screw-
down mechanisms.
• It has heavy duty construction, a sturdy design, requires low maintenance, has easy
operation and is dimensionally accurate.

CHAPTER 05 ROLLING MACHINE
Parts of a rolling Machine
1. Roller Guides with roller bearings
2. Transmission Shafts
3. Universal couplings with wobblers
4. Gear Box
5. Flange
6. Motor
7. Rollers
1. Roller Guides with roller bearings:
Roller guides are the guides used to make sure that the rollers rotate in the proper direction
and with less friction between the rollers and the bearings. Roller bearings are the bearings
which support the rollers as they rotate. The rollers should be able to withstand huge
forces and hence the guides and bearings play an important role.
2. Transmission Shafts:
It is a mechanical component for transmitting torque and rotation, usually used to connect
other components of a drive train that cannot be connected directly because of distance or
the need to allow for relative movement between them. Transmission shafts are carriers
of torque: they are subject to torsion and shear stress, equivalent to the difference between
the input torque and the load. They must therefore be strong enough to bear the stress,
whilst avoiding too much additional weight as that would in turn increase their inertia. To
allow for variations in the alignment and distance between the driving and driven
components, transmission shafts frequently incorporate one or more universal joints, jaw
couplings, or rag joints and sometimes a splined joint or prismatic joint.
Figure5.2: Parts of Rolling Mill.Figure 5.1: Shaft and roller setup

3. Universal couplings with wobblers:
Coupling in a rigid rod that allows the rod to 'bend' in any direction, and is commonly
used in shafts that transmit rotary motion. It consists of a pair of hinges located close
together, oriented at 90° to each other, connected by a cross shaft. Wobblers prevent
wobbling of the shaft that is unsteady motion from side to side. This makes sure that shaft
is rotation properly and hence transmitting power to the rolling mills.
4. Gear box:
A gearbox is a mechanical device utilized to increase the output torque or change the
speed (RPM) of a motor. The motor's shaft is attached to one end of the gearbox and
through the internal configuration of gears of a gearbox, provides a given output torque
and speed determined by the gear ratio.
5. Flange:
A rib or rim for strength, for guiding, or for attachment to another object. It is located after
the gearbox but before the motor. It makes sure that the motor and the gearbox are
properly attached as this is an important factor for power transmission between the motor
and the shaft.
6. Motor:
It provides the power for the complete rolling process. It converts the generated electric
power into mechanical power and transmits it to the shaft through the gearbox at the
required torque and RPM.
7. Rollers:
Rollers are the most important part of a rolling machine. These bear the shocks of the
billet and compress the work piece to a new cross section.

CHAPTER 06 BASIC CALCULATIONS AND ASSUMPTIONS
6.1 Data obtained from Sunflag Iron and Steel plant (actual run time data)
Table 6.1: Velocity, rpm and reduction data.
Stand Velocity(m/s) Ref. rpm Actual rpm Reduction
9 1.32 720 719 1.35
10 1.72 647 647 1.31
11 2.25 731 733 1.31
12 2.88 738 739 1.28
The above data is obtained for final section RND 26 (i.e. Round with diameter= 26mm)
The cut length of billet is = 6.652 m
Expected finished length = 400 m
Billet (raw material) grade = SAE 1020
a. Shaft data:
Material: EN 24 i.e. SAE 4340 Motor rpm: 720 rpm
Gear ratio: 9.109 Shaft rpm =
720
9.109
= 79.04 𝑟𝑝𝑚
b. Roll data:
Roll diameter Do = 360.5 mm Roll groove height = 12.72 mm
Roll radius outer = 180.25 mm Roll inner radius = 167.53 mm
Gap between rolls = 11.5 mm
c. Temperature data:
Temperature of billet at the exit of furnace = 1200 ºC
Temperature of the billet at stands no. 9 = 950-1000 ºC
Ambient temperature of surrounding = 30-40 ºC

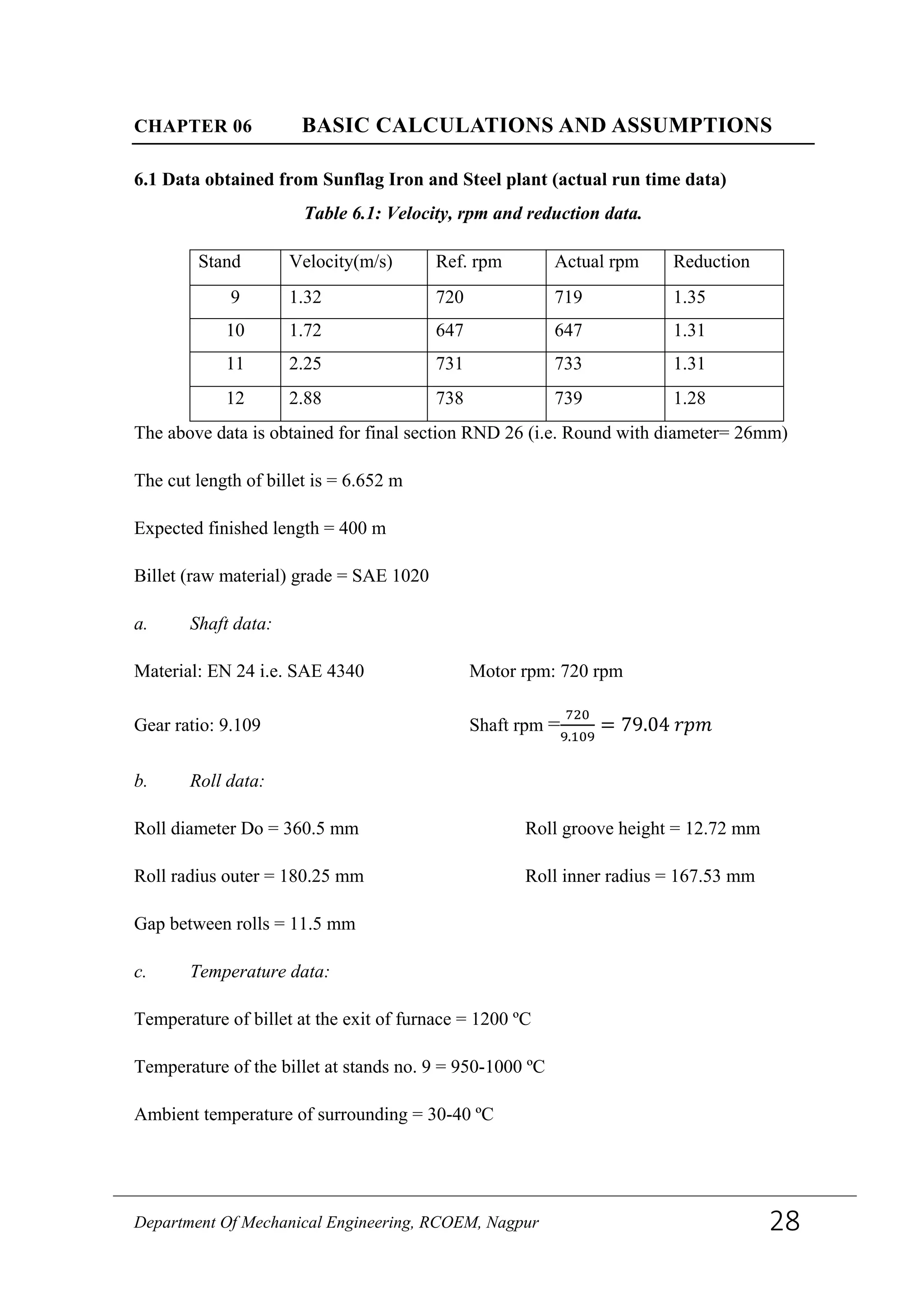
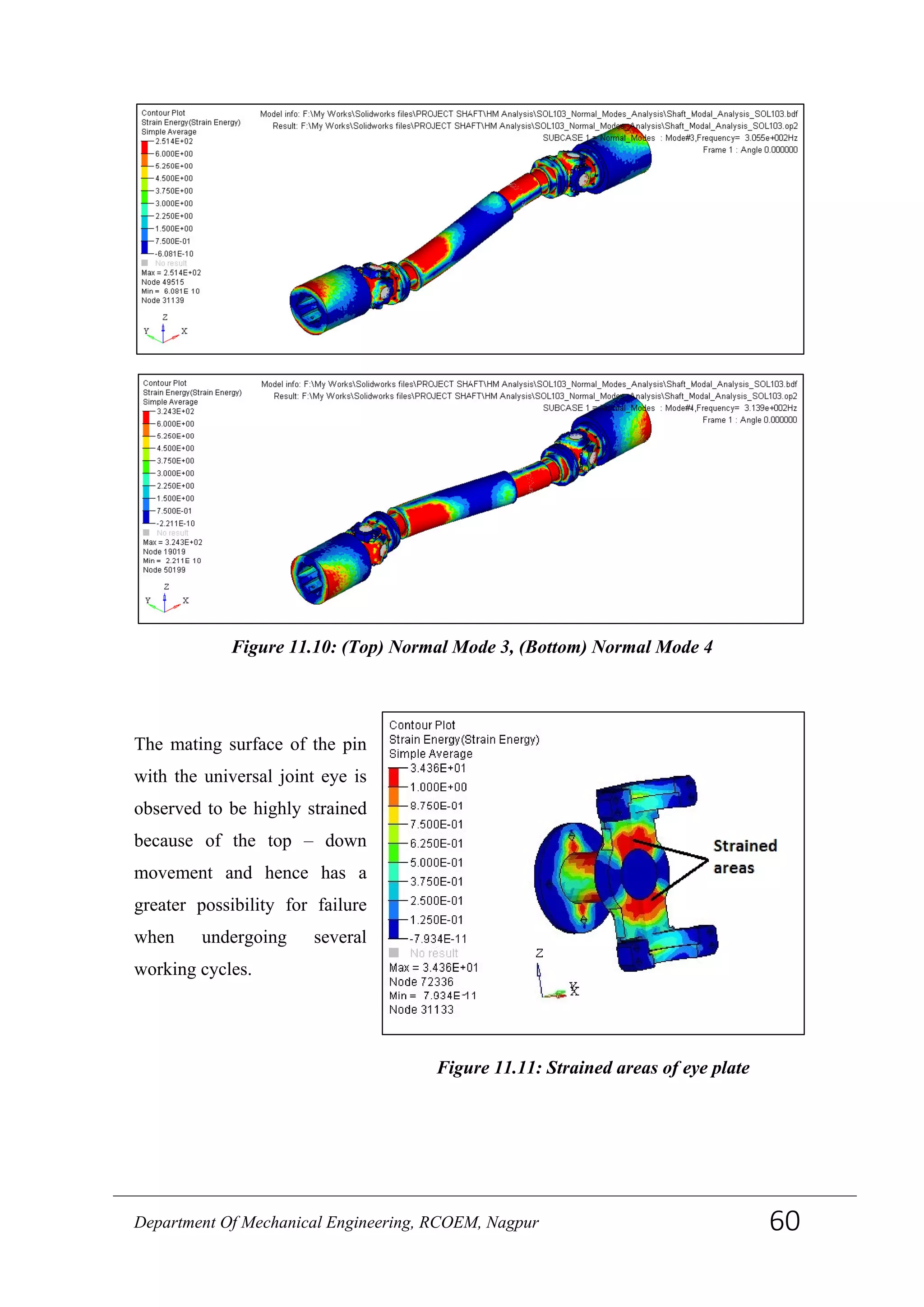
6.2 Basic assumption
The rolling setup considered for this project is a bar mill for hot rolling of steels. To create
a closed form expression for the roll torque in rod rolling is very difficult. The governing
differential equation is much more complicated than in flat rolling since the stress state no
longer can be regarded as two dimensional. The geometry of the roll pass is more complex
to describe and all the other aspects such as describing the amount of inhomogeneous
deformation, interfacial friction etc. is also present in rod rolling. The traditional approach
is to relate the round or oval bar into an equivalent square section and then use some
analytic expression for flat rolling. Since the expressions for the roll torque in flat rolling
are not very accurate, one cannot expect these expressions combined with equivalent
rectangle methods to perform well. Another approach to try to adopt the flat rolling
expressions into rod rolling was introduced by Y. Lee and Y.H. Kim. In their study of the
roll force they introduce the weak plane-strain concept in order to produce a closed form
expression for the roll force. Since the strain in lateral direction in rod rolling is
constrained by the groove radius Lee and Kim argues that the stress state can be regarded
to be in a weak plane condition. They introduce a simple linear function to compensate for
the three-dimensional stress state in the roll gap in rod rolling. The pressure in rod rolling
is then presented as:
𝒑 𝒓𝒐𝒅 = (𝟏 − 𝜺 𝟏)𝒑 𝒑𝒍𝒂𝒏𝒆 𝒔𝒕𝒓𝒂𝒊𝒏
Where, ε1 is the lateral strain. An equivalent rectangle method is used to calculate average
effective strain and strain rate. They conduct an evaluation of their expression to measured
values from one round to oval and one oval to round pass at different temperatures. The
average difference between measured and calculated roll force in the three different
temperature levels was between 0.8-5.7 percent, where the calculated values overestimates
the roll force. Since the experiments were conducted in one round to oval pass and one
oval to round pass, no conclusions about the consistency of the model when the geometry
data of the roll pass is varied can be made. They do not consider the calculation of the roll
torque, and therefore it is only noted here that the weak plane strain concept might be a
fruitful way to find a consistent model for the roll torque in round oval sequences. This
method is based on the use of statistical design and modeling of results from FEM-
simulations. [22]
Equivalent rectangle is rectangle with same area as that of the circle but the cross section
is square instead of originalcircular section.

6.3 Calculation of area of cross section at the inlet and outlet to stand no 9:
Initial cross section area of the billet = 160 × 160 𝑚𝑚2
= 25600 𝑚𝑚2
Length of billet = 8 meters
Final round section diameter = 26 mm
Area = =
𝜋𝑑2
4
= 530.93 𝑚𝑚2
For calculating the final length we have equation
A1L1 =A2L2
25300 X 8000 = 530.93 X L2
L2 = 385.74 m
At the first pass, the area of cross section remains the same since reduction factor is 1.00
(reduction factor = 1.00 means zero reduction in the area). The cross section changes from
square (initial billet cross section) to oval.
Therefore area of cross section of the round billet after pass no 1 = 25600mm2
At pass 2 the reduction factor is 1.3 which means a 30 % reduction in the area
Therefore area of billet at exit of pass no. 2
= 1 −
30
100
× 25600
= 17920mm2

Thus the area of cross section after each pass is shown in the following table:
Table 6.2: Areas of the billet at inlet and exit of pass.
Side of billet = 160 mm
standno.
Rfactor
Areaatinlet
Areaatexit
1.00 1.000 25600.00 25600.00
2.00 1.300 25600.00 17920.00
3.00 1.290 17920.00 12723.20
4.00 1.270 12723.20 9287.94
5.00 1.280 9287.94 6687.31
6.00 1.210 6687.31 5282.98
7.00 1.270 5282.98 3856.57
8.00 1.280 3856.57 2776.73
9.00 1.350 2776.73 1804.88
10.00 1.310 1804.88 1245.36
11.00 1.310 1245.36 859.30
12.00 1.280 859.30 618.70
13.00 1.000 618.70 618.70
14.00 1.000 618.70 618.70
(Highlighted rows indicate that the passes are shutoff due to process requirement)
In the above calculations, billet cross section area at the exit of one pass is assumed to be
equal to the area of billet cross section at entry to the next pass (i.e. the effect of drawing is
neglected)
The billet is simultaneously in multiple stands in a rolling mill. The rollers pull the billet
with different forces. This causes a drawing effect in the billet. This area is reduced due to
the inter stand tension. Here for ease of calculation this effect is neglected. As the main
concern of analysis project is to consider the failure in the universal joint assembly of the
shaft the effect of inter stand tension which reduces the applied torque is neglected. It is of
main concern when the rollers or the bearing are to be analysed or designed

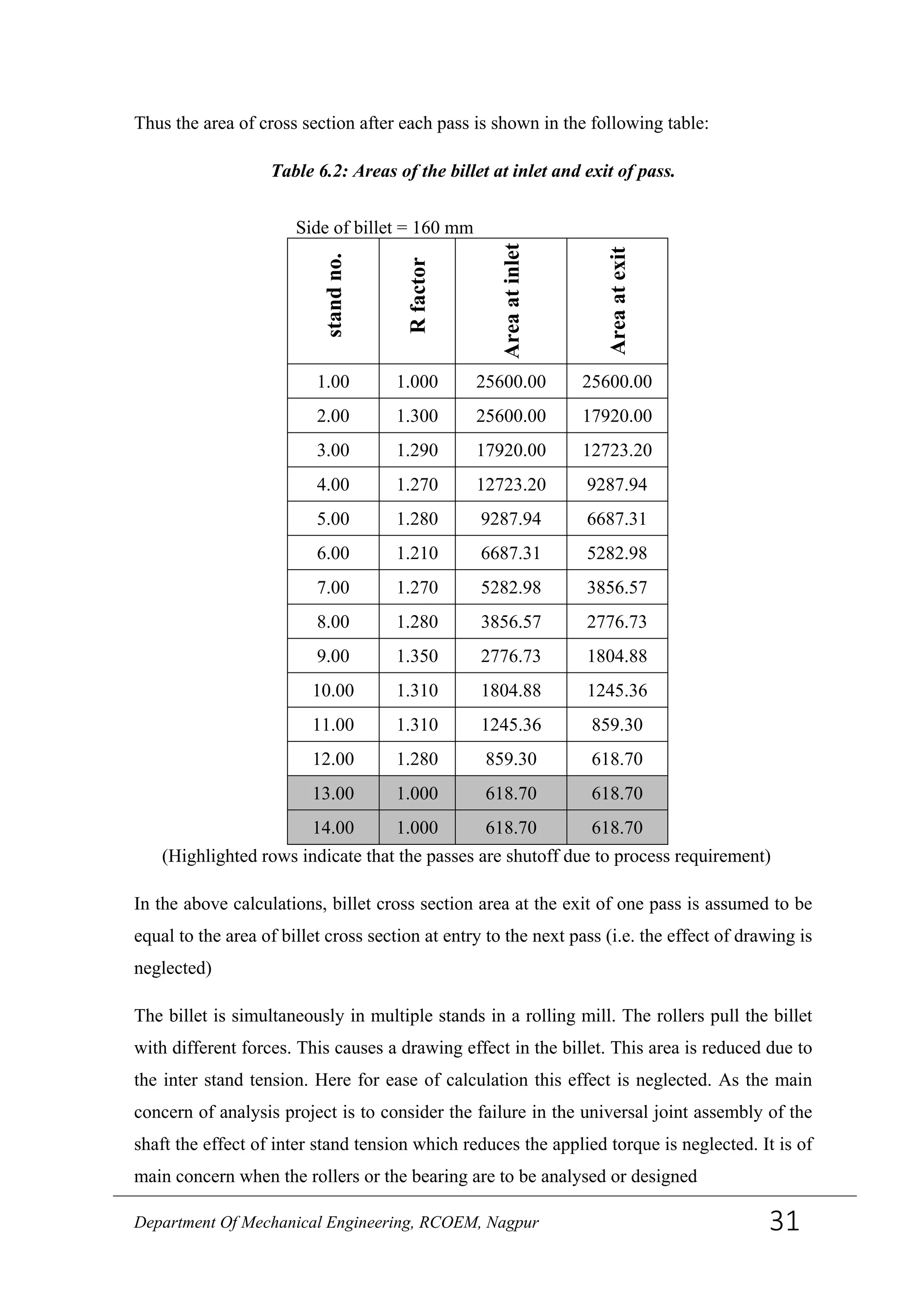
Thus the area of the billet at the entry to the stand no 9 i.e. A1 = 2776.73 mm2
The area of cross section at the exit of stand no 9 is A2 = 1804.88 mm2
As the billet passes through the stands its cross section after passing from each stand
differs from the shape with which it feeds into the rollers i.e. for a particular stand if the
exit cross section is circular for the next stand the inlet cross section becomes elliptical
which means that if the inlet section is circular the exit section should be elliptical and
vice versa. [10]
Thus the diameters of the billet at the inlet and exit section are calculated as follows
Diameter of billet at the inlet D1 =�2776.73 × 4 ×
1
𝜋
= 59.46 mm
Similarly, diameter at the exit: D2 = 47.94 mm (for perfectly circular shape)
But, since the section at exit is not completely circular and is elliptical due to roll
geometry,
1804.88 = 𝜋 × ℎR
2× Rw2
Where, h2 = 17.67 mm, which is found from the roll geometry and roll gap given
∴ 𝑤2 = 32.6 𝑚𝑚
Figure 6.1: incoming and outgoing section geometry of work piece at roll pass.(a):circle
to oval, (b): oval to circle

As per the above figure and according to our assumption the work piece height and width
(𝑖. 𝑒 2ℎ 𝑎𝑛𝑑 2𝑤) equal the diameter of the work piece Thus,
2𝑤1 = 2ℎ1 = 𝐷1 = 59.46𝑚𝑚
𝑤1 =
𝐷1
2
= 29.73 𝑚𝑚, 𝑎𝑛𝑑 ℎ1 =
𝐷1
2
= 29.73
ℎ2 = 17.67𝑚𝑚 𝑎𝑛𝑑 𝑤2 = 32.6𝑚𝑚 -----------from roll geometry and area of work piece.
Figure 6.2: Actual roller-billet geometry.

CHAPTER 07 ANALYSIS FOR CALCULATION OF ROLL
FORCE AND TORQUE
7.1 Contact length or the roll bite length:
It is the distance between the two points on the rolls, along the circumference at which the
work piece enters and leaves the rollers. In this case,
𝐿 𝑟 = �2𝑅𝑖(ℎ1−ℎ2)
𝑅𝑖 = Inner roll radius =
360.5−2∗12.72
2
= 167.53𝑚𝑚
By substituting 𝑅𝑖,ℎ𝑖 = 29.73𝑚𝑚 , ℎ2 = 32.6𝑚𝑚, 𝐿 𝑟= 63.56mm
For the equivalent rectangle assumption, the section height 2h at any distance x from the
entry is given by
ℎ = ℎ1 −
𝐿 𝑟
𝑅𝑖
𝑥 +
𝑥2
2𝑅𝑖
ℎ = 29.73 −
63.56
167.53
𝑥 +
𝑥2
2 ∗ 167.53
ℎ = 29.73 − 0.3974𝑥 + 2.984 × 10−3
𝑥2
(7.1)
The section maximum width 2𝑤 is approximated to have a parabolic distribution along
the roll bite length, given by
𝑤 = 𝑤1 − 2(𝑤1-𝑤2)
𝑥
𝐿 𝑟
+ (𝑤1 − 𝑤2)
𝑥2
𝐿 𝑟
2
𝑤 = 𝑤1 − 2(29.73 − 32.67)
𝑥
63.56
+
(29.73 − 32.67)
63.562
𝑥2
𝑤 = 29.73 − 0.0925𝑥 − 7.297 × 10−4
𝑥2
(7.2)
Equation 7.2 is formed such that it satisfies the boundary conditions 𝑤 = 𝑤1at 𝑥 = 0 and
𝑤 = 𝑤2 at 𝑥 = 𝑙 𝑟 𝑎𝑛𝑑
𝑑𝑤
𝑑𝑥
= 0 at 𝑥 = 𝑙 𝑟 which are the conditions taken by default
while analyzing or formulating the rolling process for sheet rolling. [10]
The projected area of work piece-roll contact surface on the x-z plane is approximated to a
semi elliptic shape of a width 2b at exit and 2b at any section at distance x from the entry
expressed as
𝑏 = 𝑏2�
2𝑥
𝐿 𝑟
−
𝑥2
𝐿 𝑟

𝑏 =
26.72
2
�
2𝑥
63.56
−
𝑥2
63.562
(7.3)
7.2 Calculation of effective roll radius
The effective roll radius is obtained from the maximum roll radius, 𝑅 𝑜 , roll gap G and
work piece exit maximum width 2𝑤2 and exit cross section area 𝐴2 as,
𝑅 𝑒 = 𝑅 𝑜 − 0.5 �
𝐴2
2𝑤2
− 𝐺� (7.4)
𝑅 𝑒 = 180.25 − 0.5 �
1804.88
2 ∗ 17.67
− 11.5�
𝑅 𝑒 = 164.125𝑚𝑚
The above equation 9.4 works only when the exit cross sectional shape is rectangular.
Equation 9.4 is based on equivalent rectangular approximation method that transfer the
non-rectangular cross section into rectilinear one of width equal to the maximum width of
the cross section while the net cross sectional area is maintained the same. [10]
7.3 Calculation of strain and strain rate
For homogeneous deformation of work piece in the direction of height and width, the
respective strain component can be found as follows.
The load deflection curve for ductile material is shown in the following figure.
Hot rolling involves plastic deflection of the work piece strain =
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑙𝑒𝑛𝑔𝑡ℎ
𝑜𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ
Figure 9.1: Stress strain relation for steels

𝑑𝜀 = −
𝑑𝑥
𝑥
=
𝑓𝑖𝑛𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ − 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ
𝑜𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑙𝑒𝑛𝑔𝑡ℎ
Integrating, with limit from 𝐿𝑖 𝑡𝑜𝐿 𝑜
𝟄 = � 𝑑𝟄 = �
𝑑𝑥
𝑥
𝐿0
𝐿 𝑖
= [ln 𝑥]
= − ln �
𝑙 𝑖
𝑙 𝑜
� (7.5)
Note: the ‘- ve ‘sign can be neglected for calculations as it indicates whether strain is due
to tension or compression.
Thus along the height of the work piece,
𝟄 𝑦 = ln �
ℎ
ℎ1
�
𝟄 𝑦 = ln
29.73
17.67
= 0.52
Similarly, strain along the width direction,
𝟄 𝑧 = ln �
𝑤1
𝑤2
�
𝟄 𝑧 =
17.6
29.73
= −0.0943
The volume of the work piece remains constant during the complete rolling process.
Thus,
𝟄 𝑥 + 𝟄 𝑦 + 𝟄 𝑧 = 0
𝟄 𝑥 = −�𝟄 𝑦 + 𝟄 𝑧�
𝟄 𝑥 = −(0.52 − 0.0943) = −0.4257
Neglecting the shear strain components, the effective strain obtained as

𝟄 𝑟��=�
2
3
�𝟄 𝑥
2 + 𝟄 𝑦
2 + 𝟄 𝑧
2� (7.6)
𝟄 𝑟�� = 0.5541
7.4 Calculation of effective strain rate
Strain rate or the effective strain rate is the rate of change of strain, and is given by
𝜀̅̇ =
𝜀
𝑡 𝑝
(7.7)
Where 𝜀 is the strain and 𝑡 𝑝 is the time required for a paint or the work piece to pass
through contact length. [11]
𝑡 𝑝 Can be calculated by the relation
𝑡 𝑝 =
60× 𝐿 𝑟
2𝜋𝑁 𝑅 𝑒𝑓𝑓
(7.8)
𝑡 𝑝 =
60 ∗ 63.56
2𝜋 ∗ 79 ∗ �
167.53+180.25
2
�
𝑡𝑝 = 0.047𝑠𝑒𝑐
Thus, the strain rates can be calculated by using equation (7.8) as,
𝜀̇ 𝑦 =
𝜀
𝑡 𝑝
=
0.52
0.047
= 11.108 s-1
𝜀̇𝑧 =
𝜀 𝑧
𝑡 𝑝
=
−0.0943
0.047
𝜀̇𝑧 = −2.014 s-1
Again, by law of conservation of volume,
𝜖 𝑥̇ =−�𝜖 𝑦̇ + 𝜖 𝑧̇ � (7.9)
𝜖 𝑥̇ = 0.094 s-1
Resultant strain rate,

𝜀 𝑟̇� = ��𝜖 𝑥̇ 2
+ 𝜖 𝑦̇ 2
+ 𝜖 𝑧̇ 2
� = 11.84 s-1
7.5 Calculating the material properties at rolling condition
From the above analysis and given data,
The temperature of a work piece at a stand is around 1000O
C.
Strain in the work piece along the height (y- direction) = 0.52
Strain rate in the work piece along the height (y- direction) = 11.108
For finding the flow stresses of a material at a given conditions of strain, strain rate
temperature, various equations can be used. Flow stress using Shida’s equations at a given
conditions can be found out.
Since, a rolling mill setup can be used for rolling of various types of steels, the calculation
of flow stresses for steels containing varying proportion of carbon and other constituents
are ( Properties mainly depend on the carbon content in the steel ) .
7.6 Shida’s equation for finding flow stresses
At a temperature of 1000O
C and carbon content of 0.2%,
𝜎 𝑝 = 𝜎𝑓 ∗ 𝑓𝑟 ∗ 𝑓 �
𝑘𝑔𝑓
𝑚𝑚2� (7.10)
𝑇 =
1000 + 273
1000
= 1.273
𝑇𝑝 = 0.95 ×
𝐶+0.41
𝐶+0.32
= 1.1144 (7.11)
For T ≥ 𝑇𝑝,
𝜎𝑡 = 0.28 ∗ 𝑒𝑥𝑝 �
5
𝑇
−
0.01
𝐶+0.05
� = 13.664 (7.12)
𝑚 = (−0.019𝐶 + 0.126)𝑇 + (0.075𝐶 − 0.05) = 0.12
𝑛 = 0.41 − 0.07𝐶 = 0.396
𝑓 = 1.3 × (5𝜀) 𝑛
− 1.5𝜀 = 1.118 (7.13)
𝑓𝑟 = (
𝜀̇
10
) 𝑚
= 1.013 (7.14)
Thus, 𝜎 𝑝 = 15.47
𝑘𝑔𝑓
𝑚𝑚2 = 151.76𝑀𝑃𝑎
For T < 𝑇𝑝, the equations to be followed are:

𝜎𝑡 = 0.28 ∗ 𝑞( 𝑐, 𝑡)exp �
𝑐 + 0.32
0.19 (𝑐 + 0.41)
−
0.01
𝑐 + 0.05
�
𝑞(𝑐, 𝑡) = 30(𝑐 + 0.9)(𝑇 − 0.95 ∗
𝑐 + 0.49
𝑐 + 0.42
)
𝑓𝑟 = �
𝜀̇
10
�
𝑚
. �
𝜀̇
100
�
𝑚
2.4
. (
𝜀̇
1000
) 𝑚/15
𝑚 = (0.081𝐶 − 0.154)𝑇 − 0.019𝐶 + .207 +
0.027
𝐶+0.32
From the above values and graph we can conclude that the flow stresses for different steels
with different carbon percentages are nearly the same at the rolling conditions. [6]
Thus, considering the mean value of flow stress as 152Mpa, the deviatoric stress
components can be found out.
7.7 Calculation of deviatoric stress components
The deviatoric stress components are those which need to be exceeded at a given
conditions for changing the cross section of the work piece.
These components in the 3 directions x, y and z can be found by levy-mises flow rule
𝜎́ 𝑥 =
2
3
𝜎
𝜎̇ 𝑟
𝜀 𝑥̇
Figure 9.2: Temperature flow stress relation for steels at given strain rate

𝜎́ 𝑥 =
2
3
×
152
11.84
×9.049= 77.83 Mpa
𝜎́ 𝑦 =
2
3
𝜎
𝜎̇ 𝑟
𝜀 𝑦̇
𝜎́ 𝑦 =
2
3
×
152
11.84
× 11.08 = 95.07 Mpa
According to the assumption made earlier, the interstand tension is being neglected.
Thus, the back and front tensile forces are taken equal to zero.
7.8 Calculation of roll load, torque and power
7.8.1 Roll load
F = −2 ∫ 𝜎 𝑦 𝑏 𝑑𝑥
𝐿 𝑥
0
𝐹 = −2 � 95.07
63.56
0
×
26.72
2
�
2𝑥
63.56
−
𝑥2
63.562
𝑑𝑥
𝐹 = −126.810 KN
Negative sign indicates that the load is compressive in nature.
7.8.2 Roll torque
M= −4 ∫ 𝜎 𝑦 𝑏
𝐿 𝑥
0
(𝐿 𝑟 − 𝑥) 𝑑𝑥 + 𝑅 𝑒(𝐹1 − 𝐹2)
𝑀 = −4 � 95.07 ∗
27.62
2
�
2𝑥
63.56
−
𝑥2
63.562
(63.56 − 𝑥)
63.56
0
𝑑𝑥
𝑀 = 6841.6 Nm
7.8.3 Rolling power
𝑃 =
𝑀 ∗ 𝑉2
𝑅 𝑒
𝑃 =
6841.6∗1.32
0.164
= 55.07 KW
0 (Assumed)

The roll torque, load and power calculated about are required for reducing the area of the
work piece.
The torque and load are provided by 2 rollers, which are connected to 2 universal joints
shafts.
Thus, The load applied by each roll
= 0.5(126.81) Nm=63.4KN
And, Torque applied by each roll
=0.5(6841.6) Nm=3420.8 Nm
7.8.4 Power supplied by shaft
𝑃 =
2𝜋𝑁𝑇
60
𝑃 =
2𝜋∗79∗6841.6
60
= 56.6 Kw
Thus, the power lost = 56.6-55.07 = 1.53Kw

CHAPTER 08 VALIDATION OF THE RESULTS
8.1 Calculation of reactions at bearing
For finding the life of bearings it is necessary to calculate the load on the bearings. This
load is the reaction on the bearings due to the rolling load, torque, weight of shaft,
wobblers and other components.
Thus, modelling the shaft and wobblers as beam with supports at the two ends and finding
the reaction at bearings, which can be considered as hinges.
The reactions are as follows:
𝑅 𝐴 = 1424𝑁 and 𝑅 𝐵 = 1589.48𝑁
Max BM= -569979.7 N-mm
8.2 Calculating the min permissible diameter of the shaft (by ASME code)
𝜏 =
16 ∗ 103
𝜋𝐷3
∗ �(𝐾𝑡 𝑇)2 + (𝐾𝑏 𝑀)2
T =3420.8 Nm 𝐾𝑡 = 1.8
M =569.98 Nm 𝐾𝑏 = 2.6
𝜏 = min�0.3𝑠 𝑦𝑡, 0.18𝑠 𝑢𝑡�
For SAE 4340,
𝜏 = min(0.3 ∗ 470, 0.18 ∗ 689) = 124.02 Mpa
𝐷3
=
16 ∗ 103
𝜋 ∗ 124.02
× �(1.8 ∗ 3420.8)2 + (569.98 ∗ 2.6)2
𝐷3
= 260121.62 mm3
𝐷 = 63.84 mm< 140 mm (Minimum diameter of solid parts of shaft)
Therefore shaft is safe.

Modelling for working length of shaft using MDSolids 3.5,

8.3 Calculating the shear stress in hollow shaft due to torque and moment
𝐷 𝑚𝑎𝑥 =200 mm 𝐷 𝑚𝑖𝑛 = 160 mm
𝐾 =
𝐷𝑖
𝐷𝑜
=
160
200
= 0.8
𝜏 𝑚𝑎𝑥 =
16 × 103
𝜋 × 2003 × (1 − 0.84)
× �(1.8 × 3420.8)2 + (569.98 × 2.6)2
𝜏 𝑚𝑎𝑥 = 6.83 MPa < 124 MPa
Thus, the hollow part of shaft is also safe.

CHAPTER 09 CAD MODEL OF SHAFT AND OTHER PARTS
The Input CAD Model of the Shaft assembly has been designed using SolidWorks
(Version: 2013) and exported in .IGS Format. The Entire Shaft assembly consists of the
following components:
9.1 Main shaft assembly
The splines are provided for two purposes- one, for aiding in the length adjustment of the
shaft according to various applications; two, they prevent the relative sliding of the two
shaft parts.
In order to connect the universal joints to the gear box and the roller, ‘wobblers’ are
provided on either side of the main assembly.
9.2 Wobbler (Gear Box side)
This wobbler has two types of pads, namely ‘flat pads’
and ‘radial pads’ in its inner periphery. The pads are
made of fibre and serve the purpose of absorbing the
shocks created during the operation of the shaft.
Figure 9.1: (top) Main Shaft assembly. (Bottom) Exploded view
Figure 9.2: Wobbler (Gear box side)

9.3 Wobbler (Roller Side):
This wobbler is similar in construction to its gear
box counterpart, the addition being that it has a
‘locating pin’ which fits in a similar groove in the
roller. This ensures that there is a perfect
alignment between the roller and the shaft.
9.4 Yoke assembly with universal joints:
This assembly consists of split eye- type yoke
assembly, eye plate-type yoke assembly and
spider assembly comprising of bearings.
Figure 9.3: Wobbler (Roller side)
Figure 9.4: Eye Assembly
Figure 9.5: Exploded view of universal joint assembly

9.5 Yoke Pin:
The yoke pin is the main focus of this project. It is
fitted inside the hole in the split eye- type yoke and
extends up to the slot in the eye plate. Its main function
is to restrict the angle made by the universal joint; thus
preventing the joint from damage.
9.6 Needle Bearings:
The needle bearings used in this model is of grade IS
4215 RN1 - NB506225, meaning that the housing is
of 50mm inner diameter, 62mm outer diameter and of
thickness 25mm.
The needle bearings itself are arranged in two rows,
the specifications of the same being 6mm diameter
and 17.5mm in height.
The needle bearings are in direct contact with the spider arm (inner) as there are no inner
race in the housings. The need of two rows of bearings instead of one long bearing is
attributed to the fact that there is a lesser chance of failure by crushing of the bearing in a
two row arrangement.
9.7 Roller:
The rollers are the most vital components in any rolling mill. In this case, there are two
rollers, which are set apart by a small distance; while the billet passes between them. The
rollers are made from cast steel and have grooves on their surfaces. The curvature and the
depth of these grooves depend on the application. The outer diameter of the roller is
360.5mm and its surface has 5 grooves in it. One side of the roller is machined to fit inside
a similar geometry inside the wobbler.
Figure 9.6: yoke pin
Figure 9.7: Needle bearing
with housing

9.8 Spider Assembly:
This assembly consists of a ‘spider’ which has four
arms on which four needle bearing housings are
mounted. Two of these housings fit into the split eye-
type and the other two into eye plate type, which is
mutually perpendicular to the split eye- type yoke.
Figure 9.8: Roller.
Figure 9.9: Spider assembly
Figure 9.10: Complete shaft assembly

The Material details of the Assembly considered in Finite Element Model build is as
below:
Table 9.1: Materials of various components
Component Material
Young’s
Modulus
(MPa)
Poisson’s
Ratio
Density
(kg/m3
)
Shafts Steel 2.1 e 5 0.3 7850
Eye & Plates Steel 2.1 e 5 0.3 7850
Wobbler Steel 2.1 e 5 0.3 7850
Yoke Pin Steel 2.1 e 5 0.3 7850

CHAPTER 10 MESH GENERATION
10.1 Geometry Cleanup:
The imported CAD model is cleaned up for its geometry thereby forming a good input for
finite element modeling. Initially surfaces are developed from the solid components after
which the solids are removed as the finite elements are generated out from the surfaces.
The global clean-up tolerance is set as 0.01.
The model is checked for any free edges and are cleaned up using toggle, replace and
equivalence operations with appropriate clean up tolerances. The model is then verified for
missing surfaces which could be identified from free edges and new surfaces are created in
those locations. The model is then checked for non - manifold edges where there are more
than two surfaces sharing an edge, which might indicate incorrect connectivity. Duplicate
surfaces are also checked with a clean-up tolerance of 0.01 and then deleted.
Fillets of minor importance are removed thereby simplifying the geometry. Surfaces of
bolts, nuts and washers are removed as they are modelled with appropriate element types
during the process of finite element modelling.
Fillets of minor
detail are removed
Figure 10.1: Geometry clean-up - Removal of fillets of minor detail
Toggled Edge
Figure 10.2: Geometry clean-up – Toggled edges

10.2 Meshing of Components in HyperMesh 12.0:
Once the Geometry is cleaned up, all the surfaces are meshed with 2D Tria Elements (Tria
& R-Tria) of average size = 10mm to form a closed mesh. 3D Tetrahedral Elements are
created from the closed 2D mesh so as to form Solid components. Property collectors are
created for each component with PSOLID Card Image and assigned correspondingly.
Figure 10.3: Mesh model of
Shaft Assembly
Figure 10.4: Mesh model of Eye &
Plate Assembly
Figure 10.5: Mesh model of Wobbler
Assembly
Figure 10.6: Mesh model of Eye Plate
& Yoke Pin

10.3 Element Quality Check:
The geometric quality of all the 1D, 2D, 3D elements in the model is checked. The model
is also checked for proper connectivity and for duplicate elements.
Table 10.1: Element Quality Parameters
1 D elements
Free 1 D elements
Rigid loops
Double dependency
2 D elements
Warpage 15.00
Aspect 10.00
Length 2.00
Jacobian 0.5
Tria Minimum angle 20°
Tria Maximum angle 120°
3 D elements
Tet Collapse 0.2
Length 2.00
Tria Minimum angle 20°
Tria Maximum angle 120°
Figure 10.7: Mesh model of
Shaft Assembly

10.4 Boundary Conditions:
The DOFs of the wobblers are constrained by fixing the face of the wobblers on either sides. The
constraints are shown by blue triangles (Fig.)
10.5 Load Steps:
The Meshed assembly is analysed for the following:
1) SOL 103: Constrained Modal Analysis – for determining Natural Frequencies of
Assembly and Mode Shapes.
- EIGRL Card for first 4 Mass Normalized Modes are specified for performing Real
Eigen Value Analysis with LANCZOS method
2) SOL 101: Static Analysis – by applying Moment on the shaft, the areas of higher
stresses are identified.
Figure 12.9: 3D Element
Representation
Figure 12.10:
Traditional Element
Representation

CHAPTER 11 MODAL ANALYSIS
11.1 Introduction:
Modal analysis is the process of determining the inherent dynamic characteristics of a
system in forms of natural frequencies, damping factors and mode shapes, and using them
to formulate a mathematical model for its dynamic behaviour. The dynamics of a structure
are physically decomposed by frequency and position. It is based upon the fact that the
vibration response of a linear time-invariant dynamic system can be expressed as the linear
combination of a set of simple harmonic motions called the natural modes of vibration.
11.2 Mode shapes:
The formulated mathematical model in the process of modal analysis is referred to as the
modal model of the system. The natural modes of vibration are inherent to a dynamic
system and are determined completely by its physical properties (mass, stiffness, damping)
and their spatial distributions. Each mode is described in terms of its modal parameters:
natural frequency, the modal damping factor and characteristic displacement pattern,
namely mode shape. The mode shape may be real or complex. Each corresponds to a
natural frequency. The degree of participation of each natural mode in the overall
vibration is determined both by properties of the excitation source and by the mode shapes
of the system.
Mode 4
Mode 1 Mode 2
Mode 5
Mode 3
Mode 6
Figure 11.1: Mode Shapes

11.3 Single Degree Of Freedom:
A single-degree-of-freedom (SDOF) system is described by the following equation:
mẍ(t) + cẋ(t) +kx(t) = f(t)
where ‘m’ is the mass, ‘c’is the damping coefficient, and ‘k’is the stiffness. This equation
states that the sum of all forces acting on the mass ‘m’ should be equal to zero with f(t)is a
externally applied force, -mẍ(t)is the inertial force, -cẋ(t)is the (viscous) damping force
and -kx(t)is the restoring force. The variable x(t) stands for the position of the mass m with
respect to its equilibrium point, i.e. the position of the mass when f(t) = 0.
The transfer function H(s) between displacement and force, X (s) = H(s)F(s) , is given by,
𝐻(𝑠) =
1
𝑚𝑠2 + 𝑐𝑠 + 𝑘
The roots of the denominator of the transfer function, d(s) = ms2
+ cs+ k, are the poles of
the system. In mechanical structures, the damping coefficient c is usually very small
resulting in a complex conjugate pole pair, 𝜆 = −𝜎 ± 𝑖𝜔𝑑
The undamped natural frequency is given by
fn = ωn/2 𝜋 where 𝜔 𝑛 = �𝑘/𝑚 = |𝜆|
When a mass m is added to the original mass m of the structure, its natural frequency
decreases to, 𝜔 𝑛 = �(𝑘/(𝑚 + Δ𝑚). Although very few practical structures could
realistically be modelled by a SDOF system, the properties of such a system are important
because those of a more complex MDOF system can always be represented as the linear
Figure 11.2: SDOF system

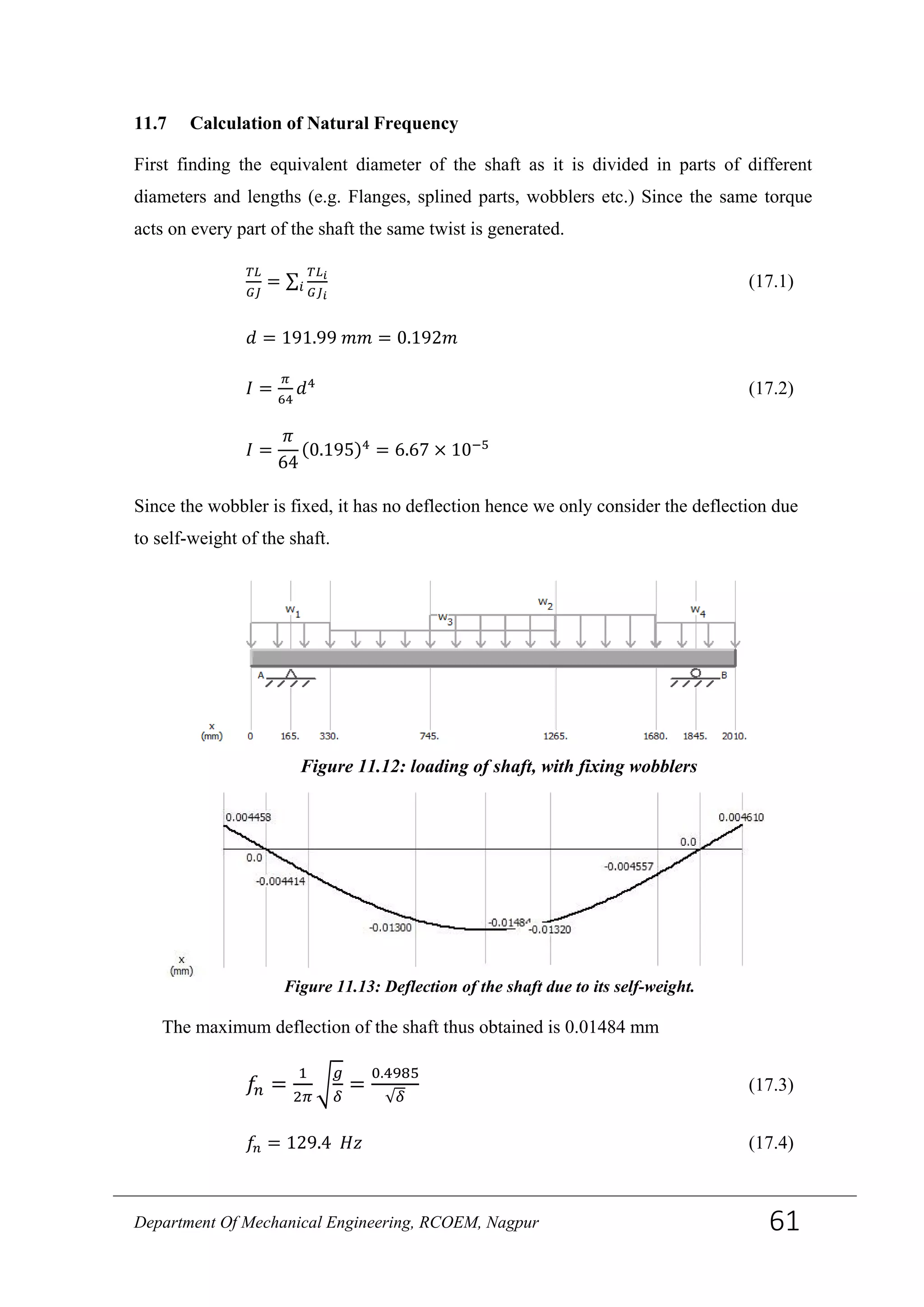
superposition of a number of SDOF characteristics (when the system is linear time-
invariant).
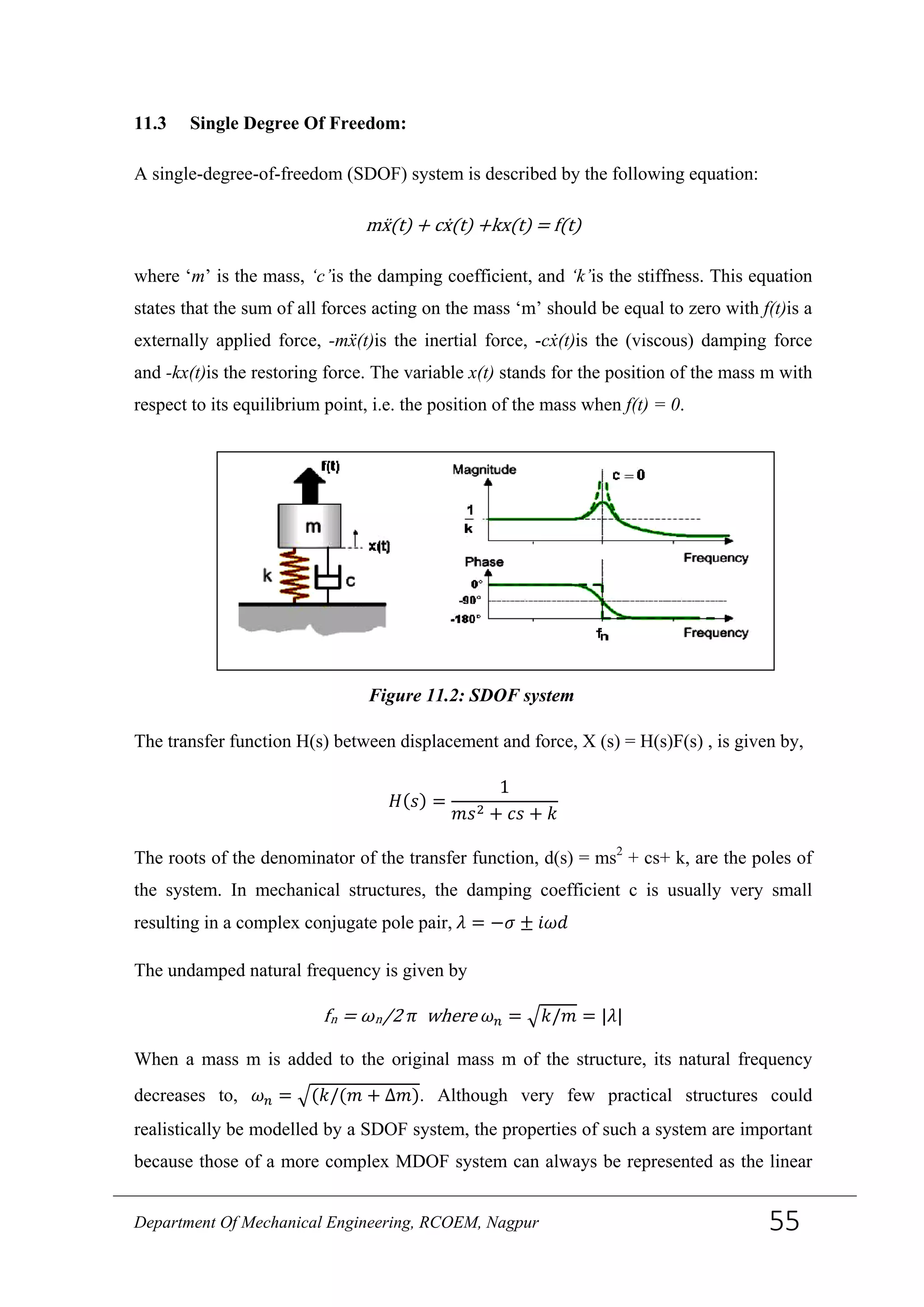
11.4 Multi Degree Of Freedom:
Multiple degree-of-freedom (MDOF) systems are described by the following equation:
Mẍ(t) + Cẋ(t) +Kx(t) = f(t)
The transfer function H(s) between displacement and force, X (s) = H(s)F(s) , is given by,
𝐻(𝑠) = [𝑀𝑠2
+ 𝐶𝑠 + 𝐾]−1
=
𝑁(𝑠)
𝑑(𝑠)
Where, N(s) = adj(Ms2 + Cs + K)
And, d(s) = det(Ms2 + Cs + K)
When the damping is small, the roots of the characteristic polynomial d(s) are complex
conjugate pole pairs, 𝜆 𝑚and𝜆 𝑚∗, m = 1…..N m, with Nmthe number of modes of the
system. The transfer function can be rewritten in a pole-residue form which is said to be
the “modal” model.
𝐻( 𝑠) = ∑
𝑅 𝑚
𝑠−𝜆 𝑚
𝑁 𝑚
𝑚=1 +
𝑅 𝑚∗
𝑠−𝜆 𝑚∗
The residue matrices Rm, m =1……Nm, are defined by, 𝑅 𝑚 = lim 𝑠→𝜆 𝑚
𝐻(𝑠)(𝑠 − 𝜆 𝑚)
It can be shown that the matrix R mis of rank one meaning that R mcan be decomposed
as,
Figure 11.3: MDOF system

with ᴪm a vector representing the “mode shape” of mode m. The full transfer function
matrix is completely characterized by the modal parameters, i.e. the poles,
λm = −σm ± iωd,m and the mode shape vectors ᴪm, m = 1……Nm.
11.5 Free – Free Analysis :
A free-free analysis is performed to extract the rigid body modes from the modeled
assembly. All constraints specified on the model are removed before performing the free –
free Analysis. This analysis is also used to check whether all the components are properly
connected with each other. The natural frequencies of the first six fundamental modes are
found approximate to be zero.
Figure 11.4: Mode 1(top): Translation about X- axis
Mode 2(bottom): Translation about Y- axis

Figure 11.6: Mode 4- Rotation about X- axis
Figure 11.7: Mode 5- Rotation about Y- axis
Figure 11.5: Mode 3- Translation about Z- axis

Figure 11.8: Mode 6- Rotation about Z- axis
11.6 Normal Modes Analysis:
With constraints at Eye Plate Bearing locations, the Natural Frequencies & Mode shapes of the
assembly are as follows:
Figure 11.9: (Top) Normal Mode 1, (bottom) Normal Mode 2

The mating surface of the pin
with the universal joint eye is
observed to be highly strained
because of the top – down
movement and hence has a
greater possibility for failure
when undergoing several
working cycles.
Figure 11.10: (Top) Normal Mode 3, (Bottom) Normal Mode 4
Figure 11.11: Strained areas of eye plate

11.7 Calculation of Natural Frequency
First finding the equivalent diameter of the shaft as it is divided in parts of different
diameters and lengths (e.g. Flanges, splined parts, wobblers etc.) Since the same torque
acts on every part of the shaft the same twist is generated.
𝑇𝐿
𝐺𝐽
= ∑
𝑇𝐿 𝑖
𝐺𝐽 𝑖
𝑖 (17.1)
𝑑 = 191.99 𝑚𝑚 = 0.192𝑚
𝐼 =
𝜋
64
𝑑4
(17.2)
𝐼 =
𝜋
64
(0.195)4
= 6.67 × 10−5
Since the wobbler is fixed, it has no deflection hence we only consider the deflection due
to self-weight of the shaft.
The maximum deflection of the shaft thus obtained is 0.01484 mm
𝑓𝑛 =
1
2𝜋
�
𝑔
𝛿
=
0.4985
√𝛿
(17.3)
𝑓𝑛 = 129.4 𝐻𝑧 (17.4)
Figure 11.12: loading of shaft, with fixing wobblers
Figure 11.13: Deflection of the shaft due to its self-weight.

Mode no. 1 2 3 4
Natural Frequency 121.9 122.3 305.5 313.9
Natural frequency by analytical calculation is equal to 129.4 Hz.
The error when compared with natural frequency of mode 2 is 5.8%.
11.8 Static Stress Analysis
With Constraints in place, Input
moment of value = 6400 Nm is applied
to the Main Shaft about X Direction
and Areas of High Stress Locations
(Von- Mises Stress) are determined.
It is found that the stress on the yoke
pin is 15 MPa on an average.
Compared with its yield stress of
210MPa, it is very less. So, the
possible conclusion is that the yoke pin
gets failed due to wear. Figure 11.14: Stressed areas of pin and eye
plate
Table 11.1: Natural frequency (by Hyper Mesh)

CHAPTER 12 CONCLUSION AND SUGGESTIONS
12.1 Conclusion
 From the above analysis, the conclusion drawn is that the yoke pin has very less
stresses acting on it. The stresses are of the magnitude of 15MPa on an average.
The pin material is SAE 1045. The stresses for the pin material are bearable and
the pin is safe in crushing, tension, shear, and bending. The Yoke Pin mainly fails
due to wear.
 The hole for the pin has stresses equal to 2MPa. The material is strong enough to
withstand these stresses.
 Both the pin and the eye plate hole are wearing out due to the jerking of the shaft.
The jerks in the shaft are mainly caused due to striking of the billet, compression
of the air gaps in billet, uneven cross sections, surface irregularities on the billet,
etc.
 The pin and the hole in the eye plate need some treatment for wear resistance.
 The natural frequency of the shaft comes out to be 122 Hz. The error when
compares with software results is 5.8%.
12.2 Modifications for reducing the wear of the components:
 Use of bush between the pin and the hole, which will itself wear out and hence
save the wear prone components of the assembly.
o The use of bush will reduce the time for repairs. Just the bush needs to be
replaced.
 Use of press fit covering on the pin and hole.
o This will prove to be very much time effective.
o Just changing the covering on the pin and hole will reduce the repair time
and increase the time between repairs.
o The material for the covering may be suitably selected depending on the
stand position, failure frequency etc.
 Review of the welding materials and the process currently used to repair the
damaged parts.
o Using different materials for filling metal in the gap formed in the eye plate
hole.
o The time required for the repair may not change by doing so, but the time
between the failures can certainly increase.

CHAPTER 13 FUTURE SCOPE
The project can be further expanded in various horizons.
The modifications suggested in the section 12.2 needs to be analysed thoroughly. The
modifications must be analysed, in terms of cost, time effectiveness, worker adaptability
etc.
Further dimensions for the project can be:
 Design of the bush between the pin and the hole, which will wear out and hence
save the wear prone components of the assembly. The factors which need to be
considered for this:
o Design changes.
o The material of the bush.
o The cost analysis.
 Design of the press fit covering on the pin and hole. The factors to be considered
are:
o Design modifications.
o Stress analysis of the new design.
o The tolerances to be given for the components will be a major concern.
 Review of the welding materials and the process currently used to repair the
damaged parts.
o Different welding materials need to be used on the pin and the hole to
increase the time between two failures.
 Reducing the shocks and jerks coming on the shaft.
o The ways to reduce the shock need to be developed.
o At least way to transmit the shock to some different component which is
strong enough to take them needs to be developed.

APPENDIX (SOFTWARES USED)
SOLIDWORKS 2013 (CAD Modelling)
SolidWorks is a Para solid-based solid modeller, and utilizes a parametric feature-
based approach to create models and assemblies.
Parameters refer to constraints whose values determine the shape or geometry of the
model or assembly. Parameters can be either numeric parameters, such as line lengths or
circle diameters, or geometric parameters, such as tangent, parallel, concentric, horizontal
or vertical, etc. Numeric parameters can be associated with each other through the use of
relations, which allow them to capture design intent.
Building a model in SolidWorks usually starts with a 2D sketch (although 3D sketches are
available for power users). The sketch consists of geometry such as points, lines, arcs,
conics (except the hyperbola), and splines. Dimensions are added to the sketch to define
the size and location of the geometry. Relations are used to define attributes such as
tangency, parallelism, perpendicularity, and concentricity. The parametric nature of
SolidWorks means that the dimensions and relations drive the geometry, not the other way
around. The dimensions in the sketch can be controlled independently, or by relationships
to other parameters inside or outside of the sketch.
In an assembly, the analog to sketch relations are mates. Just as sketch relations define
conditions such as tangency, parallelism, and concentricity with respect to sketch
geometry, assembly mates define equivalent relations with respect to the individual parts
or components, allowing the easy construction of assemblies. SolidWorks also includes
additional advanced mating features such as gear and cam follower mates, which allow
modelled gear assemblies to accurately reproduce the rotational movement of an actual
gear train.
Finally, drawings can be created either from parts or assemblies. Views are automatically
generated from the solid model, and notes, dimensions and tolerances can then be easily
added to the drawing as needed. The drawing module includes most paper sizes and
standards (ANSI, ISO, DIN, GOST,JIS, BSI and SAC).

HYPERMESH 12.0 (For Meshing)
Altair HyperMesh is a high-performance finite element pre-processor to prepare even the
largest models, starting from import of CAD geometry to exporting an analysis run for
various disciplines.
HyperMesh enables engineers to receive high quality meshes with maximum accuracy in
the shortest time possible. A complete set of geometry editing tools helps to efficiently
prepare CAD models for the meshing process. Meshing algorithms for shell and solid
elements provide full level of control, or can be used in automatic mode. Altair’s
BatchMeshing technology meshes hundreds of files precisely in the background to match
user-defined standards. HyperMesh offers the biggest variety of solid meshing capabilities
in the market, including domain specific methods such as SPH, NVH or CFD meshing.
A long list of CAD formats ensures a high level of CAD interoperability. Altair’s
connector technology automatically assembles individual parts with their Finite Element
representation. HyperMesh is entirely customizable. A extensive API library can be used
to automate repeating tasks or do complicated math operations for model generation.
With a focus on engineering productivity, HyperMesh is the user-preferred environment
for:
• Solid Geometry Modeling
• Shell Meshing
• Model Morphing
• Detailed Model Setup
• Surface Geometry Modeling
• Solid Mesh Generation
• Automatic Mid-surface Generation
• Batch Meshing
MDSolids (SFD, BMD Solver)
MDSolids is multi-faceted software that offers numerical, descriptive, and visual results
and details that illustrate and explain many types of problems involving stress and strain,
axial members, beams, columns, torsion members, truss analysis, and section properties
calculations. MDSolids' graphical user interface makes the software visually appealing,
easy-to-use, and very intuitive, so that students can focus on the problem-solving concepts
rather than on the operation of the software.

NASTRAN (Solver)
NASTRAN is a finite element analysis (FEA) program that was originally developed
for NASA inthe late 1960s under United States government funding for the Aerospace
industry. The Mac Neal-Schwendler Corporation (MSC) was one of the principal and
original developers of the public domain NASTRAN code. NASTRAN source code is
integrated in a number of different software packages, which are distributed by a range of
companies.
MSC Nastran is an HPC enabled structural analysis application used by engineers to
perform static, dynamic, and thermal analysis across the linear and nonlinear domains,
complemented with automated optimization and award winning embedded fatigue analysis
technologies.
From the high performance computing capability to the high degree of certainty it
delivers, MSC Nastran is engineered to give a heightened awareness of component
behaviour.
• Accurately and quickly predict complex product behaviour.
• Find design conflicts early in the design cycle.
• Reduce the number of design changes.
• Make trade off studies for performance and reliability.
Capabilities:
Predict product life, optimize designs.
Advanced nonlinear capabilities
Multi-physics simulation
Dynamic response of structural designs
MSC’s integrated solution for linear and nonlinear calculations facilitates reuse of models
which saves a lot of time in pre- processing and enables us to standardize the data
exchange formats for body models when collaborating with other departments or external
suppliers”

APPENDIX (ABOUT SUNFLAG IRON AND STEEL LTD.)
Sunflag Iron and Steel Co. Ltd. is a prestigious unit of the SUN FLAG GROUP. It has set
up a state-of-art integrated plant at Bhandara, India. The plant has a capacity to produce
360,000 tons per annum of high quality special steel using liquid pig iron and sponge iron
as basic inputs.
Sunflag Steel caters to the demands of various core sector industries like Automobiles,
Railways, Defence, Agriculture, and Engineering Industry and approved by all
International & National OEM.The specialty steels being produced is as per Indian and
International Standards confirming to DIN / SAE / AISI / ASTM /EN, JIS, GOST , IS and
Honda Motors patented grades.
The plant comprises 2,62,000 tons per annum Direct Reduction Plants, to produce sponge
iron for captive consumption in the Steel Melting Shop. This shop comprises a 50/60 tons
ultra-high power Electric Arc Furnace with Eccentric bottom arrangement; Ladle refining
furnace, Tank Degassing and Bloom/Billet double radius caster with AMLC & EMS and
T type tundish. The billets produced at the steel melting shop are rolled at the
Mannesmann Demag Designed ultra-modern 20 stand Continuous mill. This mill has a
dual fuel type walking hearth reheating furnace, quick roll-changing facilities, a 65 meters
long walk and wait type modern cooling bed and above all computerized process control
linking and controlling the various stages.
Within a short period of its inception in 1989, the SUNFLAG STEEL has established
itself as a major global force. This modern complex pulsating with world-class
technology, expert human resources and a commitment to excellence, has created a
distinct niche in Alloy Steel, Stainless Steel & Micro alloyed Steel and attained the
position of market leader in the segment. Today SUNFLAG STEEL has also embarked on
an export thrust and is regularly receiving prestigious orders from Japan and many other
Far East, Afro-Asian and Middle-East countries.
A captive Power Plant of 30 MW capacity has already been commissioned using waste
gases.

Bar and Section Mill (BSM): The 60 tonnes per hour, 20 stand, 2 high continuous
Mannesmann designed rolling mill is equipped with duel fuel walking hearth type re-
heating furnace, process control through ABB automation, Online gauging system, Closed
circuit TV system for billet and bar movements. Variable Reduction mill (VRM) is being
installed after stand # 20 to produce close tolerance product. Product sizes - Round (15-53
mm diameter), Hex (13 to 38.5 mm), WRD (12 to 38 mm diameter), WRB (4.6 to 16 mm)

REFERENCES
Patents
1. Edmund P. Morewood, Improvement in Coating Iron and Copper, U.S. Patent 3746,
Sept. 17, 1844.
Books
2. Kalpakjian, Schmid, “Manufacturing Processes for Engineering materials”, 5th ed.
2008, Pearson Education ISBN No. 0-13-227271-7.
3. George E. Dieter, Jr. “Mechanical Metallurgy”. McGRAW-HILL BOOK COMPANY
4. Youngseog Lee, Rod And Bar Rolling, Theory and Applications, Mercel Dekker Inc.
5. George T. Halmos, Roll Forming handbook, CRC Press, Taylor and Francis Group,
2006.
6. Lenard J.G., Piterzyk M., Cser, L, “Mathematical and Physical simulation of the
properties of hot rolled products”, Elsevier Science Ltd., 1999.Pp. 74-76
Papers
7. Paluh J H, Hills G R, Wojtkowski T C. Design and selection of universal shafts for
rolling mills
8. Mills, Allan, “Robert Hooke’s ‘universal joint’ and its application to sundials and the
sundial clock”, Notes and records of the Royal Society, 2007.
9. S.M.A. Sheikh, “Analysis of universal coupling under different torque condition”,
International journal of engineering science & advanced technology, 2012, Volume-2,
Issue-3, 690 – 694.
10. Laila S. Bayoumia, Youngseog Lee “Effect of interstand tension on roll load, torque
and work piece deformation in the rod rolling process” Journal of Materials Processing
Technology 145 (2004) 7–13
11. Youngseog Lee", Hong Joon Kim Sang Moo Hwang “An Approximate Model for
Predicting Roll Force in Rod Rolling” KSME International Journal, VoL16 No.4,
2002, pp. 501-511.
12. U. K. Yoo, J. B. Lee, J. H. Park3 and Y. Lee Analytical model for predicting the
surface profile of a work piece in round-to-2–R and square-to-2–R oval groove rolling
Journal of Mechanical Science and Technology 24 (11) (2010) 2289~2295.
13. Stuart H. Loewenthal, “Design of Power-Transmitting Shafts”, NASA Reference
Publication 1123 July 1984.
14. Ahmed Said , J.G. Lenard , A.R. Ragab , M. Abo Elkhier “The temperature, roll force
and roll torque during hot bar rolling”, Journal of Materials Processing Technology 88
(1999) 147–153
15. S M Byon, S I Kim and Y Lee “Predictions of roll force under heavy-reduction hot
rolling using a large-deformation constitutive model”, Journal of Proc. Instn Mech.
Engrs Vol. 218 Part B: J. Engineering Manufacture
16. S M Byon, S I Kim and Y Lee “ study on constitutive relation of AISI 4140 steel
subject to large strain at elevated temperatures “, journal of Materials Processing
17. “Universal Joint Shafts and Hirth Couplings” journal of voith company issue dated
MAY 2011

18. Gordan.R.Johnson , William cook”a constituted model and data for metals subjected to
high strain , large strain and high tempreture”, ASME journal of engineering material
and technology dated January 1983 vol.119
19. Alberto Moreira Jorge Junior, Oscar Balancin ,”Prediction of Steel Flow Stresses
under Hot Working Condition” journal of Materials Research, Vol. 8, No. 3, 309-315,
2005
20. Ahmed Said , J.G. Lenard , A.R. Ragab , M. Abo Elkhier ,” The temperature, roll force
and roll torque during hot bar rolling” in Journal of Materials Processing Technology
88 (1999) 147–153
21. S. Vaynman, M.E. Fine, S. Lee and H.D. Espinosa, “Effect of strain rate and
temperature on mechanical properties and fracture mode of high strength precipitation
hardened ferritic steels” in ScriptaMaterialia 55 (2006) 351–354
22. Magnus Holmberg, “prediction of roll torque in hot rod and wire rolling” Örebro
University Department of technology Örebro, Sweden
Web sites
23. http://www.sdp-si.com/D757/couplings3.htm
24. http://nptel.iitm.ac.in/courses/Webcourse-contents/IIT%20Kharagpur/Machine%20
design1/pdf/mod8les1.pdf
25. http://www.siderurgicasevillana.com/en/process#
26. http://asm.matweb.com/search/SpecificMaterial.asp?bassnum=M434AE
27. http://en.wikipedia.org/wiki/SolidWorks
28. http://www.engineeringpathway.com/engpath/ep/learning_resource/summary/Summar
y?id=8ADB2955-03F0-49D7-B39F-46E71325E3EC
29. http://www.sunflagsteel.com/

PROJECTEES
Ankit Anand
Contact number: 9595486050
Email: ankit0612@gmail.com
Mukesh Mohan
Email: mukesh.mohan18@gmail.com
Mohit Kathoke
Email: mohitkathoke@gmail.com
Sughosh Deshmukh
Email: sughosh.deshmukh@gmail.com
Vasukarna Jain
Email: vkarnajain@gmail.com

GROUP PHOTO
Projectees with Guide Prof. G. R. Nikhade (fourth from left)

DESIGN ANALYSIS OF UNIVERSAL JOINT SHAFT FOR ROLLING MILLS

More Related Content

What's hot

Viewers also liked

Similar to DESIGN ANALYSIS OF UNIVERSAL JOINT SHAFT FOR ROLLING MILLS

Recently uploaded

DESIGN ANALYSIS OF UNIVERSAL JOINT SHAFT FOR ROLLING MILLS