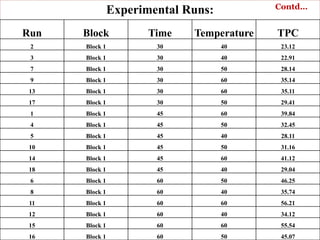
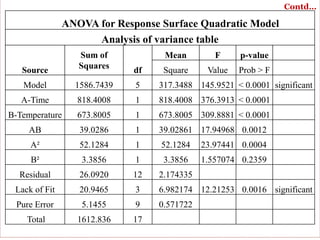
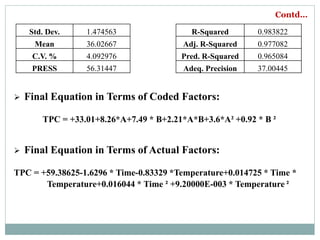
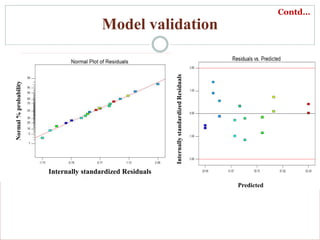
This document discusses Response Surface Methodology (RSM) in the food sector, highlighting its applications, including improving system performance and optimizing food processes. It provides a detailed example of the methodology applied to optimizing phenolic content in papaya leaf extract through experimental design and analysis of variance. The document also addresses challenges in RSM application, emphasizing the importance of selecting appropriate variable ranges and polynomial models.

1. “Response Surface Methodology”
(In the food Sector)
Presented by : Prakash Kumar
(Ph.D. Research Scholar, AGFE,
IIT-Kharagpur, India)
prakashfoodtech@gmail.com

2. Response Surface Methodology (RSM)
 Why? RSM in food Sector
 RSM application
 Challenges of applying RSM in food sector
RSM is the collection of Mathematical and
Statistical techniques useful the modeling
and analysis of problems in which a
response of interest is influenced by
several variables and the objective is to
optimize this responses.
- Douglas C. Montgomery (8th edition, 2015, p. 478 )

3. Why? RSM in the Food Sector
 To improve system performance
 For maximizing yield
 To enhance process efficiency without increasing cost and time
 For optimization of the food processes
 For designing, developing, and improving processes where a
response or responses are affected by several variables
 Application : extraction of oil, protein, phenolic compounds,
pigments, polysaccharides, hydrocolloids etc., manufacturing of
gluten free bread, biscuits, soy-coffee beverages, low caloric mixed
fruit jam, extruded food snacks, cream, walnut oil-in-water beverage
emulsion, homogenized infant foods, sweet potato based pasta etc.

4. RSM application:
 Problem statement :To find the effect of ultrasonic extraction
time and temperature on the total phenolic content (TPC) of Papaya
leaf extract
• Phenolic compounds are susceptible to high temperature
• Extraction of phenolic is accelerated at high temperature
• Selection of time and temperature levels for experimentation:
• Time: 30 min, 45 min and 60 min (3 levels)
• Temperature: 40°C, 50°C and 60°C (3 levels)
• Selection of experimental design: Full Factorial
• Response variable
Number of experiments: 32 =9*2 (2 replications) =18 runs

5. Run Block Time Temperature TPC
2 Block 1 30 40 23.12
3 Block 1 30 40 22.91
7 Block 1 30 50 28.14
9 Block 1 30 60 35.14
13 Block 1 30 60 35.11
17 Block 1 30 50 29.41
1 Block 1 45 60 39.84
4 Block 1 45 50 32.45
5 Block 1 45 40 28.11
10 Block 1 45 50 31.16
14 Block 1 45 60 41.12
18 Block 1 45 40 29.04
6 Block 1 60 50 46.25
8 Block 1 60 40 35.74
11 Block 1 60 60 56.21
12 Block 1 60 40 34.12
15 Block 1 60 60 55.54
16 Block 1 60 50 45.07
Experimental Runs: Contd…

6. ANOVA for Response Surface Quadratic Model
Analysis of variance table
Source
Sum of
Squares df
Mean F p-value
Square Value Prob > F
Model 1586.7439 5 317.3488 145.9521 < 0.0001 significant
A-Time 818.4008 1 818.4008 376.3913 < 0.0001
B-Temperature 673.8005 1 673.8005 309.8881 < 0.0001
AB 39.0286 1 39.02861 17.94968 0.0012
A² 52.1284 1 52.1284 23.97441 0.0004
B² 3.3856 1 3.3856 1.557074 0.2359
Residual 26.0920 12 2.174335
Lack of Fit 20.9465 3 6.982174 12.21253 0.0016 significant
Pure Error 5.1455 9 0.571722
Total 1612.836 17
Contd…

7. Std. Dev. 1.474563 R-Squared 0.983822
Mean 36.02667 Adj. R-Squared 0.977082
C.V. % 4.092976 Pred. R-Squared 0.965084
PRESS 56.31447 Adeq. Precision 37.00445
 Final Equation in Terms of Coded Factors:
TPC = +33.01+8.26*A+7.49 * B+2.21*A*B+3.6*A² +0.92 * B ²
 Final Equation in Terms of Actual Factors:
TPC = +59.38625-1.6296 * Time-0.83329 *Temperature+0.014725 * Time *
Temperature+0.016044 * Time ² +9.20000E-003 * Temperature ²
Contd…

8. Model validation
Normal%probability
Internally standardized Residuals
InternallystandardizedResiduals
Predicted
Contd…

9. Predicted
Actual
InternallystandardizedResiduals
Run Number
Contd…

10. A-TimeB-Temp.
TPC
A-Time
B-Temperature
3-D response surfaceContour response surface
Contd…

11. Challenges of applying RSM in the food sectors
 Correct choice of the range of independent variables : Enough
preliminary work or experience is needed to select the appropriate
range of each factor, which directly affect the success of RSM
optimization.
 Correct selection of the polynomial model: A second order equation
is used commonly. If the trend of the responses in the studied range
of factors is not suitable to depict with second-order equation, the
range of independent variables or the form of the dependent should
be transformed to suitable form, in which the trend of the responses
could be depicted with this equation. The RSM approach needs to
be regressed with a polynomial equation.

12.  The number of terms in polynomial equation is limited to number of
design points, as well as choice of the suitable polynomial equation
can be very laborious because each response needs its own distinct
polynomial equations. Thus, the accuracy of the RSM modeling can
be increased through combining with other modeling techniques
such
as Artificial Neural Network (i.e., ANN).
 ANN present an option to the polynomial regression method
as a modeling approach.
 ANN are presented usually as systems of inter-connected
neurons which can compute values from inputs, and are
capable of machine learning as well as pattern recognition
giving to their adaptive nature. This approach presents an
interesting chance to preparing non-linear modeling for
response surface and optimization of food industry processes.

13. References:
 YANG, W. X., & GAO, Y. X. (2005). Response surface methodology
& its application in food industry [J]. China Food Additives, 2(2), 68-71.
 Erbay, Z., & Icier, F. (2009). Optimization of hot air drying of olive
leaves using response surface methodology. Journal of food
engineering, 91(4), 533-541.
 Montgomery, D. C. (2015). Design and analysis of experiments.
John wiley & sons.

14. THANK YOU