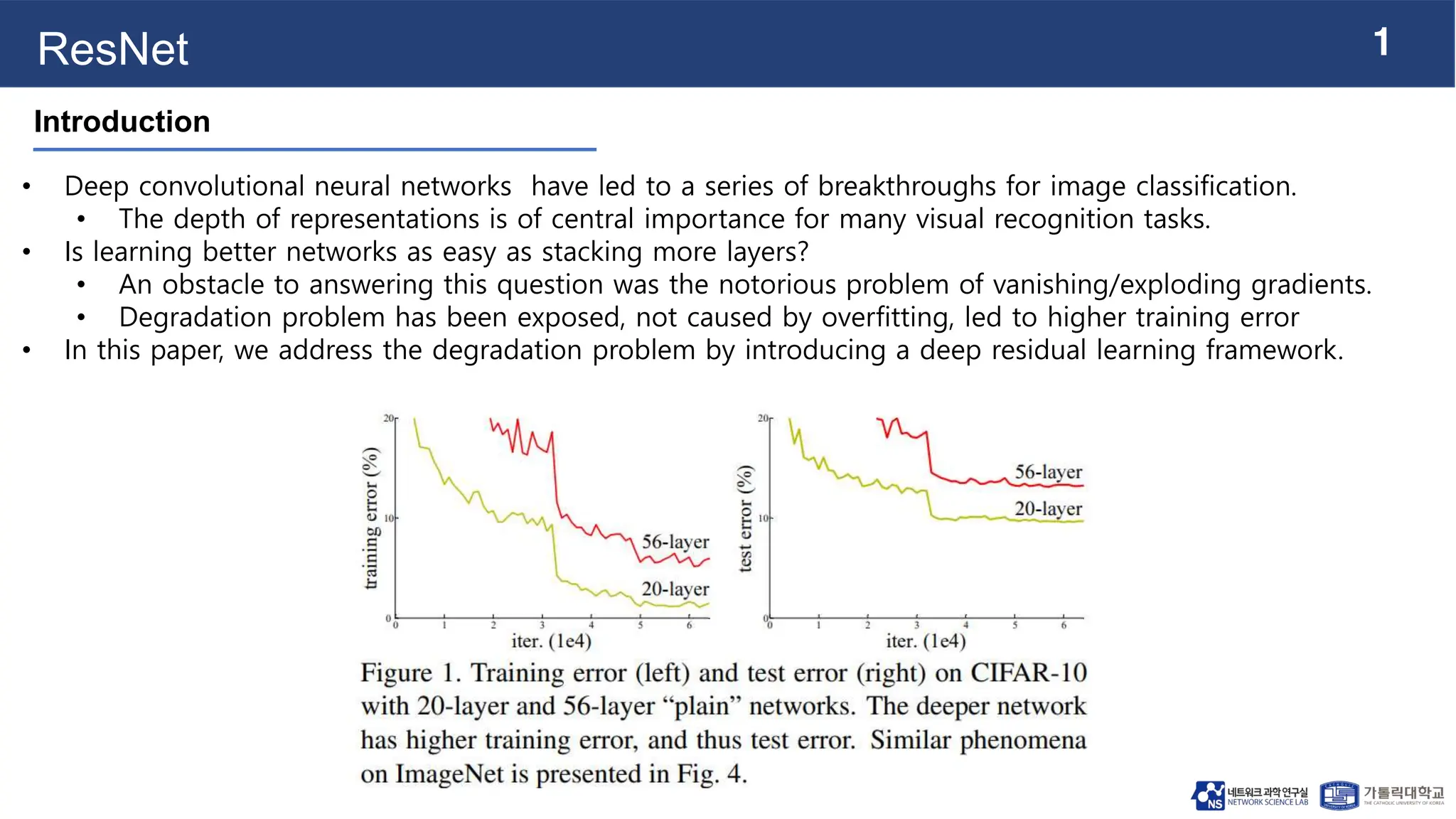
This document summarizes a paper on ResNet (Residual Neural Networks). It introduces residual learning frameworks to address degradation problems in training very deep convolutional neural networks. Residual learning frameworks utilize shortcut connections that feed the input directly to later layers, allowing networks to learn residual functions rather than unreferenced functions. This formulation eases the training of very deep networks and produces results substantially better than previous networks on image classification tasks.





![6
ResNet
• Evaluate our method on the ImageNet 2012 classification dataset [36] that consists of 1000 classes.
• Evaluate both top-1 and top-5 error rates.
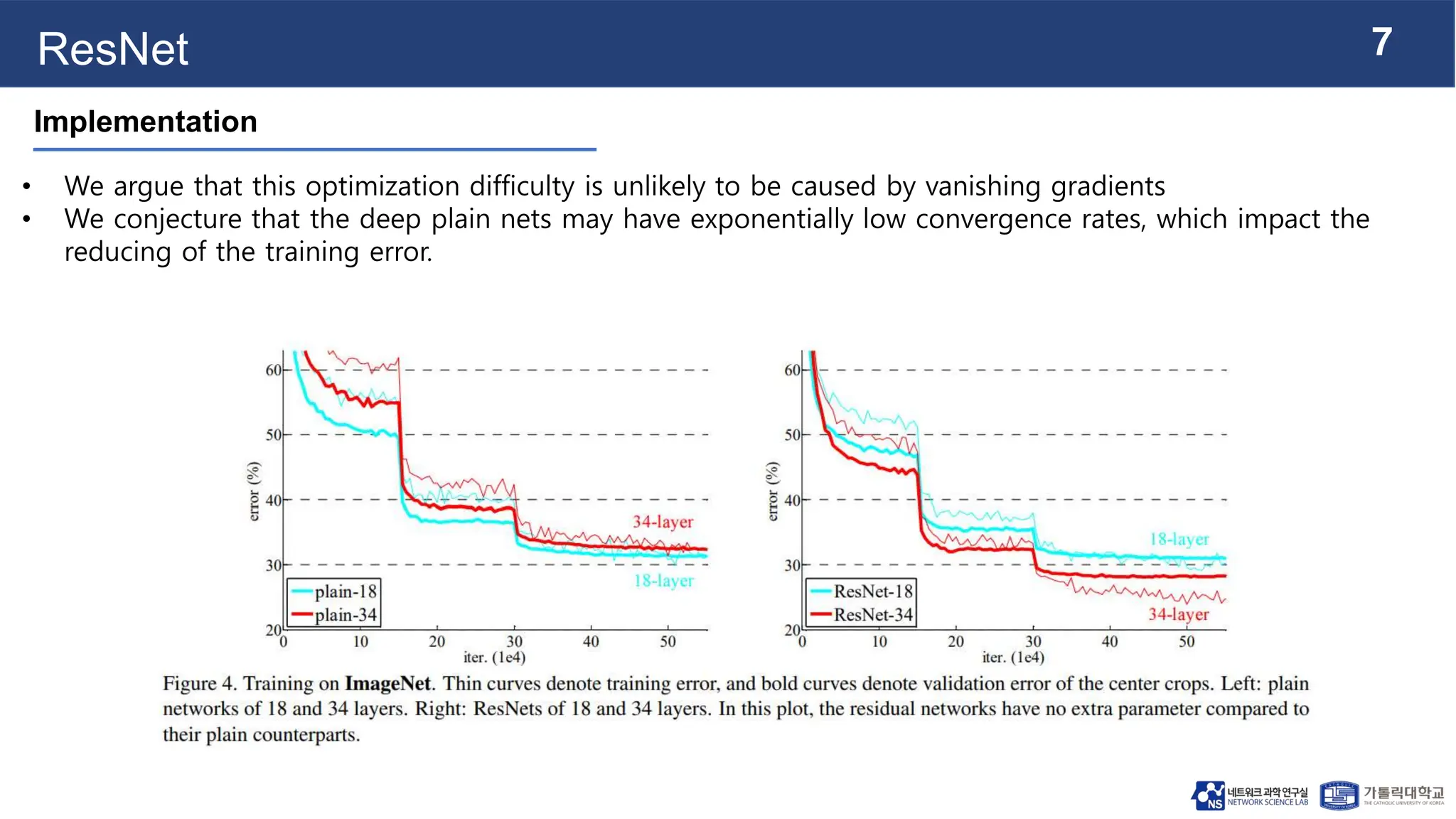
Implementation](https://image.slidesharecdn.com/231030mslabseminar-231106094618-60d757a7/75/ResNet-pptx-7-2048.jpg)