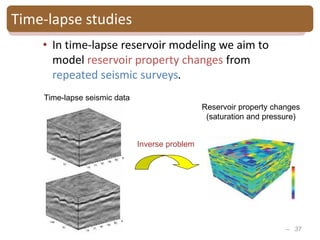
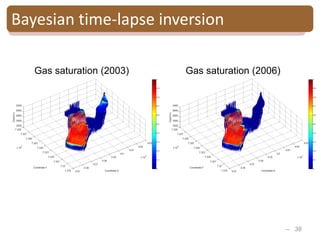
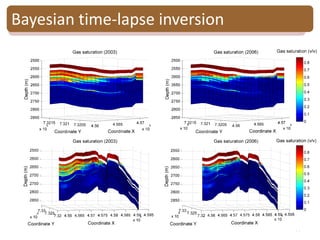
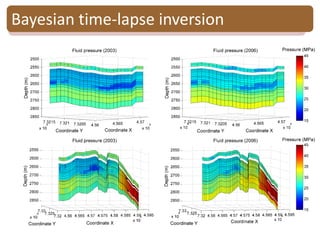
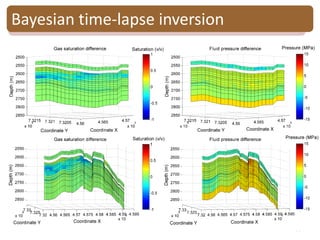
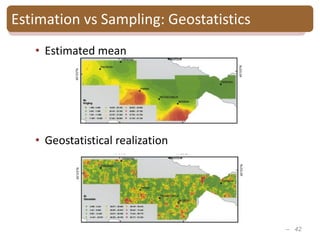
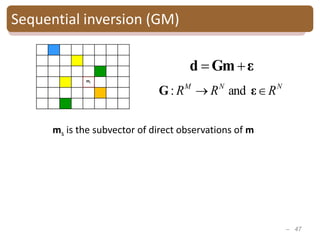
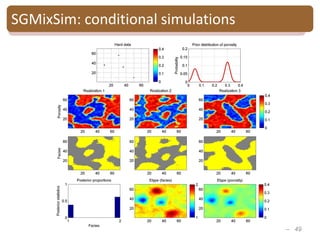
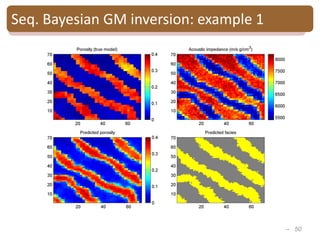
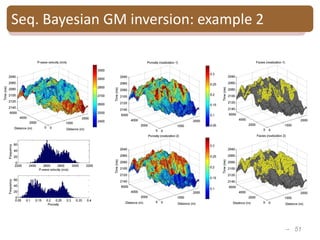
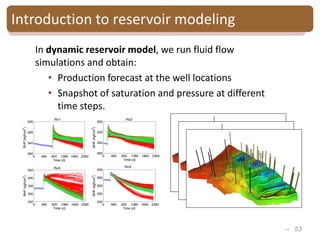
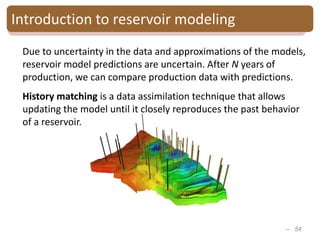
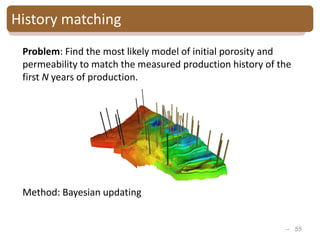
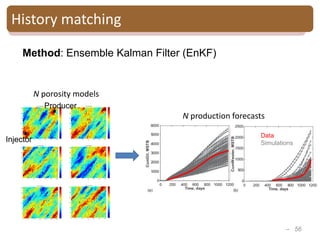
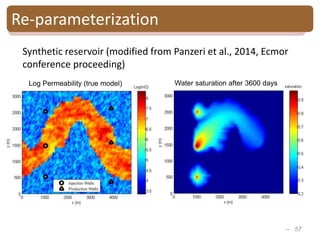
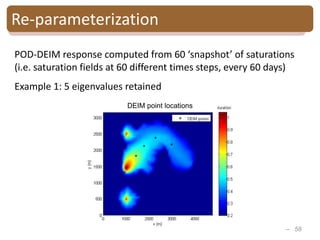
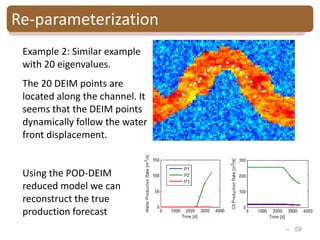
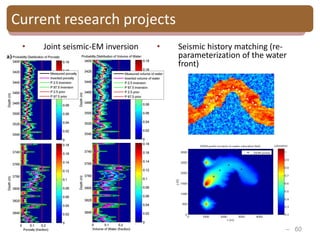
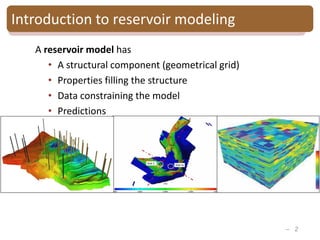
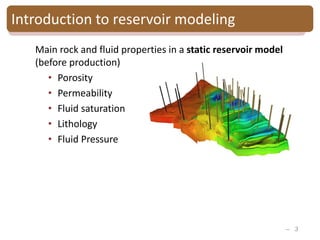
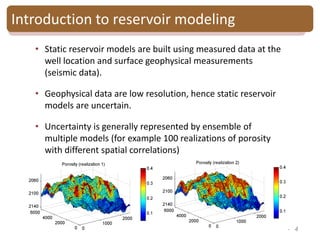
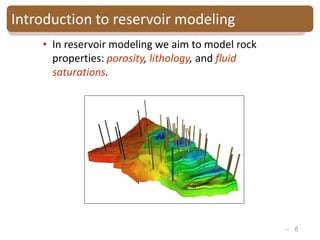
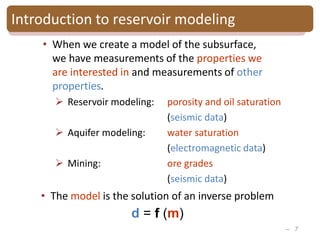
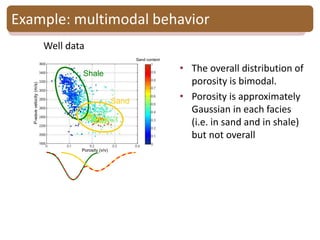
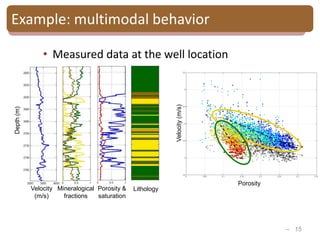
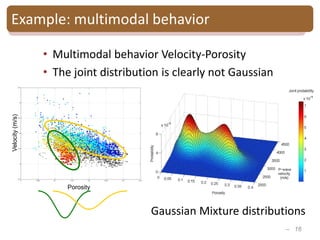
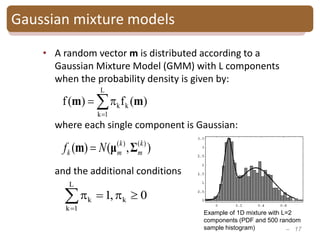
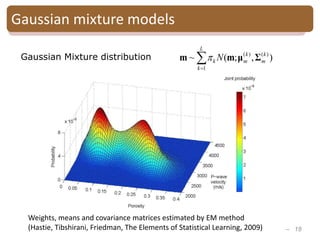
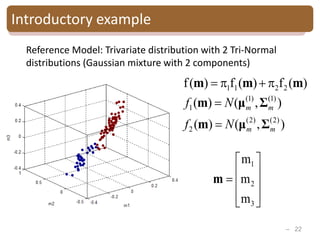
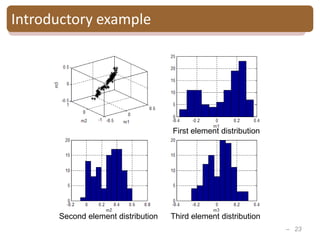
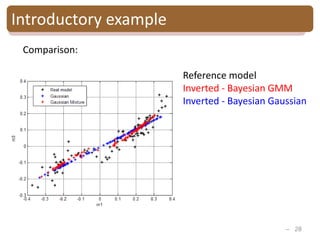
The document provides an introduction to Bayesian inverse theory and its applications in subsurface characterization and reservoir modeling. It discusses how Bayesian inversion can be used to estimate reservoir properties like porosity and saturation from seismic data by treating the inverse problem as estimating the posterior distribution given prior information and measurements. It also describes how the method can be extended to handle multimodal distributions using Gaussian mixture models. Further applications discussed include time-lapse inversion to estimate property changes over time and history matching to update reservoir models based on production data.

1. Bayesian inverse theory
for subsurface characterization and
data assimilation problems
Dario Grana
Department of Geology and Geophysics and School of Energy Resources
University of Wyoming
Quebec City, Canada – 18 March 2015

2. Introduction to reservoir modeling
A reservoir model has
• A structural component (geometrical grid)
• Properties filling the structure
• Data constraining the model
• Predictions
– 2

3. Introduction to reservoir modeling
– 3
Main rock and fluid properties in a static reservoir model
(before production)
• Porosity
• Permeability
• Fluid saturation
• Lithology
• Fluid Pressure

4. Introduction to reservoir modeling
• Static reservoir models are built using measured data at the
well location and surface geophysical measurements
(seismic data).
• Geophysical data are low resolution, hence static reservoir
models are uncertain.
• Uncertainty is generally represented by ensemble of
multiple models (for example 100 realizations of porosity
with different spatial correlations)
– 4

5. – 5
Outline
• Bayesian inversion
• Bayesian time-lapse inversion
• Geostatistical sampling
• History matching

6. Introduction to reservoir modeling
– 6
• In reservoir modeling we aim to model rock
properties: porosity, lithology, and fluid
saturations.

7. Introduction to reservoir modeling
– 7
• When we create a model of the subsurface,
we have measurements of the properties we
are interested in and measurements of other
properties.
 Reservoir modeling: porosity and oil saturation
(seismic data)
 Aquifer modeling: water saturation
(electromagnetic data)
 Mining: ore grades
(seismic data)
d = f (m)
• The model is the solution of an inverse problem

8. Introduction to reservoir modeling
– 8
• In reservoir modeling we aim to build models of
rock properties.
• Rock properties cannot be directly measured away
from the wells. The main source of information are
seismic data.
Inverse problem
Seismic data Porosity

9. – 9
Introduction: geophysical inverse problems
• There are various approaches for quantitative
estimation of reservoir properties from seismic
data:
 Linear or non linear regression
 Bayesian methods
 Stochastic optimization methods
• Spatial variations in reservoir properties and inter-
dependence between different properties are
complex to model.
• The probabilistic framework is ideally suited to
model the uncertainty.

10. – 10
Introduction: geophysical inverse problems
• Many inverse problems are solved by using a
Bayesian approach

11. – 11
Introduction: geophysical inverse problems
• Bayesian approach:
• Prior distribution: prior knowledge of the model (e.g.
geological information, nearby fields)
• Likelihood function: probabilistic information of the
physical model linking data and model
• Posterior distribution: probabilistic information
combining the prior and the likelihood
Prior
Likelihood
Posterior

12. – 12
Introduction: geophysical inverse problems
• Many inverse problems are solved by using a
Bayesian approach and assuming a linear (or
linearized) physical model and a Gaussian
distribution of the model.

13. – 13
Introduction: geophysical inverse problems
• We present a Bayesian inversion method based
on Gaussian mixture distributions.
• Many inverse problems are solved by using a
Bayesian approach and assuming a linear (or
linearized) physical model and a Gaussian
distribution of the model.

14. Example: multimodal behavior
Well data
P-wavevelocity(m/s)
Porosity (v/v)
Sand content
• The overall distribution of
porosity is bimodal.
• Porosity is approximately
Gaussian in each facies
(i.e. in sand and in shale)
but not overall
Shale
Sand

15. – 15
Velocity(m/s)
Porosity
• Measured data at the well location
Depth(m)
Velocity
(m/s)
Mineralogical
fractions
Porosity &
saturation
Lithology
SummaryExample: multimodal behavior

16. Velocity(m/s)
Porosity
– 16
Example: multimodal behavior
Gaussian Mixture distributions
• Multimodal behavior Velocity-Porosity
• The joint distribution is clearly not Gaussian

17. – 17
• A random vector m is distributed according to a
Gaussian Mixture Model (GMM) with L components
when the probability density is given by:
where each single component is Gaussian:
and the additional conditions
Gaussian mixture models


L
1k
kk )(f)(f mm
),()( )()( k
m
k
mk Nf Σμm 
0,1 k
L
1k
k 
Example of 1D mixture with L=2
components (PDF and 500 random
sample histogram)

18. – 18
Gaussian mixture models
Gaussian Mixture distribution ),;(~ )()(
1
k
m
k
m
L
k
k N Σμmm 

Weights, means and covariance matrices estimated by EM method
(Hastie, Tibshirani, Friedman, The Elements of Statistical Learning, 2009)

19. – 19
• Linear inverse problem
Linear inverse problems (Gaussian)
),(~ mmN Σμm
εGmd 
),(~ dmdm
N Σμdm
),(~ Σ0ε N
NNMMN
RRRRR  εGmd and:,,
)()( 1
| m
T
m
T
mmdm GμdΣGGΣGΣμμ  

m
T
m
T
mmdm GμΣGGΣGΣΣΣ 1
| )( 
 
• If
then
Tarantola, Linear inverse problems, 2005.

20. – 20
Linear inverse problems (Gaussian)
• This result is based on two well known
properties of Gaussian distributions:
A. The linear transform of a Gaussian
distribution is again Gaussian;
B. If the joint distribution (m,d) is Gaussian,
then the conditional distribution m|d is
again Gaussian.
• These two properties can be extended to the
Gaussian Mixture case.

21. – 21
• Linear inverse problem
Linear inverse problems (GM)
εGmd 
),;()(~ )()(
1
k
dm
k
dm
L
k
k N Σμmddm 

),(~ Σ0ε N
NNMMN
RRRRR  εGmd and:,,
)()( )(1)()()()(
|
k
m
Tk
m
Tk
m
k
m
k
dm GμdΣGGΣGΣμμ  

)(1)()()()(
| )( k
m
Tk
m
Tk
m
k
m
k
dm GμΣGGΣGΣΣΣ 
 
• If
then
),;(~ )()(
1
k
m
k
m
L
k
k N Σμmm 

),;()(,
)(
)(
)(
1
k
d
k
dkL
j jj
kk
k Nf
f
f
Σμdd
d
d
d 
 



Analytical
expression

22. – 22
Introductory example
Reference Model: Trivariate distribution with 2 Tri-Normal
distributions (Gaussian mixture with 2 components)
)(f)(f)(f 2211 mmm 
),()( )1()1(
1 mmNf Σμm 











3
2
1
m
m
m
m
),()( )2()2(
2 mmNf Σμm 

23. – 23
Introductory example
First element distribution
Second element distribution Third element distribution

24. – 24
Introductory example
Transformed data (G linear forward model)







232221
131211
ggg
ggg
G 






2
1
d
d
d











3
2
1
m
m
m
m
εGmd 
),( Σ0ε N

25. – 25
Introductory example
Inverted Model with Bayesian traditional formulation
)()( 1
m
T
m
T
mmest GμdΣGGΣGΣμm  


26. – 26
Introductory example
Inverted Model with Bayesian GMM formulation
 )()( )(1)()()(
1
k
m
Tk
m
Tk
m
k
m
L
k
kest GμdΣGGΣGΣμm  

 

27. – 27
Introductory example
Comparison:
Reference model
Inverted - Bayesian GMM
Inverted - Bayesian Gaussian

28. – 28
Introductory example
Comparison:
Reference model
Inverted - Bayesian GMM
Inverted - Bayesian Gaussian

29. – 29
Inverse problem
Problem 1: We know the seismic amplitudes of
waves (measured data) and we want to
estimate elastic attributes.
Problem 2: We know the velocity of waves traveling
in the subsurface (from a model) and we
want to estimate rock properties;
Seismic data Porosity
SummaryInverse modeling in petroleum geophysics

30. – 30
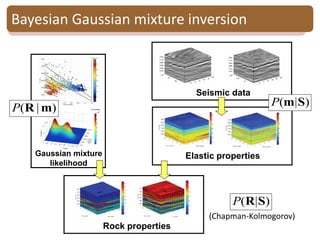
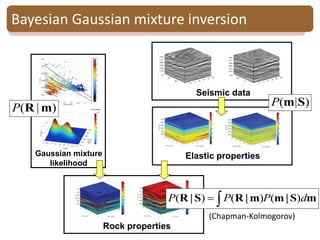
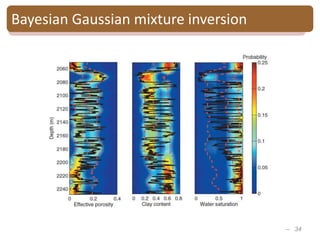
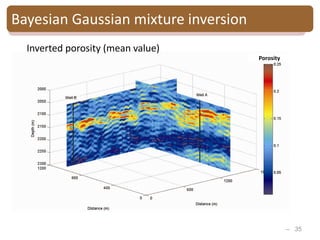
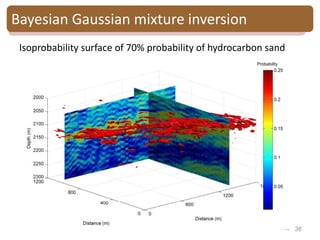
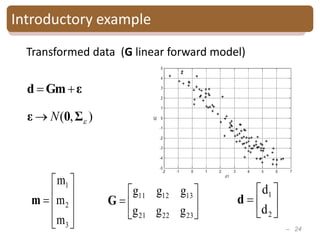
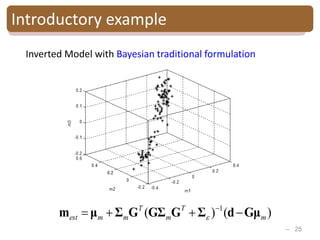
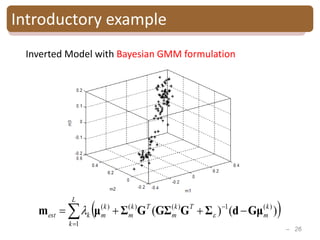
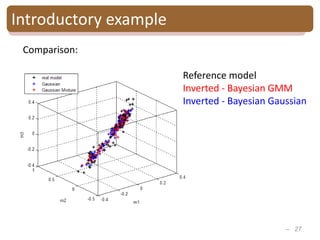
Bayesian Gaussian mixture inversion
• Goal: - Estimate reservoir properties R
from seismic data S
-Evaluate the model uncertainty
)](),(),([
],,[
)|(
321 

SSS
swc
P


S
R
SR
Porosity
Clay content
Water saturation
Partial-stack
seismic data
We estimate the posterior probability:

31. Bayesian Gaussian mixture inversion
• Seismic data S depend on reservoir
properties R through elastic properties m
• We can split the inverse problem into
two sub-problems:
•
• ff
gg
)(
)(
Rm
mS


))(( RS gf
seismic linearized modeling
rock physics model

32. Bayesian Gaussian mixture inversion
Elastic properties
Seismic data
)( Sm|P
Gaussian mixture
likelihood
)|( mRP
Rock properties
)( SR|P
(Chapman-Kolmogorov)

33. Bayesian Gaussian mixture inversion
Elastic properties
Seismic data
)( Sm|P
Gaussian mixture
likelihood
)|( mRP
Rock properties
mS|mm|RS|R dPPP )()()( 
(Chapman-Kolmogorov)

34. – 34
Bayesian Gaussian mixture inversion

35. – 35
Bayesian Gaussian mixture inversion
Inverted porosity (mean value)
Porosity

36. – 36
Bayesian Gaussian mixture inversion
Isoprobability surface of 70% probability of hydrocarbon sand
Probability

37. – 37
Time-lapse studies
• In time-lapse reservoir modeling we aim to
model reservoir property changes from
repeated seismic surveys.
Inverse problem
Time-lapse seismic data
Reservoir property changes
(saturation and pressure)

38. – 38
Bayesian time-lapse inversion
Gas saturation (2003) Gas saturation (2006)

39. – 39
Bayesian time-lapse inversion

40. – 40
Bayesian time-lapse inversion

41. – 41
Bayesian time-lapse inversion

42. Estimation vs Sampling: Geostatistics
• Estimated mean
• Geostatistical realization
– 42

43. – 43
Sequential simulations
• Sequential Gaussian Simulation (SGSim) is a specific case
of linear inverse problem with sequential approach
(the linear operator is the identity)
• The sequential approach to linear inverse problems
(Gaussian case) was proposed by Hansen et al. (2006)
• We extended this approach to Gaussian Mixture models

44. – 44
Sequential inversion (Gaussian)
mi
εGmd 
NNM
RRR  εG and:

45. – 45
Sequential inversion (Gaussian)
mi
εGmd 
NNM
RRR  εG and:
ms is the subvector of direct observations of m

46. Sequential inversion (Gaussian)
Hansen et al., Linear inverse Gaussian theory and geostatistics: Geophysics, 2006.
mi
εGmd 
NNM
RRR  εG and:
),;(~),( ),(),( dmdm
Σμmdm sisi mmsi Nm
),(~ Σ0ε NIf
then
),;(~ mmN Σμmm
ms is the subvector of direct observations of m

47. – 47
Sequential inversion (GM)
mi
εGmd 
NNM
RRR  εG and:
ms is the subvector of direct observations of m

48. – 48
Sequential inversion (GM)
Analytical formulation form means, covariance matrices, and weights.
mi
εGmd 
NNM
RRR  εG and:
),(~ Σ0ε NIf
then
ms is the subvector of direct observations of m
),;(~),( )(
),(
)(
),(
1
k
m
k
m
L
k
ksi sisi
Nm dmdm
Σμmdm 

),;(~ )()(
1
k
m
k
m
L
k
k N Σμmm 


49. – 49
SGMixSim: conditional simulations

50. – 50
Seq. Bayesian GM inversion: example 1

51. – 51
Seq. Bayesian GM inversion: example 2

52. Introduction to reservoir modeling
– 52– 52
The static reservoir model provides a ‘snapshot’ of the
reservoir before production starts.
When production starts, for example by water injection
or depletion, fluid saturation and fluid pressure change in
time.
Dynamic reservoir modeling (i.e. fluid flow simulation)
predicts hydrocarbon displacement and pressure changes
(by solving equations of fluid flow through porous media
based on finite volumes).

53. Introduction to reservoir modeling
– 53– 53
In dynamic reservoir model, we run fluid flow
simulations and obtain:
• Production forecast at the well locations
• Snapshot of saturation and pressure at different
time steps.

54. Introduction to reservoir modeling
– 54
Due to uncertainty in the data and approximations of the models,
reservoir model predictions are uncertain. After N years of
production, we can compare production data with predictions.
History matching is a data assimilation technique that allows
updating the model until it closely reproduces the past behavior
of a reservoir.

55. History matching
– 55
Problem: Find the most likely model of initial porosity and
permeability to match the measured production history of the
first N years of production.
Method: Bayesian updating

56. History matching
– 56
Method: Ensemble Kalman Filter (EnKF)
Injector
Producer
N porosity models
N production forecasts
Data
Simulations

57. Re-parameterization
– 57
Synthetic reservoir (modified from Panzeri et al., 2014, Ecmor
conference proceeding)
Log Permeability (true model) Water saturation after 3600 days

58. Re-parameterization
– 58
POD-DEIM response computed from 60 ‘snapshot’ of saturations
(i.e. saturation fields at 60 different times steps, every 60 days)
Example 1: 5 eigenvalues retained
DEIM point locations

59. Re-parameterization
– 59
Example 2: Similar example
with 20 eigenvalues.
The 20 DEIM points are
located along the channel. It
seems that the DEIM points
dynamically follow the water
front displacement.
Using the POD-DEIM
reduced model we can
reconstruct the true
production forecast

60. – 60
SummaryCurrent research projects
• Joint seismic-EM inversion • Seismic history matching (re-
parameterization of the water
front)

61. Conclusions
– 61– 61
Bayesian inverse methods are a powerful tool in reservoir
modeling for property estimation and uncertainty
quantification
The Gaussian mixture approach can be used for
multimodal models and preserve the analytical solution
The Bayesian approach can be extended to history
matching problems upon a re-parameterization of the
data assimilation problem

62. – 62
Acknowledgements
• Thanks to Erwan Gloaguen and INRS for the
invitation
• Thanks to IAMG to support UWyo and INRS
student chapters
• Thanks for your attention