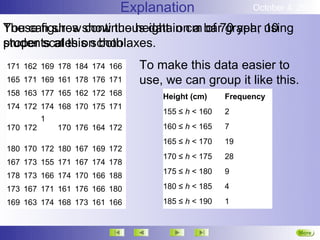
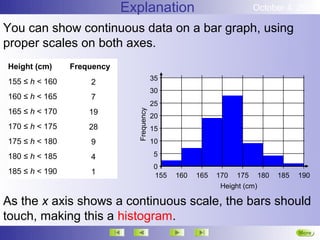
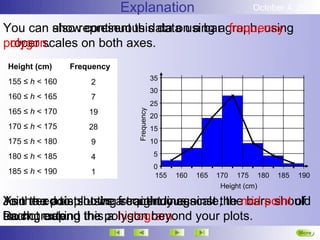
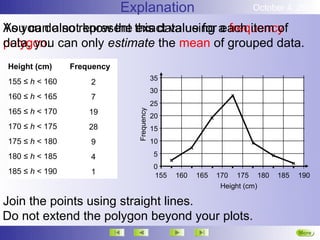
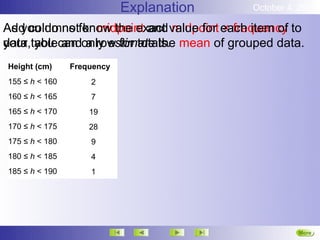
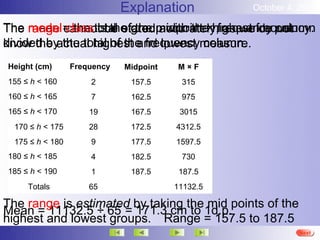
This document discusses representing and summarizing continuous data. Continuous data does not fit into categories but changes gradually, like height, weight, or temperature. When measuring continuous data, measurements are rounded and grouped at the level of accuracy used. Continuous data can be grouped into intervals and displayed using histograms or frequency polygons. The mean of grouped continuous data can be estimated using the midpoint of each interval multiplied by its frequency and dividing the total by the total frequencies.

1. October 4, 2012
Grouping Data
3. Representing continuous data.
Next

2. Explanation October 4, 2012
Sometimes data is continuous. That means it doesn't fit
into distinct categories, such as shoe size, but changes
gradually.
Height, weight, length, time and temperature are all
continuous. There is a continuous scale that can be
read at an infinite number of points.
If you record a measurement with a figure, such as
18 cm, it is unlikely that this is actually exact.
More
Next

3. Explanation October 4, 2012
This credit card card is about 8 cm long…
but if we look closer…
we can see that it is 8.2 cm long…
and if we look closer still…
we see that it is 8.2 cm, and a bit more.
More
Next

4. Explanation October 4, 2012
So when you make any measurement, you are probably
rounding it up or down, whether to a decimal place, or a
whole figure.
Even when you use decimal places, you are unlikely to
write an absolutely exact measurement.
You are in fact grouping the data at the level of accuracy
you choose to use.
When you say something is ‘18 cm’, you may mean…
‘any reading equal to, or more than
17.5 cm and less than 18.5 cm’.
More
Next

5. Explanation October 4, 2012
This can be written 17.5 ≤ w < 18.5
17.5 18.5
is more than, and less than
or equal to
The width of
‘any reading equal to,card
the credit or more than
17.5 cm and less than 18.5 cm’.
To make handling continuous data easier, it can be put
into groups larger than a single whole number.
More
Next

6. Explanation October 4, 2012
These figures show the height in cm bar70 year using
You can show continuous data on a of graph, 10
students at this school.
proper scales on both axes.
171 162 169 178 184 174 166 To make this data easier to
165 171 169 161 178 176 171 use, we can group it like this.
158 163 177 165 162 172 168 Height (cm) Frequency
174 172 174 168 170 175 171
155 ≤ h < 160 2
1
170 172 170 176 164 172 160 ≤ h < 165 7
165 ≤ h < 170 19
180 170 172 180 167 169 172
170 ≤ h < 175 28
167 173 155 171 167 174 178
175 ≤ h < 180 9
178 173 166 174 170 166 188
173 167 171 161 176 166 180 180 ≤ h < 185 4
169 163 174 168 173 161 166 185 ≤ h < 190 1
More
Next

7. Explanation October 4, 2012
You can show continuous data on a bar graph, using
proper scales on both axes.
Height (cm) Frequency
35
155 ≤ h < 160 2
30
160 ≤ h < 165 7
25
165 ≤ h < 170 19
Frequency
20
170 ≤ h < 175 28 15
175 ≤ h < 180 9 10
180 ≤ h < 185 4 5
0
185 ≤ h < 190 1 155 160 165 170 175 180 185 190
Height (cm)
As the x axis shows a continuous scale, the bars should
touch, making this a histogram.
More

8. Explanation October 4, 2012
You can show continuous data on a bar graph, using
also represent this data using a frequency
polygon.
proper scales on both axes.
Height (cm) Frequency
35
155 ≤ h < 160 2
30
160 ≤ h < 165 7
25
165 ≤ h < 170 19
Frequency
20
170 ≤ h < 175 28 15
175 ≤ h < 180 9 10
180 ≤ h < 185 4 5
0
185 ≤ h < 190 1 155 160 165 170 175 180 185 190
Height (cm)
Join need to plot the a continuous scale, themid point of
You the axis shows straight lines.
As the x points using frequency against the bars should
Do not making the polygon beyond your plots.
each group.
touch, extend this a histogram.
More

9. Explanation October 4, 2012
As you do not know the exact value for each item of
You can also represent this data using a frequency
data, you
polygon. can only estimate the mean of grouped data.
Height (cm) Frequency
35
155 ≤ h < 160 2
30
160 ≤ h < 165 7
25
165 ≤ h < 170 19
Frequency
20
170 ≤ h < 175 28 15
175 ≤ h < 180 9 10
180 ≤ h < 185 4 5
0
185 ≤ h < 190 1 155 160 165 170 175 180 185 190
Height (cm)
Join the points using straight lines.
Do not extend the polygon beyond your plots.
More

10. Explanation October 4, 2012
As you do not know the exact midpoint × frequency
Add columns for midpoint and value for each item of to
data, you and a row for totals.
your tablecan only estimate the mean of grouped data.
Height (cm) Frequency
155 ≤ h < 160 2
160 ≤ h < 165 7
165 ≤ h < 170 19
170 ≤ h < 175 28
175 ≤ h < 180 9
180 ≤ h < 185 4
185 ≤ h < 190 1
More

11. Explanation October 4, 2012
Add mean = the total of the midpoint × frequency column
The columns for midpoint and midpoint × frequency to
your table and total offor totals.
divided by the a row the frequency column.
Height (cm) Frequency Midpoint M×F
155 ≤ h < 160 2 157.5 315
160 ≤ h < 165 7 162.5 975
165 ≤ h < 170 19 167.5 3015
170 ≤ h < 175 28 172.5 4312.5
175 ≤ h < 180 9 177.5 1597.5
180 ≤ h < 185 4 182.5 730
185 ≤ h < 190 1 187.5 187.5
Totals 65 11132.5
Mean = 11132.5 ÷ 65 = 171.3 cm to 1d.p.
More

12. Explanation October 4, 2012
The mean = the total ofgroup with the×highest frequency.
modal cannot be statedmidpoint frequency column
range class is the the accurately, as we do not
divided by the total of the frequencymeasure.
know the actual highest and lowest column.
Height (cm) Frequency Midpoint M×F
155 ≤ h < 160 2 157.5 315
160 ≤ h < 165 7 162.5 975
165 ≤ h < 170 19 167.5 3015
170 ≤ h < 175 28 172.5 4312.5
175 ≤ h < 180 9 177.5 1597.5
180 ≤ h < 185 4 182.5 730
185 ≤ h < 190 1 187.5 187.5
Totals 65 11132.5
The range is estimated by taking the mid points of the
Mean = 11132.5 ÷ 65 = 171.3 cm to 1d.p.
highest and lowest groups. Range = 157.5 to 187.5
More
Next
End