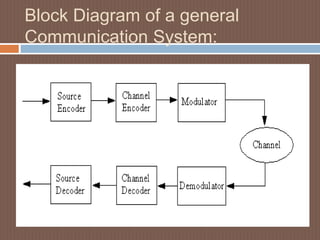
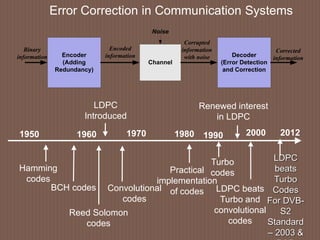
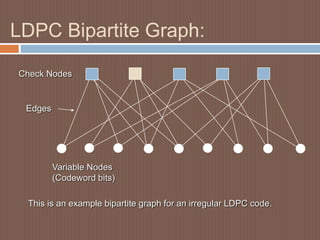
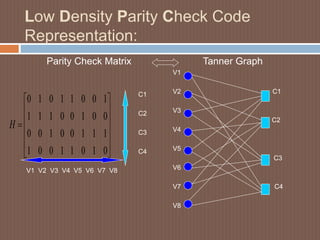
This document discusses low-density parity-check (LDPC) codes. It begins with an overview of LDPC codes, noting they were originally invented in the 1960s but gained renewed interest after turbo codes. It then covers LDPC code performance and construction, including generator and parity check matrices. Various representations of LDPC codes are examined, such as matrix and graphical representations using Tanner graphs. Applications of LDPC codes include wireless, wired, and optical communications. In conclusions, turbo codes achieved theoretical limits with a small gap and led to new codes like LDPC codes, which provide high-speed and high-throughput performance close to the Shannon limit.

1. Sri Prakash College of Engineering, Affliated to
JNTU-K
Rajupeta, Tuni.
Dept of Electronics & Communication Engineering.

2. REVIEW
Design & implementation of
Synthesizable LDPC
Venkatesh Pulugurtha

3. LDPC codes have been discovered a long time ago & re-
discovered after invention of turbo codes. These two codes
are actors of revolution of error correcting codes theory.
In this thesis, the principle of LDPC codes will be studied.
Besides, based on this, design is done for the IP core,
involves
LDPC code performance and construction of behavioural
model for Encoder & Decoder using Generator matrix and
parity check matrix , then use Modelsim for compilation &
Abstract:

4. Block Diagram of a general
Communication System:

5. Error Correction in Communication Systems
Encoder
(Adding
Redundancy)
Channel
Decoder
(Error Detection
and Correction
Noise
Binary
information
Corrected
information
Encoded
information
Corrupted
information
with noise
Reed Solomon
codes
Hamming
codes
LDPC
Introduced
Convolutional
codes
BCH codes
Renewed interest
in LDPC
Turbo
codes
19701960 1990 20001980
Practical
implementation
of codes LDPC beats
Turbo and
convolutional
codes
LDPC
beats
Turbo
Codes
For DVB-
S2
Standard
– 2003 &
2012

6. What is Coding?
 Coding is the conversion of information to another
form for some purpose.
 Source Coding : purpose is lowering redundancy
in information.
 Channel Coding : purpose is to defeat channel
noise.
 Channel Encoding: Application of Redundant
symbols to correct data errors.
 Modulation: conversion of symbols to a waveform
for transmission.
 Demodulation: conversion of waveform back to
symbols usually one at a time.
 Encoding:chooses message codeword &
transmits across the channel.

7. Types of codes:
 Linear codes : it can
be represented
(n,k). Its main
feature is does not
depends up on past
message.
 Convolution codes:
it can be
represented (n,k,m).
Its main feature is
depends up on past
message .

8. Low-Density Parity-Check
Codes:
Turbo and LDPC Codes
 Low-Density Parity-Check (LDPC) codes are a class of linear
block codes characterized by sparse parity check matrices H
 H has a low-density of 1’s
 LDPC codes were originally invented by Robert Gallager in the
early 1960’s but were largely ignored until they were “rediscovered”
in the mid-1990’s by MacKay
 Sparseness of H can yield large minimum distance dmin and
reduces decoding complexity
 Can perform within 0.0045 dB of Shannon limit

9. Low Density Parity Check Codes:
0521  ccc
0641  ccc
06321  cccc
Consider the 6 bit long codeword in the form
which satisfies 3 parity check equations as shown below.
 654321 ,,,,, ccccccc 
We can now define 3x6 parity check matrix as,











100111
101001
010011
H
521 ccc 
The density of ‘1’s in LDPC code parity check matrix is very low
Column weight - number of ‘1’s in a column
Number of times a symbol taking part in parity checks
 cw
Row weight - number of ‘1’s in a row Number of
Number of symbols taking part in a parity check
 cw
If the parity check matrix has uniform row weight and uniform column weight (same number of ‘1’ in a
column and same number of ‘1’ in a row) we call that a regular parity check matrix.
and changes, therefore this is an irregular
parity check matrix
rw cw

10. Represntation of LDPC Codes:
 Matrix representation of LDPC Codes:
 If H is a parity check matrix,with order of
(nxm),where n-No of columns,m-no of rows.
 Graphical representation of LDPC Codes:
 Tanner introduced graphical representation for
LDPC codes,also called as Bipartite graphs
helps to describe the decoding Algorithm.
 In graphical representation ,tanner graphs
provides a complete representation of the
code.

11. Graphical Representation:-
Tanner Graphs:-
 A Tanner graph is a bipartite graph that describes the parity check
matrix H
 There are two classes of nodes:
 Variable-nodes: Correspond to bits of the codeword or equivalently, to
columns of the parity check matrix
 There are n v-nodes
 Check-nodes: Correspond to parity check equations or equivalently, to
rows of the parity check matrix
 There are m=n-k c-nodes
 Bipartite means that nodes of the same type cannot be connected (e.g.
a c-node cannot be connected to another c-node)
 The ith check node is connected to the jth variable node iff the (i,j)th
element of the parity check matrix is one, i.e. if hij =1
 All of the v-nodes connected to a particular c-node must sum (modulo-2)
to zero

12. LDPC Bipartite Graph:
This is an example bipartite graph for an irregular LDPC code.
Check Nodes
Edges
Variable Nodes
(Codeword bits)

13. Low Density Parity Check Code
Representation:
Parity Check Matrix
C1
C2
C3
C4
V1 V2 V3 V4 V5 V6 V7 V8
Tanner Graph
V1
V2 C1
V3
C2
V4
V5
C3
V6
V7 C4
V8













0101
1110
0010
1001
1001
0100
0111
1010
H

14. •A binary parity check code is a block code: i.e., a
collection of binary vectors of fixed length n.
•The symbols in the code satisfy r parity check
equations of the form:
where Ex-or means modulo 2 addition and
xa , xb , xc,… ,xz
are the code symbols in the equation.
•Each codeword of length n can contain (n-r)=k
information digits and r check digits.
The percentage of 1s in the parity check matrix for a
LDPC code is low
 WHAT IS PARITY CHECK MATRIX &
PARITY CHECK CODE?

15. Parity check matrix & Low density
condition:
 -Defining the two(2) numbers describing parity
check matrix H.
 Wr- No of 1’s in a row;Wc-No of 1 s in a column.
 Low Density Conditions:
 Wc<<n & Wr<<m; where n-No of columns & m-No
of rows of a parity check matrix with a order of
(nxm) are the two conditions of a (n,m) code or H-
matrix to satisfy the low density condition.
 Parity check matrix is indicated by H, consists of
elements 1s & 0s represented by Hij,where i&j are
positional elements of rows and columns.

16. Regular & Irregular LDPC’S:
 Regular LDPC codes: A LDPC code is regular
only if Wc (No of 1s in a column) is constant
for every column then Wr = Wc x (n/m) is also
constant for every row i.e.., Wr=2(8/4)=4,it
represents no of 1s in a row i.e., Wr=4 & Wc=2
that are of constant values for every column &
every row of H matrix need to be regular.
 Irregular LDPC codes: Even if H is low
density,but the no of 1s in each row or column
are not constant,then the LDPC code is said to
be irregular.

17. Code Design for LDPC Codes:
 To achieve good coding gain performance, good
LDPC code design is essential.
 A code design based on density evolution is
only 0.0045dB away from the Shannon bound.
However, it’s a rate-1/2 irregular code with
maximum variable degree of 100 and blokc size
of 107bits. It also requires an average of more
than 1000 iterations to achieve the result.

18. Decoding LDPC codes:
 Like Turbo codes, LDPC can be decoded iteratively
– Instead of a trellis, the decoding takes place on a Tanner graph
– Messages are exchanged between the v-nodes and c-nodes
– Edges of the graph act as information pathways
 Hard decision decoding:
– Bit-flipping algorithm(BFA)
 Soft decision decoding:
– Sum-product algorithm
• Also known as message passing/ Belief Propagation Algorithm(BPA)
– Min-sum algorithm
• Reduced complexity approximation to the Sum-Product Algorithm(SPA)
 In general, the per-iteration complexity of LDPC codes is less than it is
for turbo codes

19. Turbo Code Performance
Example:

20. LDPC Code Performance
Example:
]
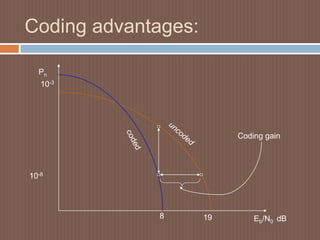
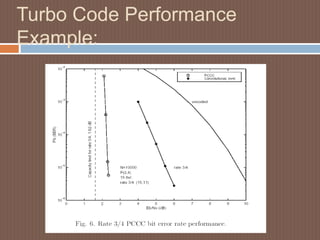
LDPC Performance can
Be very close to capacity.
The closest performance
To the theoretical limit
ever was with an LDPC,
and within 0.0045dB of
capacity.
The code shown here is
a high-rate code and
is operating within a few
tenths of a dB of capacity.
Turbo Codes tend to work
best at low code rates and
not so well at high code
rates.
LDPCs work very well at
high

21. Coding advantages:
Pn
Eb/N0 dB
10-8
10-3
8 19
Coding gain

22. Coding disadvantages:
 More bandwidth due to redundant
 Processing Delay
 Design Complexity

23. Applications of LDPC Codes:
 Wireless, Wired, and Optical Communications.
 Different throughput requirement
 Need to design codes that work with multi-
level modulation (e.g. QAM or M-PSK)
 Satellite communications

24. Conclusions :
 Turbo codes achieved the theorical limits with
small gap
 Give rise to new codes : Low Density Parity
Check (LDPC)
 LDPC S are of high speed,high
throughput,good performance.
 Need:-
 Improvements in decoding delay