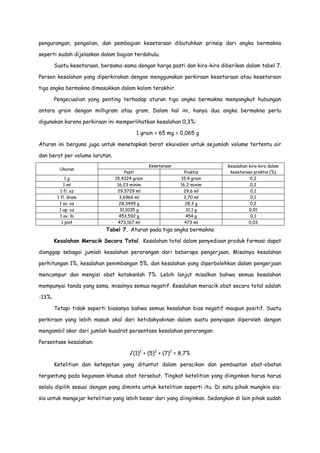
Dokumen ini menjelaskan pentingnya pemahaman dasar-dasar fisika dan matematika dalam bidang farmasi, termasuk penerapan prinsip-prinsip tersebut dalam praktik farmasi sehari-hari. Ahli farmasi dituntut untuk menguasai pengukuran dan satuan, serta menerapkan konsep ilmiah untuk memecahkan persoalan praktis. Struktur dan pembahasan mengenai dimensi, satuan, gaya, energi, dan penggunaan komputer dalam farmasi juga diuraikan dalam dokumen ini.

1. Tugas Rangkuman
DASAR-DASAR FISIKA DAN MATEMATIKA
“FARMASI FISIKA”
O
L
E
H
Nama
: Abulkhair Abdullah
NIM
: 70100111001
Kelas
: Farmasi A1
Jurusan Farmasi
Fakultas Ilmu Kesehatan
Universitas Islam Negeri Alauddin Makassar
SAMATA-GOWA
2012

2. DASAR-DASAR FISIKA DAN MATEMATIKA
Sekarang ini, seorang ahli farmasi dituntut untuk menunjukkan pengetahuannya dalam
bidang farmakologi, kimia organik, biokimia, dan pengertian ilmiah mengenai sifat-sifat fisika dan
kimia dari poduk obat baru yang ia buat dan edarkan.
Walaupun terikat dalam kegiatan penelitian, mengajar, industri, apotek, atau kegiatan lain
yang berhubungan dengan profesinya, ahli farmasi harus menyadari akan pentingnya penerapan
ilmu-ilmu dasar.
Prinsip ilmiah dari farmasi tidak sesulit yang dikira, dan sesungguhnya tidak berada di luar
jangkauan pengertian dari ahli farmasi terdidik saat ini.
Nama farmasi fisik telah diasosiasikan dengan bidang farmasi yang menggeluti prinsipprinsip ilmu penjumlahan dan teoretis karena mereka menggunakannya untuk farmasi praktis.
Farmasi fisik mencoba mempersatukan pengetahuan fakta farmasi melalui pengembangan prinsipprinsipnya yang luas dan hal ini membantu ahli farmasi, ahli farmakologi, dan ahli kimia farmasi
dalam usahanya untuk meramalkan kelarutan, kestabilan, tercampurnya obat, dan aksi biologi dari
obat.
KONSEP DAN METODE ILMU
Pelajaran ini harus menjadi titik balik dalam pola belajar mahasiswa tingkat lanjut karena
bagian terakhir dari kurikulum farmasi, titik beratnya terletak pada pemakaian prinsip ilmiah
untuk mempraktekkan problema keahlian. Mahasiswa harus berjuang dalam pelajaran ini untuk
menyatukan fakta dan buah pikiran menjadi satu kesimpulan yang berarti. Dalam karirnya yang
akan datang, kadang-kadang ia akan terpanggil untuk memecahkan persoalan farmasi praktis.
Pemahaman dari bahan kuliah merupakan tanggung jawab yang utama dari mahasiswa.
Setiap tugas hendaknya dibaca dan dibuat garis besarnya dan soal tugas hendaknya dipecahkan di
luar kelas. Komentar guru selanjutnya perlu untuk menjelaskan hal-hal yang kurang jelas dan
menolong murid untuk memperbaiki pendapatnya dan kemampuannya memberi alasan.
DIMENSI DAN SATUAN
Sifat dari suatu zat biasanya dinyatakan dengan kegunaan dari ketiga besaran yang dipilih,
yaitu panjang, massa, dan waktu. Setiap sifat ini dinyatakan oleh satu satuan tertentu dan
rujukan baku. Dalam system metrik, satuannya adalah sentimeter (cm), gram (g), dan detik (sec).

3. Besaran yang dapat diukur seperti luas, kerapatan, tekanan, dan energi disatukan dari
ketiga sifat dasar tadi. Jadi besaran panjang, luas, dan volume diukur dalam dimensi panjang (L),
panjang kuadrat (L2), dan panjang kubik (L3), bersesuaian dengan satuan cm, cm2, dan cm3.
Dimensi dan satuan dasar diperlihatkan dalam tabel 1.
Besaran yang dapat
diukur
Panjang (l)
Massa (m)
Waktu (t)
Lambing dimensi
Satuan cgs
Satuan SI
Rujukan baku
L
M
T
Sentimeter (cm)
Gram (g)
Detk (s)
Meter (m)
Kilogram (kg)
Detik (s)
Meter
Kilogram
Rata-rata matahari
Tabel 1. Dimensi dan satuan dasar
The International Union of Pure and Applied Chemistry (IUPAC) telah memperkenalkan
suatu Sistem Internasional (SI) dalam usaha untuk menetapkan suatu satuan internasional yang
seragam. Farmasi fisik pada umumnya memakai satuan cgs atau sistem satuan yang umum.
Panjang dan Luas. Dimensi panjang berlaku sebagai pengukur jarak dan mempunyai rujukan
baku meter. Hal ini didefinisikan sebagai berikut:
1 meter = 1,65076373 x 106
di mana
Kr-86
Kr-86
= 6,0578021 x 10-7 m adalah panjang gelombang dalam kekosongan transisi antara
dua tingkat energi spesifik dari atom kripton-86.
Pengali
1012
109
106
103
10-3
10-6
10-9
10-12
Awalan
Tera
Giga
Mega
Kilo
Mili
Mikro
Nano
Piko
Simbol
T
G
M
k
m
µ
n
p
Tabel 2. Pembagian dan pengalian satuan
Volume. Besaran yang dapat diukur. Volume juga diturunkan dari panjang. Rujukan bakunya
adalah meter kubik. Volume didefinisikan dalam bentuk liter, yaitu volume dari satu kilogram air
pada tekanan 1 atmosfer da 4oC dan berarti setara dengan 1000 cm3.
Massa. Standar dari massa adalah kilogram. Satuan praktis dari massa dalam sistem cgs
adalah gram (g), yaitu seperseribu dari satu kilogram. Massa sering dinyatakan sebagai berat
dari suatu benda.
Kerapatan dan Berat Jenis. Kerapatan adalah turunan besaran karena menyangkut satuan
massa dan volume. Batasannya adalah massa persatuan volume pada temperatur dan tekanan
tertentu dan dinyatakan dalam sistem cgs dalam gram per sentimeter kubik (g/cm 3).
Berbeda dengan kerapatan, berat jenis adalah bilangan murni tanpa dimensi yang dapat
diubah menjadi kerapatan dengan menggunakan rumus yang cocok. Berat jenis didefinisikan

4. sebagai perbandingan kerapatan dari suatu zat terhadap kerapatan air, harga kedua zat itu
ditentukan pada temperatur yang sama, jika tidak dengan cara lain yang khusus.
Besaran yang diukur
Dimensi
Satuan cgs
Satuan SI
Luas (A)
Volume (V)
L2
L3
cm2
cm3
m2
m3
Kerapatan (ρ)
ML-3
g/cm3
kg m-3
Kecepatan (v)
LT-1
cm/dt
ms-2
Percepatan (a)
LT-2
cm/dt2
ms-2
Gaya (f)
MLT-2
g cm/dt2 atau dyne
Tekanan (p)
ML-1T-2
dyne/cm2
Energi (E)
ML2T-2
g cm2/dt2 atau erg
kg ms-2 atau Jm-1
atau N
Nm-2 atau kg m-1 s-2
atau Pa
kg m2 s-2 atau Nm
atau J
Hubungan dengan
dimensi lain
Panjang kuadrat
Panjang kubik
Massa per satuan
volume
Panjang per satuan
waktu
Panjang per waktu
kuadrat
Massa kali
percepatan
Gaya per satuan luas
Gaya kali panjang
-2
N singkatan dari newton, atau kilogram x meter x detik .
Pa singkatan dari pascal, atau newton x meter-2.
J lambing dari joule. Dalam tebel ini, m simbol dari meter, bukan massa.
L singkatan dari panjang, T untuk waktu, M untuk massa.
Tabel 3. Turunan dimensi dan satuan
Gaya. Makin besar massa tubuh dan makin besar percepatan yang dibutuhkan, makin besar
pula gaya yang harus dipunyai seseorang. Oleh karena itu, gaya berbanding langsung dengan massa
(jika percepatan konstan) dan percepatan (jika massa konstan). Ini dapat diperhatikan dengan
hubungan:
Gaya α Massa x Percepatan
(1)
sesuai dengan aljabar, dengan pemasukan harga konstan (tetapan). Sesuai dengan:
f=kxmxa
(2)
di mana f adalah gaya, k adalah tetapan perbandingan, m adalah massa, dan a adalah percepatan.
Jika satuan dipilih menjadi 1, maka persamaan gaya yang umum dikenal menjadi:
f=mxa
(3)
Hubungan antara berat dan massa dapat diperoleh dari persamaan (3). Masukkan berat (w) untuk
gaya dan g untuk percepatan, persamaan menjadi:
w=mxg
(4)
Kerja dan Energi. Energi seringkali didefinisikan sebagai keadaan yang dapat memberikan
kemampuan kepada benda untuk mengerjakan suatu pekerjaan. Energi dapat digolongkan pada
energi kinetik atau energi potensial.

5. Hasil kali gaya dengan jarak mempunyai dimensi yang sama dengan energi, yaitu ML 2T-2.
Hasil kali lain juga mempunyai dimensi energi adalah tekanan x volume, tegangan permukaan x
luas, massa x kecepatan2, dan beda potensial listrik x muatan listrik.
Satuan kerja dalam cgs juga satuan energi kinetik dan potensial adalah erg. Erg
didefinisikan sebagai kerja yang dilakukan jika gaya sebesar 1 dyne bekerja melalui jarak 1
sentimeter.
1 erg = 1 dyne x 1 cm
Erg kadang-kadang terlalu kecil untuk penggunaan praktis dan diganti joule (J = jewel) yang sama
dengan 107 erg:
1 joule = 1 x 107 erg
Dalam melakukan perhitungan dengan sistem cgs yang menyangkut kerja dan tekanan, kerja harus
dinyatakan dalam erg dan tekanan dalam dyne/cm 2. Jika menggunakan SI atau sistem lain, satuan
yang konsisten harus juga dipertahankan.
BEBERAPA UNSUR MATEMATIK
Perhitungan yang Menyangkut Dimensi. Pembagian dan perbandingan sering dipakai dalam
ilmu fisika untuk mengubah satu sistem ke sistem yang lain. Perhitungan berikut ini
menggambarkan kegunaan perbandingan.
Contoh 1. Berapa gram kalori terdapat dalam 3,00 joule? Orang pertama-tama akan mengingat hubungan kalori
dan joule. Hubungan tersebut adalah 1 kal = 4,184 joule, berapa kalori terdapat dalam 3,00 joule? Perbandingan dipakai
dengan hati-hati untuk menyatakan setiap kuantitas dalam satuannya yang cocok. Untuk besaran yang tidak diketahui
dipakai bilangan X.
Metode kedua, didasarkan pada kebutuhan bahwa satuan seperti juga dimensi, harus sama
pada kedua ruas persamaan. Metode ini kadang-kadang lebih cocok daripada metode
perbandingannya.
Contoh 2. Berapa gallon setara dengan 2,0 liter? Ini perlu untuk menyusun suatu perbandingan dalam
memecahkan soal ini. Dalam metode yang menyangkut identitas besaran pada kedua ruas persamaan, besaran yang dicari,
X (gallon), diletakkan pada ruas kiri dan kesetaraannya, 2,0 liter, diletakkan pada ruas sebelah kanan. Ruas kanan
kemudian harus dikalikan dengan hubungan yang diketahui dalam bentuk pecahan, misalnya 1 pint per 473 ml untuk
mendapatkan satuan dalam gallon. Melalui cara ini didapt hasil dengan satuan yang cocok.

6. Pangkat. berbagai pengerjaan yang menyangkut pangkat yaitu angka di mana bilangan
dipangkatkan sebaiknya dengan mempelajari contoh yang tertera pada tabel 4.
a x a x a = a3
2
3
2+3
a xa =a
a2/a4 = a 2-4 = a-2 = 1/a2
5
a2/a2 = a2-2 = a0 = 1
=a
(a2)3 = a2 x a2 x a2 = a6
a1/2 = √a
(a/b)3 = a3/b3
a1/2 x a1/2 = a1/2+1/2 = a1 = a
5
2
5-2
a /a = a
3
a2/3 = (a2)1/3 = 3√a2
=a
a5/a4 = a5-4 = a1 = a
Tabel 4. Aturan mengenai pangkat
Logaritma. Kesamaan dari
103 = 1000
(5)
Dinyatakan dalam notasi logaritma seperti:
Log10 1000 = 3
(6)
Pangkat 3 di mana bilangan dasar 10 dipangkatkan menghasilkan 1000 dalam persamaan (5)
ditunjukkan juga oleh logaritma 1000. Bilangan 1000 dikenal sebagai antilogaritma dari bilangan
3. Secara umum, jika b dipangkatkan dengan angka x, menghasilkan angka a, maka logaritma
terhadap bilangan dasar b dari a adalah x:
bx = a
logb a = x
Seperti terlihat dalam tabel 5, bilangan dapat dikalikan dan dibagi dengan menambahkan
dan mengurangi pangkat. Karena logaritma adalah pangkat, maka mengikuti aturan yang sama.
Beberapa sifat logartima diambil sebagai contoh dengan ciri-ciri yang dikumpulkan dalam tabel 5.
Log ab = log a + log b
Log 1/a = log 1 – log a = -log a
Log a/b = log a – log b
Log a2 = loh a + log a = 2 log a
Log 1 = 0 jika 100 = 1
Log √4 = log a1/2 = ½ log
-2
Log a = -2 log a = 2 log 1/a
Tabel 5. Aturan logaritma
Variasi. Ilmuwan secara terus-menerus berusaha untuk menghubungkan gejala dan
menetapkan kesimpulan untuk menguatkan dan menafsirkan data percobaan. Beberapa rumus
terkenal yang menggambarkan prinsip variasi dapat dilihat pada tabel 6.
Penghitungan
Persamaan
Keliling lingkaran
Kerapatan
Jarak benda jatuh
C = πD
M = ρV
s = 1/2gt2
Penurunan titik beku
ΔTf = Kfm
Variable tergantung
(tak bebas)
Keliling, C
Massa, M
Jarak, s
Penurunan titik beku,
ΔTf
Variable bebas
Diameter, D
Volume, V
Waktu, t2
Molalitas, m
Tetapan
perbandingan
Π = 3,14159…
Kerapatan, ρ
Tetapan gravitasi, ½ g
Tetapan krioskopik,
Kf
Metode Grafik. Besarnya variabel bebas biasanya diukur sepanjang skala koordinat
horizontal yang disebut x. Variabel tidak bebas diukur sepanjang skala vertikal atau sumbu y.

7. Data diplot pada grafik dan garis halus digambarkan melalui titik-titik. Harga x dari setiap titik
disebut koordinat x atau absis. Harga y disebut koordinat y atau ordinat. Titik potong antara
sumbu x dan y disebut titik asal. Harga x dan y bias negatif bias juga posotif.
Hubungan paling sederhana antara dua variaebel di mana variabel mengandung pangkat
tidak lebih dari satu (persamaan pangkat pertama). Garis lurus atau hubungan garis dinyatakan
sebagai:
y = a + bx
di mana y variabel tidak bebas, x variabel bebas, dan a dan b adalah tetapan. Tetapan b adalah
kemiringan garis. Makin besar harga b, makin curam kemiringan. Kemiringan dapat positif atau
negatif tergantung pada apakah garis miring ke kanan atas atau ke kanan bawah. Jika b = 1, garis
membuat sudut 45o terhadap sumbu x (tangen 450 = 1), dan persamaan garis dapat ditulis
sebagai:
y=a+x
Jika b = 0, garis adalah horizontal yaitu sejajar dengan sumbu x dan persamaannya:
y=a
Jika a positif, garis sumbu y di atas sumbu x. Jika negatif, dia memotong sumbu y di bawah
sumbu x. Jika a adalah 0, persamaan dapat ditulis dan garis melalui titik asal.
y = bx
Persamaan garis dapat diperoleh dengan menggunakan bentuk persamaan garis dengan dua
titik.
Dapat juga dilihat bahwa:
Komputer dan Kalkulator. Komputer dapat dibagi dalam mesin analog dan mesin digital.
Komputer digital memakai angka-angka seperti juga komputer mikro dan komputer yang dapat
digenggam. Kalkulator modern dilengkapi dengan pencatat untuk penyimpanan data dan sebuah
pusat yang dapat memprogram perintah matematik untuk menyelesaikan fungsi matematis.
Berbeda dengan komputer digital, komputer analog menangani problem matematis dengan
menggunakan voltase untuk memperlihatkan variaebl seperti konsentrais, tekanan, waktu, dan
temperatur. Komputer analog terdir dari puluhan atau ratusan amplifier yang digunakan untuk
pengerjaan matematis seperti penjumlahan, perkalian, dan sebagainya. Komputer analog
digunakan dalam teknik untuk merangsang aksi lompatan pada poros dari mobil atau pergerakan
dari pencakar langit pada angin kencang. Juga telah digunakan untuk menghitung absorpsi,

8. distribusi, dan tetapan eliminasi untuk obat yang diberikan pada pasien dan meplot kurva untuk
data pengambilan obat dan ekskresi. Sekarang ini komputer digital dapat juga menghitung hargaharga seperti itu dan menyiapkan grafik dengan fasilitasnya, dan popularitas dari komputer
analog dalam dunia farmasi telah berkurang akhir-akhir ini.
Angka Bermakna. Suatu angka bermakna adalah setiap angka yang digunakan untuk
menyatakan harga atau besaran pada tempat di mana ia berada. Bilangan nol dianggap sebagao
angka bermakna kecuali jika digunakan semata-mata untuk menempatkan titik desimal. Dua nol
yang dengan segera mengikuti titik desimal dalam bilangan 0,00750 hanya menempatkan titik
desimal dan tidak bermakna. Tetapi angka 0 setelah angka 5 bermaksa karena tidak diperlukan
untuk menulias angka tersebut. Jika tidak bermakna, dapat dihilangkan.
Angka bermakna dari suatu bilangan termasuk semua angka ditambah angka pertama yang
tidak berpengaruh. Angka bermakna dari beberapa harga diperlihatkan dalam tabel 6.
Bilangan
53
530,0
0,00053
5,0030
5,3 x 10-2
5,30 x 10-2
53000
Jumlah gambaran yang berarti
2
4
2
5
2
3
Tidak tertentu
Tabel 6. Gambaran yang bermakna
Dalam mengerjakan data percobaan, ada aturan-aturan tertentu untuk angka yang masuk
dalam perhitungan:
1.
Dalam menolak angka yang tidak berguna, naikkan dengan satu angka terakhir yang
dipertahankan jika angka yang ditolak berikutnya adalah 5 atau lebih besar dari 5.
Jangan mengubah angka terakhir jika angka yang ditolak mempunyai nilai yang lebih
kecil dari 5. Jadi angka 13,2764 dibulatkan menjadi 13,28. Harga 13,2744 dibulatkan
menjadi 13,27.
2.
Dalam penambahan atau pengurangan, hanya dimasukkan angka yang terkcil di belakang
koma dari bilangan-bilangan yang akan dikurangkan atau ditambahkan. Jadi dalam
menjumlahkan 442,75, 58,4, dan 2,680, bulatkan harga-harga ini sehingga mempunyai
satu angka di belakang koma menjadi 442,8 + 58,4 + 2,7 = 503,9.
3.
Dalam pengalian atau pembagian, aturan umum yang digunakan adalah untuk
mempertahankan bilangan yang sama dari angka bermakna pada hasil seperti muncul
dalam harga dengan bilangan terkecil dari angka bermakna. Dalam mengalikan 2,67 dan
3,2, hasil yang dicatat adalah 8,5 dan bukan 8,544.

9. 4.
Dalam menggunakan logaritma untuk mengalikan dan membagi, pertahankanlah bilangan
yang sama dari angka bermakna dalam mantissa seperti dalam bilangan aslinya.
5.
Jika hasil ini untuk digunakan dalam perhitungan lebih lanjut, pertahankanlah
setidaknya satu angka lebih daripada yang diusulkan pada aturan di atas. Hasil akhir
kemudian dibulatkan ke angka terakhir yang bermakna.
Kepekaan. Ketepatan dan ketelitian harus dikorbankan jika pekerja berusaha menimbang
dalam jumlah yang sangat kecil pada timbangan. Untuk menentukan jumlah terkecil dari zat yang
dapat ditimbang yaitu jumlah minimum yang masih diperbolehkan, seorang ahli farmasi harus
menetapkan kepekaan dari timbangan.
Kepekaan ditentukan dengan mengatur timbangan pada keseimbangan, tambahkan berat
katakanlah 20 mg) pada piring sebelah kanan dan amati penyimpangan dari penunjuk pada indeks
skala. Titik keseimbangan dari penunjuk tanpa berat dan dengan berat 20 mg pada piring dapat
ditentukan dengan cara yang biasa digunakan dalam analisis kuantitatif.
Contoh 3. Misalkan penunjuk timbangan istirahat pada angka 0 tanpa berat dan penyimpangan 2,5 bagian skala
mengikuti penambahan berat 20 mg. berapakah kepekaan timbangan?
20 mg ≈ 2,5 penyimpangan bagian skala
oleh karena itu
Kemungkinan lain, soal ini dapat diselesaikan sebagai berikut:
Contoh 4. Jika kepekaan timbangan 3 mg, berapakah jumlah minimum yang boleh ditimbang pada timbangan
tersebut? Timbangan dapat dipakai untuk menimbang dengan kesalahan ± 3 mg, menyatakan kesalahan relative tidak lebih
besar dari ± 5%. Kemudian berat minimum yang diperbolehkan didapat sebagai berikut:
Contoh 5. Hitunglah % kesalahan dalam penimbangan 200 mg pada timbangan dengan kepekaan 6 mg. kesalahan
tersebut dapat dihitung dengan menggunakan persamaan:
karena itu
Massa dan Kesetaraan Volume. Suatu kesimpulan yang didasarkan pada criteria ini
diajukan dan ditunjukkan di sini sebagai aturan tiga angka bermakna. Untuk penambahan,

10. pengurangan, pengalian, dan pembagian kesetaraan dibutuhkan prinsip dari angka bermakna
seperti sudah dijelaskan dalam bagian terdahulu.
Suatu kesetaraan, bersama-sama dengan harga pasti dan kira-kira diberikan dalam tabel 7.
Persen kesalahan yang diperkirakan dengan menggunakan perkiraan kesetaraan atau kesetaraan
tiga angka bermakna dimasukkan dalam kolom terakhir.
Pengecualian yang penting terhadap aturan tiga angka bermakna menyangkut hubungan
antara grain dengan milligram atau gram. Dalam hal ini, hanya dua angka bermakna perlu
digunakan karena perkiraan ini memperlihatkan kesalahan 0,3%:
1 grain = 65 mg = 0,065 g
Aturan ini berguna juga untuk menetapkan berat ekuivalen untuk sejumlah volume tertentu air
dan berat per volume larutan.
Ukuran
1g
1 ml
1 fl. oz
1 fl. dram
1 av. oz
1 ap. oz
1 av. lb
1 pint
Kesetaraan
Pasti
15,4324 grain
16,23 minim
29,5729 ml
3,6966 ml
28,3495 g
31,1035 g
453,592 g
473,167 ml
Praktis
15,4 grain
16,2 minim
29,6 ml
3,70 ml
28,3 g
31,1 g
454 g
473 ml
Kesalahan kira-kira dalam
kesetaraan praktis (%)
0,2
0,2
0,1
0,1
0,2
0,01
0,1
0,03
Tabel 7. Aturan pada tiga angka bermakna
Kesalahan Meracik Secara Total. Kesalahan total dalam penyediaan produk farmasi dapat
dianggap sebagai jumlah kesalahan perorangan dari beberapa pengerjaan. Misalnya kesalahan
perhitungan 1%, kesalahan penimbangan 5%, dan kesalahan yang diperbolehkan dalam pengerjaan
mencampur dan mengisi obat katakanlah 7%. Lebih lanjut misalkan bahwa semua kesalahan
mempunyai tanda yang sama, misalnya semua negatif. Kesalahan meracik obat secara total adalah
-13%.
Tetapi tidak seperti biasanya bahwa semua kesalahan bias negatif maupun positif. Suatu
perkiraan yang lebih masuk akal dari ketidakyakinan dalam suatu penyiapan diperoleh dengan
mengambil akar dari jumlah kuadrat persentase kesalahan perorangan:
Persentase kesalahan:
√(1)2 + (5)2 + (7)2 = 8,7%
Ketelitian dan ketepatan yang dituntut dalam peracikan dan pembuatan obat-obatan
tergantung pada kegunaan khusus obat tersebut. Tingkat ketelitian yang diinginkan harus harus
selalu dipilih sesuai dengan yang diminta untuk ketelitian seperti itu. Di satu pihak mungkin siasia untuk mengejar ketelitian yang lebih besar dari yang diinginkan. Sedangkan di lain pihak sudah

11. sepantasnya ahli farmasi mencapai ketepatan dan ketelitian yang cukup untuk menghasilkan
keamanan yang dapat dipertanggungjawabkan dan produk yang efektif.
METODE STATISTIK DAN ANALISIS KESALAHAN
Kesalahan dapat didefinisikan sebagai penyimpangan dari nilai mutlak atau dari rata-rata
sebenarnya dari sejumlah besar hasil. Ada dua tipe kesalahan yang dikenal yaitu konstan
(determinat) dan acak/kebetulan (indeterminat).
Kesalahan Deteminat. Kesalahan determinat atau konstan adalah kesalahan yang walaupun
kadang-kadang tidak diduga, dapat dihindarkan atau ditentukan dan diperbaiki begitu kesalahan
tersebut diketahui. Contoh kesalahan determinat adalah segala yang bersangkutan dengan
metode yang terutama dipakai, kesalahan dalam kalibrasi dan pengerjaan dari alat pengukuran,
ketidakmurnian dalam reagen dan obat, kesalahan perorangan yang disangka, sebagai contoh
kesalahan pembacaan meniscus yang berulang-ulang, kesalahan dalam penimbangan, dalam memadu
warna, dan dalam membuat perhitungan.
Kesalahan determinat dapat dihilangkan dengan kalibrasi alat timbang dan alat lain dengan
memeriksa perhitungan dan hasil oleh pekerja lain.
Kesalahan Indeterminat. Kesalahan terjadi tidak disengaja atau secara kebetulan dan
bervariasi dari satu pengukuran ke pengukuran berikutnya. Misalnya dalam suatu analisis kimia,
hasil satu rangkaian pengujian akan menghasilkan pola acak sekitar harga rata-rata atau nilai
uatma yang dikenal dengan mean. Kesalahan acak akan terjadi juga dalam mengisi sejumlah kapsul
dengan obat dan hasilnya akan memperlihatkan variasi berat tertentu.
Kesalahan indeterminat tidak dapat dibiarkan atau dikoreksi karena tidak sama pada setiap
pengukuran.
Ketepatan dan Ketelitian. Ketepatan adalah suatu ukuran kesepakatan di antara nilai-niali
dalam suatu kelompok data, sedangkan ketelitian adalah kesepakatan antara data dan nilai yang
benar. Kesalahan indeterminat mempengaruhi ketepatan hasil dan pengukuran ketapatan dicapai
paling baik dengan rata-rata statistik. Kesalahan determinat tetap mempengaruhi ketelitian data.
Teknik yang digunakan dalam menganalisis ketepatan hasil yang pada saatnya memberikan
pengukuran kesalahan indeterminat, akan ditetapkan mula-mula dan penemuan serta penghapusan
kesalahan determinat atau ketidaktelitian akan didiskusikan belakangan.
Kesalahan indeterminat mengkikuti teori kemungkinan, kesalahan positif dan negatif
kemungkinannya sama, dan kesalahan yang lebih besar sedikit memungkinkan daripada kesalahan
yang lebih kecil.