ATI's Radar Signal Analysis and Processing using MATLAB Technical Training Short Course Sampler

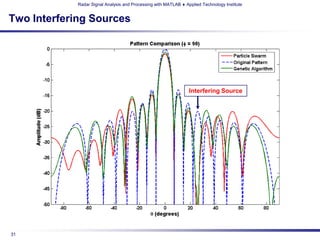
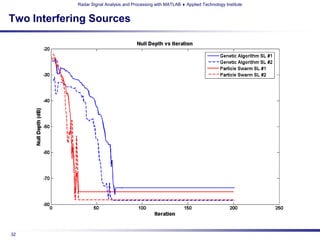
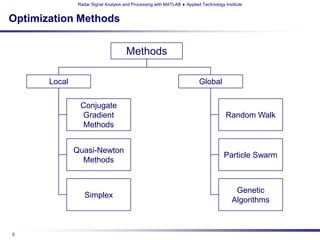
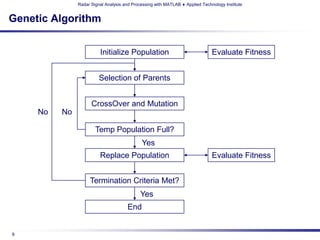
Professional Development Short Course On:
Radar Signal Analysis and Processing using MATLAB

Instructor:

Dr. Andy Harrison

ATI Course Schedule: http://www.ATIcourses.com/schedule.htm

http://www.aticourses.com/radar_signal_processing.htm
ATI's Radar Signal Analysis:

www.ATIcourses.com

Boost Your Skills 349 Berkshire Drive
Riva, Maryland 21140
with On-Site Courses Telephone 1-888-501-2100 / (410) 965-8805

Tailored to Your Needs
Fax (410) 956-5785
Email: ATI@ATIcourses.com

The Applied Technology Institute specializes in training programs for technical professionals. Our courses keep you
current in the state-of-the-art technology that is essential to keep your company on the cutting edge in today’s highly
competitive marketplace. Since 1984, ATI has earned the trust of training departments nationwide, and has presented
on-site training at the major Navy, Air Force and NASA centers, and for a large number of contractors. Our training
increases effectiveness and productivity. Learn from the proven best.

For a Free On-Site Quote Visit Us At: http://www.ATIcourses.com/free_onsite_quote.asp

For Our Current Public Course Schedule Go To: http://www.ATIcourses.com/schedule.htm

Radar Signal Analysis and Processing with MATLAB ♦ Applied Technology Institute

Global Optimization

 While LMS methods are computationally fast, quantization of the phase will
result in errors.

 Also, it is necessary to have receiver hardware at each element of the
phased array as well as an elaborate calibration technique.

 Global search methods can place very deep nulls in the desired directions,
while maintaining the characteristics of the antenna main beam.

 Since the solution space is predefined by the quantized amplitude and
phase coefficients of the particular antenna system, these global methods
do not require continuous amplitude and phase shifts.

 Additionally, these methods deal with the coherent output power of the
antenna array and therefore do not require receiver hardware at each
element in the antenna array.

2


Optimization Methods

Methods

Local Global

Conjugate
Gradient Random Walk
Methods

Quasi-Newton
Particle Swarm
Methods

Genetic
Simplex
Algorithms

3


Optimization Methods

Conjugate Random Genetic
Gradient Walk Algorithm
Global Optimization Poor Fair Good

Discontinuous Functions Poor Good Good

Non-differentiable Poor Good Good
Functions
Convergence Rate Good Poor Fair

4


Genetic Algorithms

 Genetic Algorithms (GA) are robust, stochastic-based search
methods, modeled on the concepts of natural selection.

 The strong survive to pass on their genes, while the weak are
eliminated from the population.

 Examples

 Design of layered material for broadband microwave absorbers.

 Extraction of natural resonance modes of radar targets from
backscattered response data.

 Economics, Ecology, Social Systems, Machine Learning, Chemistry,
Physics, etc.

5


Terminology

 Population – set of trial solutions.

 Generation – successively created populations.

 Parent – member of the current generation.

 Child – member of the next generation.

 Chromosome – coded form of a trial solution.

 Fitness – a chromosomes measure of goodness.

6


Chromosome Coding

 GAs operate on a coding of the parameters, instead of the
parameters themselves.

 In binary coding, the parameters are each represented by a finite-
length binary string.

 Chromosomes are the combination of all the encoded parameters.
(A string of ones and zeros)

 Binary coding yields very simple binary operators.

R1 L1 C1 R2 L2 C2
0101 1001 1101 1010 0001 0011

7


Genetic Algorithm

Initialize Population Evaluate Fitness

Selection of Parents

CrossOver and Mutation
No No

Temp Population Full?
Yes
Replace Population Evaluate Fitness

Termination Criteria Met?
Yes
End

8


Initialize Population

 Random Fill – The initial population is created by filling chromosomes
with random numbers.

 A Priori – Chromosomes in the initial population are created with
information about the solution.

9


Parent Selection

 Proportionate selection – Probability of selecting an individual is a
function of the individual’s relative fitness.

1
2
3
4
5
6
7
8
9

10


Parent Selection

 Tournament selection – N individuals are selected at random, the
individual with the highest fitness in the sub population is selected.

N Parent =
Population randomly selected Chromosome
chromosomes with best Fitness

11


Crossover and Mutation

 The crossover and mutation operations accept the parent
chromosomes and generate the children.

 Many variations of crossover have been developed, with single-point
crossover being the simplest.

 In mutation, an element in the chromosome is randomly selected
and changed.

12


Crossover and Mutation

 Single Point Crossover

Parent 1 a1 a2 a3 a4 a5 b1 b2 b3 b4 b5 Parent 2

Child 1 a1 a2 b3 b4 b5 b1 b2 a3 a4 a5 Child 2

 Mutation

a1 a2 a3 a4 a5 a6 a7

a1 a2 A3 a4 a5 a6 a7

13


Population Replacement

 Generational – The GA produces an entirely new generation of children,
which then replaces the parent generation.

 Steady-State – Only a portion of the current generation is replaced by
children.

14


Fitness Function

 The only connection between the physical problem and the GA.

 The value returned by the fitness function is proportional to the
goodness of a trial solution.

15


GA Optimization Guidelines

 Population Size: Typically 30 – 100
 Large populations enable faster convergence by providing more genetic
diversity. Smaller populations yield faster execution, especially for
complicated fitness functions.

 Probability of Crossover: Typically 0.6 – 0.9
 Crossover is the primary way a GA searches for new, better solutions.
A probability of 0.7 has been found to be optimal for a wide variety of
problems.

 Probability of Mutation: Typically 0.01 – 0.1
 The probability of mutation should generally be low. Mutation
introduces new genetic material into the search, but tends to push the
population’s average fitness away from the optimal value.

 Replacement Strategy: Generational vs. Steady-State
 Steady-state generally converges faster. Lower values of replacement
percentage usually converge faster.

16


Particle Swarm

 Originated in studies of bird flocking and fish schooling.

 The potential solutions (Particles) “fly” through the solution space
subject to both deterministic and stochastic rules.

 Particles are pulled toward the local and global best solution with
linear attraction forces.

17


Harmonious Flight

The ability of animal groups—such as this flock of starlings—to shift shape as one, even when they
have no leader, reflects the genius of collective behavior—something scientists are now tapping to
solve human problems.

National Geographic 2007
18


Particle Swarm

Initialize Swarm Evaluate Fitness

Update Velocities (Vn)
No
Update Positions (Xn) Evaluate Fitness

Termination Criteria Met?
Yes
End

19


Initialize Swarm

 Random Fill – The initial swarm is created by giving each particle a
random position and random velocity.

 A Priori – Particles in the initial swarm are created with information about
the solution.

20


Update Velocities

 Update the velocity of each particle toward the local and global best
position.

vn = ω ⋅ vn + κ1 ⋅ rand ⋅ (xlocal best ,n − xn )
   

+ κ 2 ⋅ rand ⋅ (x global best ,n − xn )
 

 Limit the velocity if necessary.

  v
if vn > vmax , then vn = n vmax
vn

21


Update Positions

 Update position using unit acceleration.

  
xn = xn + vn
 Clip position if necessary.

if xn ,d > xmax,d , then xn ,d = xmax,d
if xn ,d < xmin,d , then xn ,d = xmin,d

22


Particle Swarm Guidelines

 ω (Inertia) – Typical values between 0 – 1. This may be allowed to vary
randomly for each iteration or decrease with each iteration to encourage
local searching at the end of the process.

 κ1 , κ 2 (Memory & Cooperation) – Can be tuned for the particular
problem. Common practice in literature to set both equal in the range 1 –
2.

23


MATLAB Example

 Find the minimum of the following function.

24


MATLAB Example

 Find the minimum of the follow function.

25


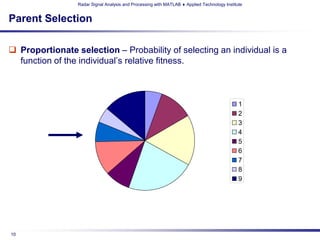
Antenna Pattern

 Suppose we want to minimize the antenna gain in a particular
direction due to an interfering source (Adaptive Nulling).

N M
AF (θ , φ ) = ∑∑ I mn e jβ mn e jα mn
n =1 m =1

I mn = Amplitude coefficient for each element

β mn = Phase shift for each element

2π
α mn = [xmn sin θ cos φ + ymn sin θ sin φ ]
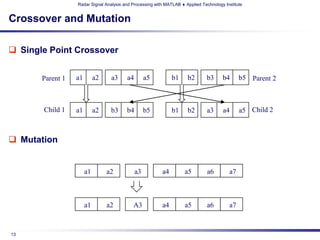
λ

26


Two Interfering Sources

 16 x 16 element planar array

 6 bit phase shifters, 3 bits used for nulling

 2 interfering sources located at
(θ = 18o, φ = 0o) and (θ = 26o, φ = 90o)

 50 Chromosomes / Particles

 200 Iterations

27



Location of
Interfering
Sources

28



Genetic Algorithm Particle Swarm

Nulls Placed in the Antenna Pattern
in the Direction of the Interfering Sources

29



Interfering Source

30



Interfering Source

31



32



 Main Beam Loss
 1.02 dB (Genetic Algorithm)
 1.63 dB (Particle Swarm)

 Beamwidth

Original GA PS
Φ = 0o

3 dB 6.29o 6.30o 6.35o

10 dB 10.48o 10.50o 10.60o

Φ = 90o

3 dB 6.29o 6.30o 6.35o
10 dB 10.48o 10.52o 10.59o

33

To learn more please attend ATI course
Radar Signal Analysis and Processing using MATLAB

Please post your comments and questions to our blog:
http://www.aticourses.com/blog/

Sign-up for ATI's monthly Course Schedule Updates :
http://www.aticourses.com/email_signup_page.html

ATI's Radar Signal Analysis and Processing using MATLAB Technical Training Short Course Sampler

More Related Content

What's hot

Viewers also liked

Similar to ATI's Radar Signal Analysis and Processing using MATLAB Technical Training Short Course Sampler

More from Jim Jenkins

Recently uploaded

ATI's Radar Signal Analysis and Processing using MATLAB Technical Training Short Course Sampler