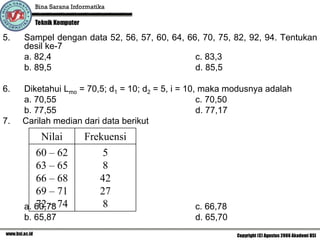
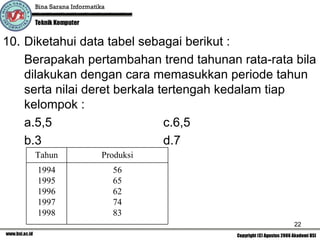
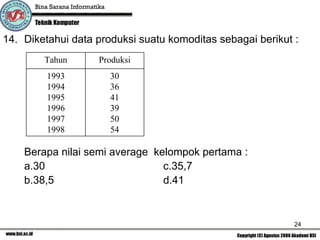
Dokumen ini adalah soal quiz untuk mata kuliah statistika deskriptif yang mencakup berbagai topik seperti pengolahan data, perhitungan statistika deskriptif, serta analisis deret waktu. Terdapat berbagai pertanyaan pilihan ganda yang mengharuskan mahasiswa untuk menggunakan kalkulator dalam menyelesaikannya. Isinya juga mencakup cara menghitung nilai rata-rata, median, modus, dan variasi, serta pengenalan metode peramalan dan indeks harga.