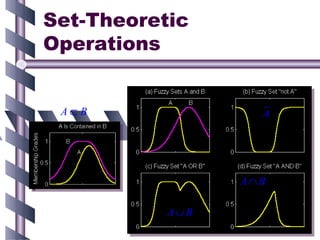
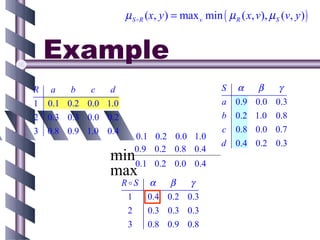
S: fuzzy relation defined on Y and Z. To find the composite relation R o S on X and Z: μR o S(x,z) = maxy [min(μR(x,y), μS(y,z))] For each x and z, find the maximum membership grade obtained by considering all possible y values and taking the minimum of the membership grades of R and S. This gives the generalized intersection-union definition of composition of fuzzy relations. It reduces to the usual composition rule when relations are crisp.

1. Fuzzy Logic
By Manoj Harsule

2. Overview
• A Little History
• Fuzzy Logic – A Definition
• Fuzzy set theory
• Introduction to fuzzy set
• Fuzzy Relations

3. A little History
 In the 1960’s Lotfi A. Zadeh Ph.D,. University of
California, Berkeley, published an obscure paper on
fuzzy sets . His unconventional theory allowed for
approximate information and uncertainty when
generating complex solutions; a process that
previously did not exist.
 Fuzzy Logic has been around since the mid 60’s but
was not readily excepted until the 80’s and 90’s.
Although now prevalent throughout much of the
world, China, Japan and Korea were the early
adopters

4. WHAT IS FUZZY LOGIC?
 Definition of fuzzy
 Fuzzy – “not clear, distinct, or not precise;
uncertain”
 Definition of fuzzy logic
A form of knowledge representation suitable for
notions that cannot be defined precisely, but which
depend upon their contexts.

5. TRADITIONAL REPRESENTATION OF
LOGIC
Slow (Low) Fast (High)
Speed = 0 Speed = 1

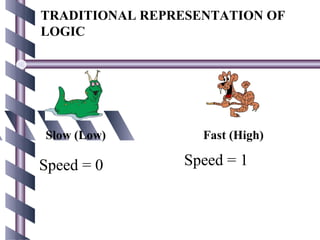
6. FUZZY LOGIC
REPRESENTATION
Slowest
For every [ 0.0 – 0.25 ]
problem Slow
must [ 0.25 – 0.50 ]
represent in Fast
terms of [ 0.50 – 0.75 ]
fuzzy sets. Fastest
[ 0.75 – 1.00 ]

7. Introduction to
Fuzzy Set Theory
Fuzzy Sets

8. Types of Uncertainty
• Stochastic uncertainty
– E.g., rolling a dice
• Linguistic uncertainty
– E.g., low price, tall people, young age
• Informational uncertainty
– E.g., credit worthiness, honesty

9. Crisp or Fuzzy Logic
• Crisp Logic
– A proposition can be true or false only.
• Ajay is a student (true)
• Smoking is healthy (false)
– The degree of truth is 0 or 1.
• Fuzzy Logic
– The degree of truth is between 0 and 1.
• Raj is young (0.3 truth)
• Amol is smart (0.9 truth)

10. Crisp Sets
• Classical sets are called crisp sets
– either an element belongs to a set or
not, i.e.,
x∈ A or
x∉ A
• Member Function of crisp set
0 x∉ A
µ A ( x) =  µ A ( x) ∈ { 0,1}
1 x ∈ A

11. Crisp Sets
P : the set of all people.
Y : the set of all young people. P
Y
Y
Young = { y y = age( x) ≤ 25, x ∈ P}
µYoung ( y )
1
25 y

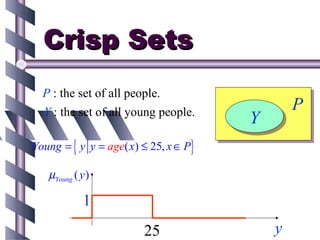
12. Crisp sets µ A ( x) ∈ { 0,1}
Fuzzy Sets
µ A ( x) ∈ [0,1]
Example
µYoung ( y )
1
y

13. Definition:
Fuzzy Sets and Membership
Functions
U : universe of discourse.
If U is a collection of objects denoted generically by x, then
a fuzzy set A in U is defined as a set of ordered pairs:
A = { ( x, µ A ( x)) x ∈ U }
membership
function
µ A : U → [0,1]

14. Example (Discrete
Universe)
U = {1, 2,3, 4,5, 6, 7,8}
# courses a student may take in a semester.
 (1, 0.1) (2, 0.3) (3, 0.8) (4,1) 
A=  #appropriate
 (5, 0.9) (6, 0.5) (7, 0.2) (8, 0.1)  courses taken
1
µA ( x )
0.5
0
2 4 6 8
x : # courses

15. Example (Discrete
Universe)
U = {1, 2,3, 4,5, 6, 7,8} # courses a student may
take in a semester.
 (1,0.1) (2,0.3) (3,0.8) (4,1)  appropriate
A=  
 (5,0.9) (6,0.5) (7,0.2) (8,0.1)  # courses taken
Alternative Representation:
A = 0.1/ 1 + 0.3 / 2 + 0.8 / 3 + 1.0 / 4 + 0.9 / 5 + 0.5 / 6 + 0.2 / 7 + 0.1/ 8

16. Example (Continuous
Universe)
U : the set of positive real numbers possible ages
B = { ( x, µ B ( x)) x ∈U }
1 about 50 years old
µ B ( x) = 4
 x − 50  1.2
1+  ÷ 1
 5  0.8
µ B ( x) 0.6
Alternative 0.4
Representation: 0.2
0
B=∫ 1
x 0 20 40 60 80 100
( )
4
x : age
R + 1+ x −50
5

17. Alternative Notation
A = { ( x, µ A ( x)) x ∈ U }
U : discrete universe A= ∑µ
xi ∈U
A ( xi ) / xi
U : continuous universe A = ∫ µ A ( x) / x
U
Note that ∑ and integral signs stand for the union of membership grades; “
/ ” stands for a marker and does not imply division.

18. Membership Functions
(MF’s)
• A fuzzy set is completely characterized by
a membership function.
– a subjective measure.
– not a probability measure.
“tall” in Asia
Membership
1
value
“tall” in USA
“tall” in Aus
0 height

19. Fuzzy Partition
• Fuzzy partitions formed by the linguistic
values “young”, “middle aged”, and “old”:

20. Introduction to
Fuzzy Set Theory
Set-Theoretic
Operations

21. Set-Theoretic
Operations
• Subset
A ⊆B ⇔µA ( x ) ≤ µ ( x ), ∀ ∈
B x U
• Complement
A = U − A ⇔ µA ( x ) = 1 − µA ( x )
• Union
C = A ∪ B ⇔ µC ( x ) = max( µA ( x ), µB ( x )) = µA ( x ) ∨ µB ( x )
Intersection
• C = A ∩ B ⇔ µ ( x) = min( µ
C A ( x ), µB ( x )) = µA ( x) ∧ µB ( x)

22. Set-Theoretic
Operations
A⊂ B A
A∩ B
A∪ B

23. Properties
Involution A=A
De Morgan’s laws
A∪ B = B ∪ A A∪ B = A∩ B
Commutativity A∩ B = B ∩ A
A∩ B = A∪ B
( A ∪ B) ∪ C = A ∪ ( B ∪ C )
Associativity ( A ∩ B ) ∩ C = A ∩ ( B ∩ C )
A ∩ ( B ∪ C ) = ( A ∩ B) ∪ ( A ∩ C )
Distributivity A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C )
A∪ A = A
Idempotence A∩ A = A
A ∪ ( A ∩ B) = A
Absorption A ∩ ( A ∪ B) = A

24. Properties
• The following properties are invalid
for fuzzy sets:
– The laws of contradiction
A∩ A = ∅
– The laws of excluded middle
A∪ A =U

25. Other Definitions for Set
Operations
• Union
µ A∪ B ( x) = min ( 1, µ A ( x) + µ B ( x) )
• Intersection
µ A∩ B ( x) = µ A ( x) ×µ B ( x)

26. Other Definitions for Set
Operations
• Union
µ A∪ B ( x ) = µ A ( x ) + µ B ( x ) − µ A ( x ) µ B ( x )
• Intersection
µ A∩ B ( x) = µ A ( x) ×µ B ( x)

27. Generalized
Union/Intersection
• Generalized Intersection
t-norm
• Generalized Union
t-conorm

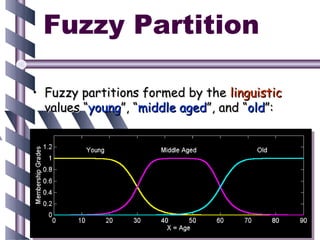
28. T-Norm
Or called triangular norm.
T :[0,1] × [0,1] → [0,1]
1. Symmetry T ( x, y ) = T ( y , x )
2. Associativity T (T ( x, y ), z ) = T ( x, T ( y, z ))
3. Monotonicity x1 ≤ x2 , y1 ≤ y2 ⇒ T ( x1 , y1 ) ≤ T ( x2 , y2 )
4. Border Condition T ( x,1) = x

29. T-Conorm Or called s-norm.
S :[0,1] × [0,1] → [0,1]
1. Symmetry S ( x, y ) = S ( y , x )
2. Associativity S ( S ( x, y ), z ) = S ( x, S ( y, z ))
3. Monotonicity x1 ≤ x2 , y1 ≤ y2 ⇒ S ( x1 , y1 ) ≤ S ( x2 , y2 )
4. Border Condition S ( x, 0) = x

30. Fuzzy Relations
Review
Fuzzy Relations

31. R ⊆ A×B
Binary Relation (R)
b1
a1
b2
A a2
a3
b3 B
b4
a4 b5
1 0 1 0 0 a1 Rb1 a1 Rb3 a2 Rb5
0 1
0 0 0 ( a1 , b1 ), ( a1 , b3 ), ( a2 , b5 ) 
MR =  R = 
1 0 0 1 0 ( a3 , b1 ), ( a3 , b4 ), ( a4 , b2 ) 
 
0 1 0 0 0 a3 Rb1 a3 Rb4 a4 Rb2

32. The Real-Life Relation
• x is close to y
– x and y are numbers
• x depends on y
– x and y are events
• x and y look alike
– x and y are persons or objects
• If x is large, then y is small
– x is an observed reading and y is a corresponding
action

33. Fuzzy Relations
A fuzzy relation R is a 2D MF:
R = { ( ( x, y ), µ R ( x, y ) ) | ( x, y ) ∈ X × Y }

34. R = { ( ( x, y ), µ R ( x, y ) ) | ( x, y ) ∈ X × Y }
Example (Approximate Equal)
X = Y = U = {1, 2,3, 4,5}
 1 0.8 0.3 0 0 
1 u−v = 0 0.8 1 0.8 0.3 0 
  
0.8 u − v = 1 M R =  0.3 0.8 1 0.8 0.3
µ R (u, v) = 
0.3 u − v = 2  
0 otherwise  0 0.3 0.8 1 0.8
 0
 0 0.3 0.8 1 


35. Max-Min Composition
X Y Z
R: fuzzy relation defined on X and Y.
S: fuzzy relation defined on Y and Z.
R 。 S: the composition of R and S.
A fuzzy relation defined on X an Z.
µ RoS (x, z ) = max y min ( µ R ( x, y ), µS ( y, z ) )
= ∨ y ( µ R ( x, y ) ∧ µ S ( y , z ) )

36. µ S o R (x, y ) = max v min ( µ R ( x, v), µ S (v, y ) )
Example
R a b c d S α β γ
1 0.1 0.2 0.0 1.0 a 0.9 0.0 0.3
2 0.3 0.3 0.0 0.2 b 0.2 1.0 0.8
3 0.8 0.9 1.0 0.4 c 0.8 0.0 0.7
0.1 0.2 0.0 1.0
d 0.4 0.2 0.3
0.9 0.2 0.8 0.4
min0.1 0.2 0.0 0.4
max
RoS α β γ
1 0.4 0.2 0.3
2 0.3 0.3 0.3
3 0.8 0.9 0.8

37. Max-min composition is not mathematically
tractable, therefore other compositions such as
max-product composition have been suggested.
Max-Product Composition
X Y Z
R: fuzzy relation defined on X and Y.
S: fuzzy relation defined on Y and Z.
R 。 S: the composition of R and S.
A fuzzy relation defined on X an Z.
µ RoS (x, z ) = max y ( µ R ( x, y ) µ S ( y, z ) )

38. Dimension Reduction
Projection
R
RY =  R ↓ Y 
  RX =  R ↓ X 
 

39. Dimension Reduction
Projection
R
RY =  R ↓ Y 
  RX =  R ↓ X 
 
= ∫ max µ R ( x, y ) / y = ∫ maxµ R ( x, y ) / x
Y x X y
µ RY ( y ) = max µ R ( x, y ) µ RX ( x) = max µ R ( x, y)
y
x

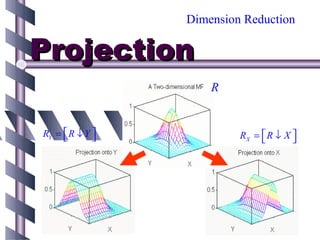
40. Dimension Expansion
Cylindrical Extension
A : a fuzzy set in X.
C(A) = [A↑X×Y] : cylindrical extension of A.
C ( A) = ∫ µ A ( x ) | ( x, y ) µC ( A ) ( x , y ) = µ A ( x )
X ×Y

41. Types of Fuzzy Relations
R ( x, x) = 1 for all x ∈ X
• Reflexive
– Irreflexive R ( x, x) ≠ 1 for some x ∈ X
– Antireflexive R ( x, x) ≠ 1 for all x ∈ X
– Epsilon Reflexive R ( x, x) ≥ ε for all x ∈ X
• Symmetric R ( x, y ) = R ( y, x) for all x ∈ X
– Asymmetric R ( x, y ) ≠ R( y, x) for some x ∈ X
– Antisymmetric R( x, y ) > 0 and R( y, x) > 0 → x = y for all x, y ∈ X

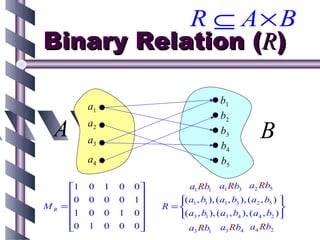
42. Types of Fuzzy Relations
• Transitive (max-min transitive)
R ( x, z ) ≥ max min[ R ( x, y ), R ( y , z )] for all x,z ∈X
y∈Y
– Non-transitive:
For some (x,z), the above do not satisfy.
– Antitransitive:
R ( x, z ) < max min[ R ( x, y ), R ( y , z )] for all x,z ∈X
y∈Y
• Example: X = Set of cities, R=“very far”
Reflexive, symmetric, non-transitive

43. Types of Fuzzy Relations
• Transitive Closure
– Crisp: Transitive relation that contains
R(X,X) with fewest possible members
– Fuzzy: Transitive relation that contains
R(X,X) with smallest possible
membership
– Algorithm:
1. R ' = R ∪ R o R ).
(
2. If R ' ≠ R, make R = R ' and go to step 1
3. Stop : R ' = RT

44. Types of Fuzzy Relations
• Fuzzy Equivalence or Similarity
Relation
– Reflexive, symmetric, and transitive
– Decomposition:
R=  ααR
⋅
α∈ ,1]
[0
α
R is a crisp equivalence relation.
Set of partitions :
∏ ={π(αR ) | α∈
(R) [0,1]}
– Partition Tree

45. Types of Fuzzy Relations
• Fuzzy Compatibility or Tolerance Relation
– Reflexive and symmetric
– Maximal compatibility class and complete cover
• Compatibility class Subset A of X such that < x, y >∈R
• Maximal compatibility class: largest compatibility
class
• Complete cover: Set of maximal compatibility
classes
– Maximal alpha-compatibility class
– Complete alpha-covers
– Note:
Relation from distance metrics forms tolerance
relation in clustering.

46. Bibliography
• J. R. Jang, C. Sun, E. Mizutani,
“Neuro-Fuzzy and Soft Computing: A
Computational Approach to Learning
and Machine Intelligence, Prentice
Hall
• Slides and notes:
http://equipe.nce.ufrj.br/adriano/fuzzy/bib