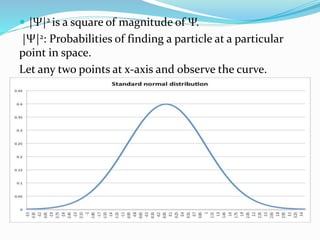
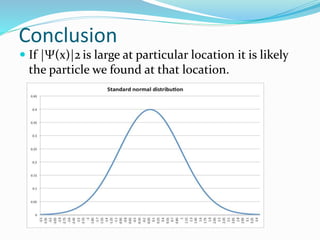
The document discusses key concepts in quantum mechanics including wave functions, probability, operators, expectation values, and normalization. Some main points: - The wave function Ψ is a complex function that represents the quantum state of a system and |Ψ|2 gives the probability of finding a particle in a particular location. - Operators connect the wave function to observable physical quantities. Expectation values provide the average value that would be obtained from many measurements. 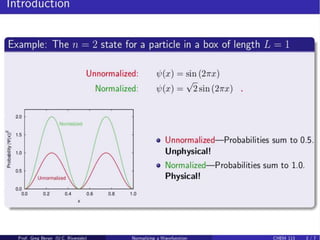- For a wave function to represent a physical state, it must be normalized such that the total probability across all possible values equals 1.

2. Wave Function
 It is denoted by Ψ, It is function of (x,y,z,t). It is
complex function, it represents the state of system.
Complex function Ψ =2+3i
It does not tell us with certainty what the observable
systems are? It gives us only probabilities, complex
functions never be observable.
Quantum mechanics based on Heisenberg uncertainty
principle, It does not describe system perfectly. It gives
only probabilities |Ψ|2

3.  |Ψ|2 is a square of magnitude of Ψ.
|Ψ|2: Probabilities of finding a particle at a particular
point in space.
Let any two points at x-axis and observe the curve.

4. Physical Significance
 Wave mechanics is connected to a quantity called wave
function and is denoted through Ψ.
 The probability of that particle will found at a given
place in the space at a given instant.
 As Ψ gives us probability , if |Ψ|2 have large value it
means at a particular location it is likely that a particle
will found at that location
Particle between x1 to x2 =
x1
x2
|Ψ(x)|2

5. Probability
• A function of continuous random variables whose integral
across an interval gives the probability that value of variable
lies within the same interval.
• Probability is key feature to quantum mechanics its
fundamental source is Ψ.
• Ψ is complex function which is not observable. So, we
consider probability density which is observable.
P(x)=|Ψ(x) |2
P(x)= 𝑎
𝑏
Ψ∗(x)Ψ(x)𝑑𝑥

6. Conclusion
 If |Ψ(x)|2 is large at particular location it is likely
the particle we found at that location.

7. Operators
 “An operator is a mathematical instruction or procedure
to be carried out on a function so as to get another
function”.
 When they operate on a function they give us physical
quantity. In other words we can say that they connect
wave function Ψ(x) with a observable quantity.
𝑄 , 𝑥, 𝑝 etc.

8. Mathematical relations of
Operators
 Suppose 𝐴 & 𝐵 are two different operators and X be an
operand then
( 𝐴 + 𝐵)𝑋 = 𝐴𝑋 + 𝐵𝑋
( 𝐴 − 𝐵)𝑋 = 𝐴𝑋 − 𝐵𝑋
First 𝐵 will operate to get X′
& then 𝐴 to give X′′o
𝐴 𝐵𝑋 = 𝑋′′

9. Operators
Unityoperator: It leaves any ket unchanged,
𝐼 Ψ = Ψ

10. Expectation value
 It is defined as “average value from repeated
measurements of an identically prepared quantum
state”.
It is denoted by <x>.
The expectation value ⟨ 𝐴⟩ of 𝐴 with
respect to a state Ψ is defined by
For example;

11. We can interpret
⟨ 𝐴⟩ as an average of a series of measurements of A.
That is the expectation value of an observable , which is obtained by adding all
permissible eigenvalues an, with each an multiplies by the corresponding
probability Pn. It is valid only for discrete spectra.
Above relation can be extended for continuous spectra as follows.

12.  prepare a very large number of identical systems each
in the same state Ψ .
 The observable A is then measured on all these
identical systems; the results of these measurements
are a1,a2,….,an
 the corresponding probabilities of occurrence are
P1,P2,………,Pn.
 The average value of all these repeated measurements
is called the expectation value of A with respect to the
state Ψ .

13. Calculate expectation value for position for
following wave function between 0 to 2π
 <x>= 0
2𝜋
Ψ∗(x)Ψ(x)𝑑𝑥
= 0
2𝜋
(
1
2𝜋
𝑒 − inx)Ψ(
1
2𝜋
𝑒 − inx)𝑑𝑥
= 1
2𝜋 𝑎
𝑏
(𝑥𝑒
_inx+inx)𝑑𝑥
=
1
2𝜋
2𝜋
2
2 − 0 2
=
1
2𝜋
×
4𝜋2
2
<x> = 𝜋

14. Calculate expectation value for momentum for following
wave function between 0 to 2π
< 𝑝>= 0
2𝜋
Ψ∗(x)pΨ(x)𝑑𝑥
= 0
2𝜋
(
1
2𝜋
𝑒 − inx)Ψ 𝑝(
1
2𝜋
𝑒 − inx)𝑑𝑥
=
1
2𝜋 0
2𝜋
(𝑥𝑒
_inx)−𝑖 ћ
𝜕
𝜕𝑥
(𝑒 − inx)𝑑𝑥
=
1
2𝜋 0
2𝜋
(𝑥𝑒
_inx)−𝑖 ћ
𝜕
𝜕𝑥
(𝑒 − inx)𝑑𝑥

15. =
1
2𝜋 0
2𝜋
(𝑥𝑒
_inx)−𝑖 ћ
𝜕
𝜕𝑥
(𝑒inx)𝑑𝑥
=
1
2𝜋 0
2𝜋
(𝑥𝑒
_inx+inx)(−𝑖 ћ)(𝑖𝑛)𝑑𝑥
=
1
2𝜋 0
2𝜋
(−𝑖 ћ)(𝑖𝑛)𝑑𝑥
=
1
2𝜋 0
2𝜋
(−𝑖2ћ𝑛)𝑑𝑥
=
1
2𝜋 0
2𝜋
(ћ𝑛)𝑑𝑥
=
1
2𝜋
(2𝜋ћ𝑛 − 0)
=
1
2𝜋
(2𝜋ћ𝑛 − 0)
< 𝑝>=ћn

16. Normalization
 The P has to be normalized, that total sum of all
probable outcomes is equal to 1.
−∝
+∝
𝐹 𝑥 𝑑𝑥 = 1
In terms of wave function
−∝
+∝
|Ψ|2 𝑑𝑥 = 1
Infinite wave function is not normalized.

17.  Normalizing a wave function just means multiplying
it by a constant to ensure that the sum of the
probabilities for finding the particle equals 1.