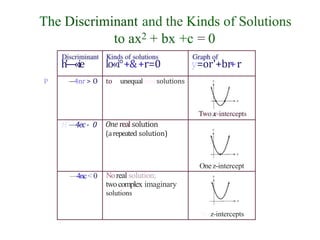
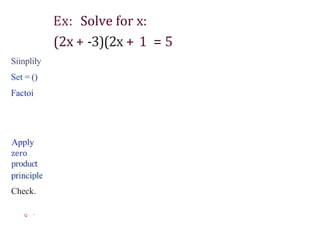The document explains quadratic equations, detailing their standard form and methods for solving them, including factoring, the zero-product principle, completing the square, and the quadratic formula. It also describes the Pythagorean theorem and provides examples demonstrating each method's application. Key steps and common errors in solving these equations are highlighted for better understanding.

1. Ouadratic Equations
Start p 145 graph and model for #131 & discuss.

2. Definition of a Quadratic Equation
Aquadratic equation in x is an equation that
can be written in the standard form
ax2 + bx + c = 0
where n, b, and c are real numbers with n no/
equal to 0. A quadratic equation in x is also
called a second-degree polynomial
equation in x.

3. The Zero-Product Principle
If the product of two algebraic expressions is
zero, then at least one of the factors is equal
to zero.
If AB —
—
0, then A —
—
0 or B —
—
0.

4. Solving a Quadratic Equation by
Factoring
1. If necessary, rewrite the equation in the
form ex2 + bx + c = 0, moving all terms
to one side, thereby obtaining on
the other side.
2. Factor.
3. Set each factor = zero. (Apply the zero—
product principle.)
4. Solve the equations in step 3.
5. Check the solutions in the
equation.

5. Text Example
• Solve 2x2 + 7x —
4 by factoring and then
using the zero—product principle. (Donotlook
at notes, no need to write.)
Step 1 Move all terms to one side and
obtain zero on the other side. Subtract 4
from both sides and write the equation in
standard form.
2r2 + 7x —4 = 4 —
4
2r2 + 7x —4 = 0
Step 2 Factor.

6. Solution cont.
• Solve 2x2 + 7x = 4 by factoring and then using the zero—product
principle.
Steps 3 and 4 Set each factor equal to
zero and solve each resulting equation.
or x + 4 = 0
x = —
4
2 x —
1 = 0
2 x = 1
x = 1/2
Steps 5 check your solution (by putting
each solution back into the ORIGINAL
equation to see if it yields a TRUE
statement.

7. Siinpliły
Set = ()
Factoi
Apply
zero
product
Check.
Q '
Ex: Solve for x:
(2x + -3)(2x + 1 = 5

8. The Square Root Method
If u is an algebraic expression and d is a positive real
number, then u2 = d has exactly two solutions.
If u2 = d, then u = Jff
Equivalently,
If u2 = d then u = 1 ,f@
or u = - d
We only use this method if the variable is originally
contained within a “squared part”. Ex: x2-8=12 or
(2x-4)2-5=20. Can you think of a counter
example? Do:
5(4.—1)2
= —
12

9. Text Example
What term should be added to the binomial
x2 + 8x so that it becomes a perfect square
trinomial? Then write and factor the
trinomial.
8x -t
2+ 2
)2
Note: this is still an expression, not an equation.
Do (factor by completing the square- see instructions next
slide first) p 144 # 54.
x2
+6x —
5 = 0

10. Completing the Square
If x2 + bx is a binomial, then by adding (b/2) 2, which is
the square of half the coefficient of x, a perfect square
trinomial will result. That is,
x2 + bx + (b/2)2= (x + b/2)2
That is, take half of the coefficient of the x term, square
it, and add it to each side.
Then take +/ the square root of each side. (Square root
method.)
Note: this is really just using the fact that the square of a
binomial results in a perfect square trinomial. We are
just “completing” the perfect square trinomial.

11. Solving the Quadratic Formula
Given a quadratic equation in the form:
pq2
a>O,
a,b,c integers
We can solve for x by “plugging in” a, b and c:
b2
4oc
2d
Derived by completing the square, if interested, see p121.

12. Ex: Solve by using the quadratic formula:
Put into torn
Identify a,b,c
Plug in
Simplify
Common errors:
Not writing the division bar all the way.
b ITI tins —
(whalcvci b is!). In this casc —(-8) = 8.

13. h
'
—
«ie lo«i°+&+r=0 y=or'+br
+r
—
4nr > O to unequal realsolutions
H —4ec- 0 One realsolution
(arepeated solution)
Onez-intercept
—4nc< 0 Noreal solution;
twocomplex imaginary
solutions
Noz-intercepts
The Discriminant and the Kinds of Solutions
to ax2 + bx +c = 0
P

14. Which approach do we use to solve a quadratic equation?
1. Recognize that you have a quadratic equation.
2. If the variable is isolated within the “s uared art”,
isolate the squared part, take +/- square root of each
side, then isolate the variable. (Square root method.)
Otherwise set = 0
3.
a. If it is EASY to factor, factor, set each factor
equal to zero and solve for the variable (Factoring
method.)
b. If it is NOT eas to factor, plug a, b, and c
into the quadratic formula and simplify (Quadratic
formula method.)
4. If it says to solve by completing the square, do so
(Completing the square method.)

15. The Pythagorean Theorem
The sum of the squares of the lengths of the
legs of a right triangle equals the square of
the length of the hypotenuse.
If the legs have lengths a and b, and the
hypotenuse has length c, then
a2 -t b2 = C2 do 4 pl44:105, 138 (set up)
das o csv ion if‹a vr s "'