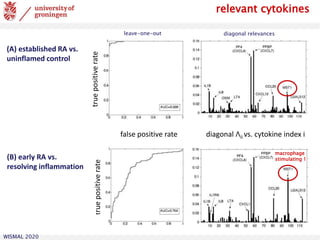
The document reviews prototype-based models in machine learning, focusing on both supervised and unsupervised learning techniques such as vector quantization and self-organizing maps. It discusses various methodologies, their applications, and challenges related to performance, including classification, regression, and dimensionality reduction. An application example highlights the use of these techniques for early diagnosis of rheumatoid arthritis based on cytokine expression analysis.

1. Michael Biehl
Bernoulli Institute for
Mathematics, Computer Science
and Artificial Intelligence
University of Groningen
www.cs.rug.nl/biehl
Prototype-based models
in machine learning

2. WISMAL 2020 2
review: WIRES Cognitive Science (2016)

3. WISMAL 2020 3
overview
1. Introduction / Motivation
prototypes, exemplars
neural activation / learning
3. Supervised Learning
Learning Vector Quantization (LVQ)
Adaptive distances and Relevance Learning
(Example: early diagnosis of rheumatoid arthritis)
2. Unsupervised Learning
Vector Quantization (VQ)
Competitive Learning in VQ and Neural Gas
Kohonen’s Self-Organizing Map (SOM)
(Example: tissue specific gene expression )
4. Summary

4. WISMAL 2020 4
1. Introduction
prototypes, exemplars:
representation of information in terms of
typical representatives (e.g. of a class of objects),
much debated concept in cognitive psychology
neural activation / learning:
external stimulus to a network of neurons
response acc. to weights (expected inputs)
best matching unit (and neighbors)
learning -> even stronger response to the same stimulus in future
weights represent different expected stimuli (prototypes)
here “only”: framework for machine learning based data analysis

5. WISMAL 2020 5
even independent from the above:
attractive framework for machine learning based data analysis
- trained system is parameterized in the feature space (data)
- facilitates discussions with domain experts
- transparent (white box) and provides insights into the
applied criteria (classification, regression, clustering etc.)
- easy to implement, efficient computation
- versatile, successfully applied in many different application areas

6. WISMAL 2020 6
2. Unsupervised Learning
Some potential aims:
dimension reduction:
- compression
- visualization for human insight
- principal {independent} component analysis
exploration / structure detection:
- clustering
- similarities / dissimilarities
- source identification
- density estimation
- neighborhood relation, topology
pre-processing for further analysis
- supervervised learning, e.g.
classification, regression, prediction

7. WISMAL 2020
based on dis-similarity/distance measure
assignment to prototypes:
given vector xμ , determine winner
→ assign xμ to prototype w*
one popular example: (squared) Euclidean distance
Vector Quantization (VQ)
VQ system: set of prototypes
data: set of feature vectors
Vector Quantization: identify (few) typical representatives of data
which capture essential features

8. WISMAL 2020 8
random sequential (repeated) presentation of data
… the winner takes it all:
initially: randomized wk, e.g. in randomly selected data points
competitive learning
η (<1): learning rate, step size of update
comparison:
K-means: updates all prototypes, considers all data at a time,
EM for Gaussian mixtures in the limit of zero width
competitive VQ: updates only the winner, random sequ. presentation
of single examples (stochastic gradient descent)

9. WISMAL 2020 9
quantization error
here:
Euclidean distance
competitive VQ (and K-means) aim at optimizing a cost function:
- assign each data to closest prototype
- measure the corresponding (squared) distance
quantization error (sum over all data points)
measures the quality of the representation
defines a (one) criterion to evaluate / compare
the quality of different prototype configurations
 
1 for x 0
Θ =
0 else
x




10. WISMAL 2020 10
VQ and clustering
ideal clustering
scenario:
well-separate,
spherical clusters
in general:
representation
of observations
in feature space
sensitive to
cluster shape,
coordinate
transformations
(even linear)
small clusters
irrelevant with
respect to quan-
tization error
Remark 1: VQ ≠ clustering
minimal quantization error:

11. WISMAL 2020 11
VQ and clustering
Remark 2: clustering is an ill-defined problem
“obviously three clusters” “well, maybe only two?”
our criterion: lower HVQ higher HVQ
→ “ better clustering ” ???

12. WISMAL 2020 12
→ “ the best clustering ” ?
HVQ = 0
K=1
the simplest clustering …
HVQ (and similar criteria) allow only to compare VQ with the same K !
K=60
more general: heuristic compromise between “error” and “simplicity”
VQ and clustering

13. WISMAL 2020 13
data
initial
prototypes
practical issues of VQ training:
solution: rank-based updates (winner, second, third,… )
dead
units
training
more general: local minima of the quantization error,
initialization-dependent outcome of training
competitive learning

14. WISMAL 2020
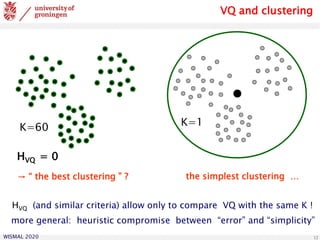
Neural Gas (NG)
introduce rank-based neighborhood cooperativeness:
upon presentation of xμ :
• determine the rank of the prototypes
• update all prototypes:
with neighborhood function
and rank-based range λ
• potential annealing of λ from large to smaller values
[Martinetz, Berkovich, Schulten, IEEE Trans. Neural Netw. 1993]
many prototypes (gas) to represent the density of observed data

15. WISMAL 2020
Self-Organizing Map
T. Kohonen. Self-Organizing Maps. Springer (2nd edition 1997)
neighborhood cooperativeness on a predefined low-dim. lattice
lattice A of neurons
i.e. prototypes
- update winner and neighborhood:
where
range ρ w.r.t. distances in lattice A
upon presentation of xμ :
- determine the winner (best matching unit)
at position s in the lattice

16. WISMAL 2020 16
- lattice deforms reflecting the density of observation
© Wikipedia
SOM provides topology preserving low-dim representation
e.g. for inspection and visualization of structured datasets
Self-Organizing Map
(2d lattice and 2d data)

17. WISMAL 2020 17
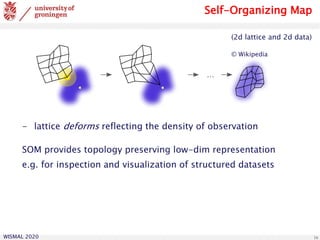
Self-Organizing Map
illustrative example: Iris flower data set [Fisher, 1936]:
4 num. features representing Iris flowers from 3 different species
SOM (4x6 prototypes in a 2-dim. grid)
training on 150 samples (without class label information)
component planes: 4 arrays representing the prototype values

18. WISMAL 2020 18
U-Matrix: elements
Ur = average distance
d(wr,ws) from n.n. sites
reflects cluster structure
larger U at cluster borders
post labelling: assign
prototype to the majority
class of data it wins
Versicolor
Setosa
Virginica
(undefined)
here: Setosa well separated
from Virginica/Versicolor
Self-Organizing Map

19. WISMAL 2020 19
Remarks:
- presentation of approaches not in historical order
- many extensions of the basic concept, e.g.
cost-function based SOM [Heskes, 1999]
Generative Topographic Map (GTM), statistical modelling
formulation of the mapping to low-dim. lattice
[Bishop, Svensen, Williams, 1998]
SOM and NG for specific types of data
- time series
- “non-vectorial” relational data
- graphs and trees
Vector Quantization/SOM

20. WISMAL 2020 20
3. Supervised Learning
Potential aims:
- classification:
assign observations (data) to categories or classes
as inferred from labeled training data
- regression:
assign a continuous target value to an observation
- prediction:
predict the evolution of a time series (sequence)
inferred from observations of the history
Learning from examples -> hypothesis -> application to novel data

21. WISMAL 2020 21
distance based classification
assignment of data (objects, observations,...)
to one or several classes (crisp/soft) (categories, labels)
based on comparison with reference data (samples, prototypes)
in terms of a distance measure (dis-similarity, metric)
representation of data (a key step!)
- collection of qualitative/quantitative descriptors
- vectors of numerical features
- sequences, graphs, functional data
- relational data, e.g. in terms of pairwise (dis-) similarities

22. WISMAL 2020
K-NN classifier
a simple distance-based classifier
- store a set of labeled examples
- classify a query according to the
label of the Nearest Neighbor
(or the majority of K NN)
- local decision boundary acc.
to (e.g.) Euclidean distances
?
- piece-wise linear class borders
parameterized by all examples
feature space
+ conceptually simple, no training required, one parameter (K)
- expensive storage and computation, sensitivity to “outliers”
can result in overly complex decision boundaries

23. WISMAL 2020
prototype based classification
a prototype based classifier [Kohonen 1990, 1997]
- represent the data by one or
several prototypes per class
- classify a query according to the
label of the nearest prototype
(or alternative schemes)
- local decision boundaries according
to (e.g.) Euclidean distances
- piece-wise linear class borders
parameterized by prototypes
feature space
?
+ less sensitive to outliers, lower storage needs, little computational
effort in the working phase
- training phase required in order to place prototypes,
model selection problem: number of prototypes per class, etc.

24. WISMAL 2020
set of prototypes
carrying class-labels
based on dissimilarity/distance measure
nearest prototype classifier (NPC):
given - determine the winner
- assign x to the class
most prominent example: (squared) Euclidean distance
Nearest Prototype Classifier
reasonable requirements:

25. WISMAL 2020
∙ identification of prototype vectors from labeled example data
∙ distance based classification (e.g. Euclidean)
Learning Vector Quantization
N-dimensional data, feature vectors
• initialize prototype vectors
for different classes
heuristic scheme: LVQ1 [Kohonen, 1990, 1997]
• identify the winner
(closest prototype)
• present a single example
• move the winner
- closer towards the data (same class)
- away from the data (different class)

26. WISMAL 2020
∙ identification of prototype vectors from labeled example data
∙ distance based classification (e.g. Euclidean)
Learning Vector Quantization
N-dimensional data, feature vectors
∙ tesselation of feature space
[piece-wise linear]
∙ distance-based classification
[here: Euclidean distances]
∙ generalization ability
correct classification of new data
∙ aim: discrimination of classes
( ≠ vector quantization
or density estimation )



27. WISMAL 2020
sequential presentation of labelled examples
… the winner takes it all:
learning rate
many heuristic variants/modifications: [Kohonen, 1990,1997]
- learning rate schedules ηw (t)
- update more than one prototype per step
iterative training procedure:
randomized initial , e.g. close to the class-conditional means
LVQ1
LVQ1 update step:

28. WISMAL 2020
LVQ1 update step:
LVQ1-like update for
generalized distance:
addtl. requirement:
update decreases (increases) distance if classes coincide (are different)
LVQ1

29. WISMAL 2020
Generalized LVQ
one example of cost function based training: GLVQ [Sato & Yamada, 1995]
sigmoidal (linear for small arguments), e.g.
E approximates number of misclassifications
linear
E favors large margin separation of classes, e.g.
two winning prototypes:
minimize

30. WISMAL 2020
GLVQ
training = optimization with respect to prototype position,
e.g. single example presentation, stochastic sequence of examples,
update of two prototypes per step
based on non-negative, differentiable distance

31. WISMAL 2020
GLVQ
training = optimization with respect to prototype position,
e.g. single example presentation, stochastic sequence of examples,
update of two prototypes per step
based on non-negative, differentiable distance

32. WISMAL 2020
GLVQ
training = optimization with respect to prototype position,
e.g. single example presentation, stochastic sequence of examples,
update of two prototypes per step
based on Euclidean distance
moves prototypes towards / away from
sample with prefactors

33. WISMAL 2020
+ frequently applied in a
variety of practical problems
+ intuitive interpretation
prototypes defined in feature space
+ natural for multi-class problems
- often based on purely heuristic arguments … or …
cost functions with unclear relation to classification error
Important issue: which is the ‘right’ distance measure ?
prototype/distance based classifiers
- model/parameter selection (# of prototypes, learning rate, …)
features may
- scale differently
- be of completely different nature
- be highly correlated / dependent
…
simple Euclidean distance ?
+ flexible, easy to implement

34. WISMAL 2020 34
distance measures
fixed distance measures:
- select distance measures according to prior knowledge
- data driven choice in a preprocessing step
- determine prototypes for a given distance
- compare performance of various measures
example: divergence based LVQ

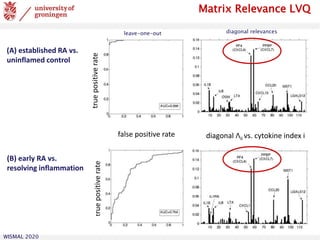
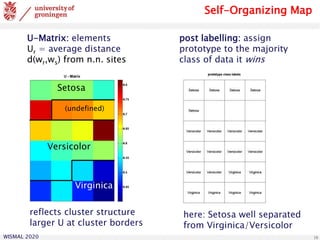
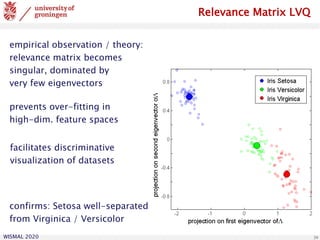
35. WISMAL 2020
Relevance Matrix LVQ
generalized quadratic distance in LVQ:
variants:
one global, several local, class-wise relevance matrices
→ piecewise quadratic decision boundaries
rectangular discriminative low-dim. representation
e.g. for visualization [Bunte et al., 2012]
possible constraints: rank-control, sparsity, …
normalization:
diagonal matrices: single feature weights [Bojer et al., 2001]
[Hammer et al., 2002]
[Schneider et al., 2009]

36. WISMAL 2020
Generalized Relevance Matrix LVQ
Generalized Matrix-LVQ
(GMLVQ)
gradients of GLVQ cost fct.:
optimization of prototypes and distance measure

37. WISMAL 2020 37
heuristic interpretation
summarizes
- the contribution of the original dimension
- the relevance of original features for the classification
interpretation assumes implicitly:
features have equal order of magnitude
e.g. after z-score-transformation →
(averages over data set)
standard Euclidean distance for
linearly transformed features

38. WISMAL 2020 38
Iris flower data revisited (supervised analysis by GMLVQ)
GMLVQ
prototypes
relevance
matrix
Relevance Matrix LVQ

39. WISMAL 2020 39
empirical observation / theory:
relevance matrix becomes
singular, dominated by
very few eigenvectors
prevents over-fitting in
high-dim. feature spaces
facilitates discriminative
visualization of datasets
confirms: Setosa well-separated
from Virginica / Versicolor
Relevance Matrix LVQ

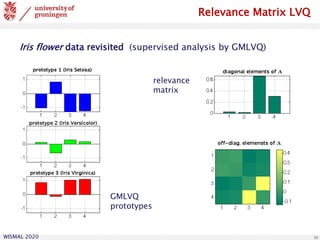
40. WISMAL 2020
projection on first eigenvector
projectiononsecondeigenvector a multi-class example
classification of coffee samples
based on hyperspectral data
(256-dim. feature vectors)
[U. Seiffert et al., IFF Magdeburg]
prototypes

41. WISMAL 2020
Relevance Matrix LVQ
optimization of
prototype positions
distance measure(s)
in one training process
(≠ pre-processing)
motivation:
improved performance
- weighting of features and pairs of features
simplified classification schemes
- elimination of non-informative, noisy features
- discriminative low-dimensional representation
insight into the data / classification problem
- identification of most discriminative features
- intrinsic low-dim. representation, visualization

42. WISMAL 2020
related schemes
Relevance LVQ variants
local, rectangular, structured, restricted... relevance matrices
for visualization, functional data, texture recognition, etc.
relevance learning in Robust Soft LVQ, Supervised NG, etc.
combination of distances for mixed data ...
Relevance Learning related schemes in supervised learning ...
RBF Networks [Backhaus et al., 2012]
Neighborhood Component Analysis [Goldberger et al., 2005]
Large Margin Nearest Neighbor [Weinberger et al., 2006, 2010]
and many more!
Linear Discriminant Analysis (LDA)
~ one prototype per class + global matrix,
different objective function!

43. WISMAL 2020
An application example:
Early diagnosis of Rheumatoid Arthritis
Expression of chemokines CXCL4 and CXCL7 by synovial
macrophages defines an early stage of rheumatoid arthritis
Annals of the Rheumatic Diseases 75:763-771 (2016)
L. Yeo, N. Adlard, M. Biehl, M. Juarez, M. Snow
C.D. Buckley, A. Filer, K. Raza, D. Scheel-Toellner

44. WISMAL 2020
uninflamed control established RA early inflammation
resolving early RA
cytokine based diagnosis of RA
at earliest possible stage ?
ultimate goals:
understand pathogenesis and
mechanism of progression
rheumatoid arthritis (RA)

45. WISMAL 2020 45
Rheumatoid Arthritis
Rheumatoid Arthritis (RA)
- chronicle inflammatory disease
- immune system affects joints
- RA leads to deformation and disability

46. WISMAL 2020
mRNA extraction real-time PCRtissue sectionsynovium
synovial tissue cytokine expression
IL1A IL17F FASL CXCL4 CCL15 TGFB1 KITLG
IL1B IL18 CD70 CXCL5 CCL16 TGFB2 MST1
IL1RN IL19 CD30L CXCL6 CCL17 TGFB3 SPP1
IL2 IL20 4-1BB-L CXCL7 CCL18 EGF SFRP1
IL3 IL21 TRAIL CXCL9 CCL19 FGF2 ANXA1
IL4 IL22 RANKL CXCL10 CCL20 TGFA TNFRSF13B
IL5 IL23A TWEAK CXCL11 CCL21 IGF2 IL6R
IL6 IL24 APRIL CXCL12 CCL22 VEGFA NAMPT
IL7 IL25 BAFF CXCL13 CCL23 VEGFB C1QTNF3
IL8 IL26 LIGHT CXCL14 CCL24 MIF VCAM1
IL9 IL27 TL1A CXCL16 CCL25 LIF LGALS1
IL10 IL28A GITRL CCL1 CCL26 OSM LGALS9
IL11 IL29 FASLG CCL2 CCL27 ADIPOQ LGALS3
IL12A IL32 IFNA1 CCL3 CCL28 LEP LGALS12
IL12B IL33 IFNA2 CCL4 XCL1 GHRL
IL13 LTA IFNB1 CCL5 XCL2 RETN
IL14 TNF IFNG CCL7 CX3CL1 CTLA4
IL15 LTB CXCL1 CCL8 CSF1 EPO
IL16 OX40L CXCL2 CCL11 CSF2 TPO
IL17A CD40L CXCL3 CCL13 CSF3 FLT3LG
panel of 117 cytokines
• cell signaling proteins
• regulate immune response
• produced by, e.g.
T-cells, macrophages,
lymphocytes, fibroblasts, etc.

47. WISMAL 2020
GMLVQ analysis
pre-processing:
• log-transformed expression values
• 21 leading principal components explain 95% of the variation
Two two-class problems: (A) established RA vs. uninflamed controls
(B) early RA vs. resolving inflammation
• 1 prototype per class, global relevance matrix, distance measure:
• leave-two-out validation (one from each class)
evaluation in terms of Receiver Operating Characteristics

48. WISMAL 2020
false positive rate
truepositiveratetruepositiverate
diagonal Λii vs. cytokine index i
(A) established RA vs.
uninflamed control
(B) early RA vs.
resolving inflammation
Matrix Relevance LVQ
diagonal relevancesleave-one-out

49. WISMAL 2020
CXCL4 chemokine (C-X-C motif) ligand 4
CXCL7 chemokine (C-X-C motif) ligand 7
direct study on protein level, staining / imaging of sinovial tissue:
macrophages : predominant source of CXCL4/7 expression
protein level studies
• high levels of CXCL4 and
CXLC7 in early RA
• expression on macrophages
outside of blood vessels
discriminates
early RA / resolving cases

50. WISMAL 2020
false positive rate
truepositiveratetruepositiverate
diagonal Λii vs. cytokine index i
(A) established RA vs.
uninflamed control
(B) early RA vs.
resolving inflammation
relevant cytokines
macrophage
stimulating 1
diagonal relevancesleave-one-out

51. WISMAL 2020 51
http://matlabserver.cs.rug.nl/gmlvqweb/web/
Matlab code:
Relevance and Matrix adaptation in Learning Vector
Quantization, including GRLVQ, GMLVQ and LiRaM LVQ (K. Bunte):
http://www.cs.rug.nl/~biehl/
links
links, pre- and re-prints etc.:
No-nonsense beginners’ tool for GMLVQ:
http://www.cs.rug.nl/~biehl/gmlvq
Sci-Kit compatible Python code (B. Paassen et al., Bielefeld University)
http://github.com/MrNuggelz/sklearn-glvq
http://techfak.uni-bielefeld.de/~bpaassen/glvq.zip
Java plugin for WEKA (M. Kaden et al., Hochschule Mittweida)
https://github.com/JonStargaryen/gmlvq/blob/master/README.md

52. WISMAL 2020 52
Questions ?
?