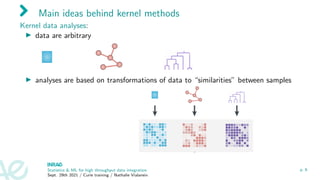
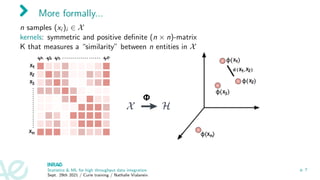
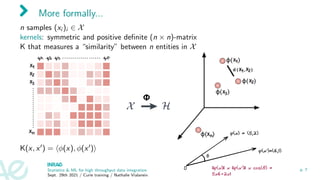
The document presents an overview of kernel methods and their application in exploratory analysis and multi-omics integration, focusing on the importance of kernels for data integration and improving interpretability. It discusses various key concepts, including a formal definition of kernels, examples of their use in different contexts, and strategies for optimal kernel combination. Additionally, the document addresses challenges related to scaling and feature selection in kernel methods, suggesting techniques for enhancing interpretability and performance.












![Kernel examples
1. Rp observations: Gaussian kernel Kii0 = e−γkxi −xi0 k2
2. nodes of a graph: [Kondor and Lafferty, 2002]
3. sequence kernels (between proteins: spectrum kernel [Jaakkola et al., 2000] (with
HMM), convolution kernel [Saigo et al., 2004]
4. kernel between graphs (used between metabolites based on their fragmentation
trees): [Shen et al., 2014, Brouard et al., 2016]
Statistics & ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 11](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-16-320.jpg)

![Types of data integration methods [Ritchie et al., 2015]
Statistics & ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 13](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-18-320.jpg)


![Multiple kernel (or distance) integration
How to “optimally” combine several kernel datasets?
For kernels K1, . . . , KM obtained on the same n objects, search: Kβ =
PM
m=1 βmKm
with βm ≥ 0 and
P
m βm = 1
I naive approach: K∗ = 1
M
P
m Km
I supervised framework: K∗ =
P
m βmKm with βm ≥ 0 and
P
m βm = 1 with βm
chosen so as to minimize the prediction error [Gönen and Alpaydin, 2011]
Statistics & ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 14](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-21-320.jpg)

![Multiple kernel integration
Ideas of kernel consensus: find a kernel that performs a consensus of all kernels
[Mariette and Villa-Vialaneix, 2018] - R package mixKernel
with consensus based on:
I STATIS [L’Hermier des Plantes, 1976, Lavit et al., 1994]
I criterion that preserves local geometry
Statistics & ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 16](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-23-320.jpg)
![STATIS like framework
Similarities between kernels:
Cmm0 =
hKm, Km0
iF
kKmkF kKm0
kF
=
Trace(KmKm0
)
p
Trace((Km)2)Trace((Km0
)2)
.
(Cmm0 is an extension of the RV-coefficient [Robert and Escoufier, 1976] to the kernel
framework)
maximizev
M
X
m=1
K∗
(v),
Km
kKmkF
F
= v
Cv
for K∗
(v) =
M
X
m=1
vmKm
and v ∈ RM
such that kvk2 = 1.
Solution: first eigenvector of C ⇒ Set β = v
PM
m=1 vm
(consensual kernel).
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 17](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-24-320.jpg)
![A kernel preserving the original topology of the data I
Similarly to [Lin et al., 2010], preserve the local geometry of the data in the feature
space.
Proxy of the local geometry
Km
−→ Gm
k
| {z }
k−nearest neighbors graph
−→ Am
k
| {z }
adjacency matrix
⇒ W =
P
m I{Am
k 0} or W =
P
m Am
k
Feature space geometry measured by
∆i (β) =
*
φ∗
β(xi ),
φ∗
β(x1)
.
.
.
φ∗
β(xn)
+
=
K∗
β(xi , x1)
.
.
.
K∗
β(xi , xn)
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 18](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-25-320.jpg)
![A kernel preserving the original topology of the data II
Sparse version (quadprog in R)
minimizeβ
N
X
i,j=1
Wij k∆i (β) − ∆j (β)k2
for K∗
β =
M
X
m=1
βmKm
and β ∈ RM
st βm ≥ 0 and
M
X
m=1
βm = 1.
Non sparse version (ADMM optimization) [Boyd et al., 2011]
minimizev
N
X
i,j=1
Wij k∆i (β) − ∆j (β)k2
for K∗
v =
M
X
m=1
vmKm
and v ∈ RM
st vm ≥ 0 and kvk2 = 1.
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 19](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-26-320.jpg)





![Selecting features in kernels
Basic principles (for numerical features only):
I label each feature j with a weight wj ∈ {0, 1} (selected or not)
I new kernel: Kw(xi , xi0 ) = K(w · xi , w · xi0 )
I find the best features to optimize a quality criterion (relaxation of wj ≥ 0)
Examples:
I supervised framework: learn w to compute a kernel Kw
x best to predict Y ∈ R
[Allen, 2013, Grandvalet and Canu, 2002]
I extended to unsupervised (exploratory) learning and arbitrary outputs (kernel
outputs, including multiple output regression) (non-convex and non-smooth
optimization solved with proximal gradient descent) [Brouard et al., 2021] and in
mixKernel
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 23](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-32-320.jpg)
![UKFS performances
lapl SPEC MCFS NDFS UDFS Autoenc. UKFS
“Carcinom” (n = 174, p = 9 182)
ACC 164.02 106.52 184.17 200.88 138.48 143.13 206.55
COR 28.14 30.75 29.56 27.49 30.30 33.18 24.75
CPU 0.25 2.47 11.69 6,162 99,138 4 days 326
“Glioma” (n = 50, p = 4 434)
ACC 166.31 140.72 172.78 147.77 147.50 132.76 178.57
COR 81.70 70.70 76.43 68.02 72.33 45.96 52.14
CPU 0.02 0.63 1.05 368 2,636 ∼ 12h 23.74
“Koren” (n = 43, p = 980)
ACC 172.90 225.25 233.94 263.04 263.48 239.76 242.39
COR 48.18 52.34 49.94 48.48 48.69 32.60 47.77
CPU 0.01 0.07 1.11 5.88 9.70 ∼ 30 min 10.69
[Brouard et al., 2021]
I non redundant features
I can incorporate information on relations between variables
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 24](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-33-320.jpg)
![KOKFS illustration
Used with covid19 dataset from [Haug et al., 2020]:
I inputs: 46 government measures (0/1 encoding)
I outputs: R time series (with a kernel based on Fréchet distances)
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 25](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-34-320.jpg)
![KOKFS illustration
Used with covid19 dataset from [Haug et al., 2020]:
I inputs: 46 government measures (0/1 encoding)
I outputs: R time series (with a kernel based on Fréchet distances)
More important measures:
Increase In Medical Supplies And Equipment
Border Health Check
Public Transport Restriction
The Government Provides Assistance To Vulnerable Populations
Individual Movement Restrictions
Increase Availability Of Ppe
Activate Case Notification
Border Restriction
Measures To Ensure Security Of Supply
Port And Ship Restriction
Activate Or Establish Emergency Response
Statistics ML for high throughput data integration
Sept. 29th 2021 / Curie training / Nathalie Vialaneix
p. 25](https://image.slidesharecdn.com/vialaneixcurietraining2021-09-29-210930061154/85/Kernel-methods-and-variable-selection-for-exploratory-analysis-and-multi-omics-integration-35-320.jpg)




