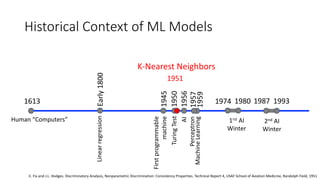
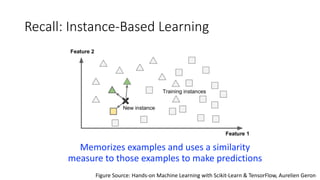
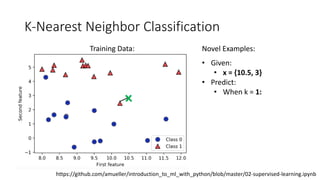
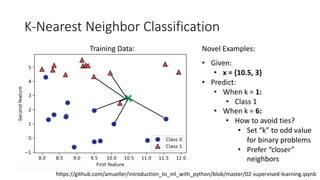
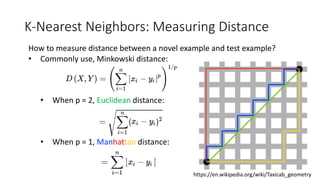
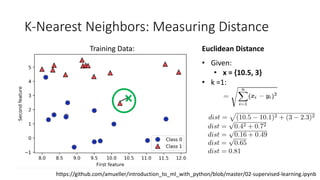
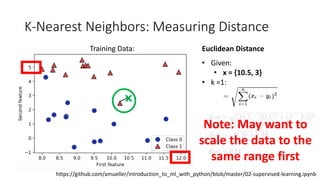
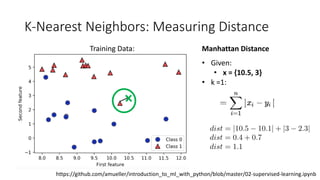
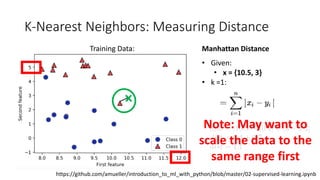
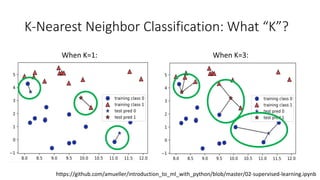
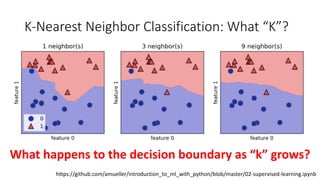
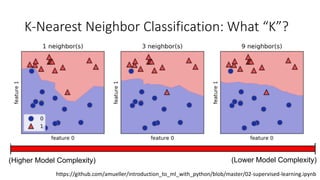
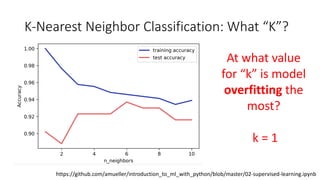
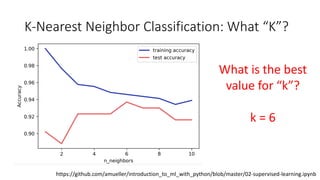
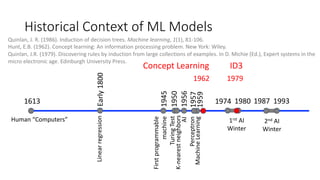
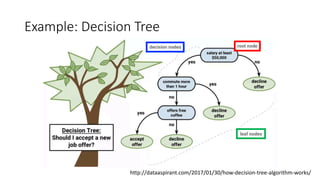
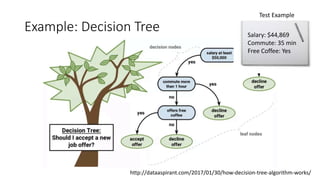
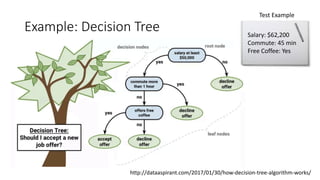
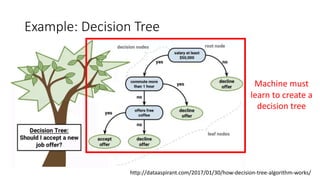
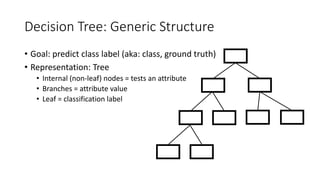
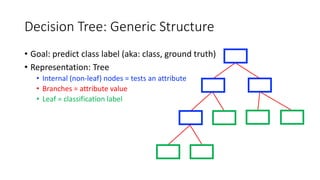
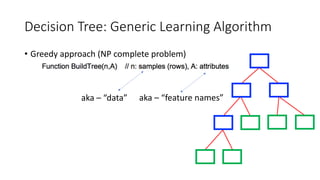
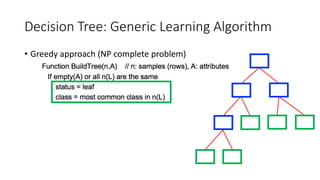
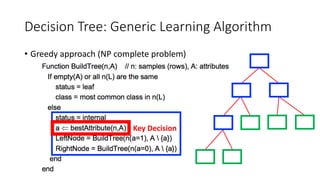
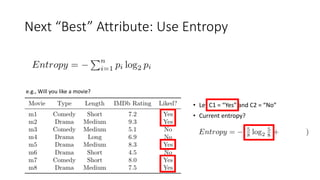
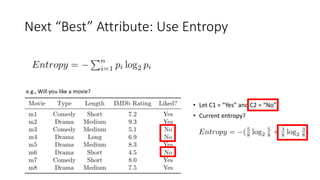
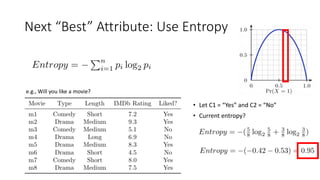
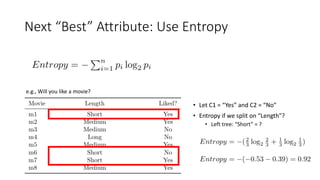
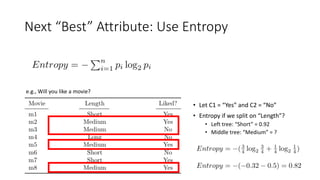
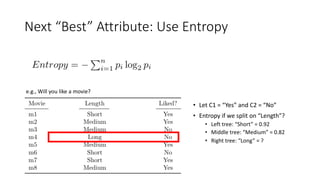
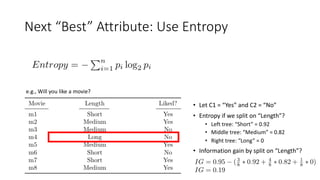
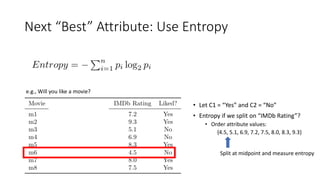
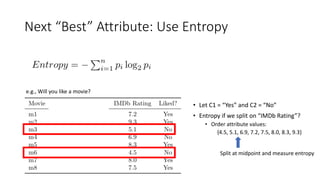
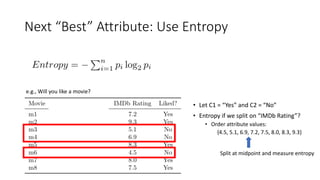
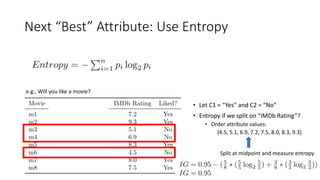
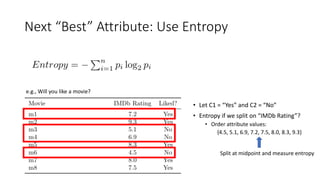
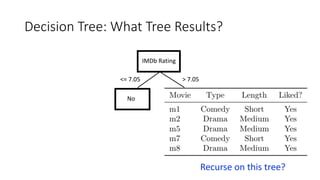
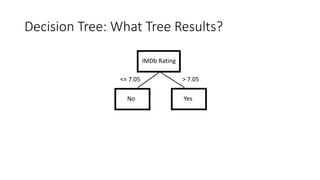
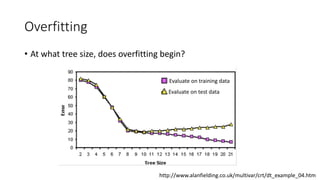
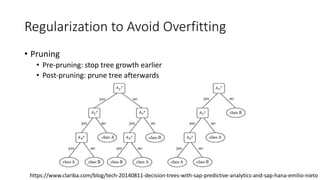
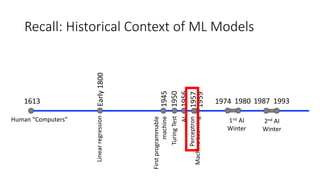
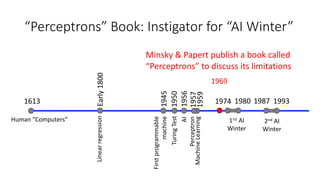
The document covers topics in machine learning, specifically focusing on multiclass classification, nearest neighbor classification, and decision tree classification. It discusses the evolution and historical context of machine learning models, including challenges like the XOR problem and the need for non-linear models. The document also elaborates on evaluation methods, training data organization, and the strengths and weaknesses of k-nearest neighbors (KNN) methods.

1. Nearest Neighbor, Decision Tree
Danna Gurari
University of Texas at Austin
Spring 2021
https://www.ischool.utexas.edu/~dannag/Courses/IntroToMachineLearning/CourseContent.html

2. Review
• Last week:
• Binary classification applications
• Evaluating classification models
• Biological neurons: inspiration
• Artificial neurons: Perceptron & Adaline
• Gradient descent
• Assignments (Canvas)
• Lab assignment 1 due tonight
• Problem set 3 due next week
• Questions?

3. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric models

4. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric models

5. Today’s Focus: Multiclass Classification
Predict 3+ classes

6. Multiclass Classification: Cancer Diagnosis
https://news.stanford.edu/2017/01/25/artificial-intelligence-used-identify-skin-cancer/
https://www.nature.com/articles/nature21056
Doctor-level performance in recognizing 2,032 diseases

7. Multiclass Classification: Face Recognition
Security
https://www.anyvision.co/
Visual assistance for people
with vision impairments
Social media

8. Multiclass Classification: Shopping
Camfind (https://venturebeat.com/2014/09/24/camfind-app-
brings-accurate-visual-search-to-google-glass-exclusive/)

9. Multiclass Classification: Song Recognition
https://gbksoft.com/blog/how-to-make-a-shazam-like-app/

10. Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
Input:
Label: Cat Dog Person

11. 1. Split data into a “training set” and “ ”
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
Training Data Test Data
Input:
Label: Cat Dog Person

12. Training Data Test Data
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
Input:
Label: Cat Dog
2. Train model on “training set” to try to minimize prediction error on it
Person

13. Prediction Model
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
3. Apply trained model on “ ” to measure generalization error
? ? ?
Input:
Label:

14. Prediction Model
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
3. Apply trained model on “ ” to measure generalization error
Cat ? ?
Input:
Label:

15. Prediction Model
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
3. Apply trained model on “ ” to measure generalization error
Cat Giraffe ?
Input:
Label:

16. Prediction Model
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
3. Apply trained model on “ ” to measure generalization error
Cat Giraffe Person
Input:
Label:

17. Prediction Model
Goal: Design Models that Generalize Well to
New, Previously Unseen Examples
3. Apply trained model on “ ” to measure generalization error
Cat Giraffe Person
Input:
Label:
Cat Pumpkin
Human Annotated Label: Person

18. • Accuracy: percentage correct
• Precision:
• Recall:
Evaluation Methods
• Confusion matrix; e.g.,
http://gabrielelanaro.github.io/blog/2016/0
2/03/multiclass-evaluation-measures.html

19. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric models

20. Recall: Historical Context of ML Models
1613
Human “Computers”
1945
First
programmable
machine
Turing
Test
1959
Machine
Learning
1956
Early
1800 1974 1980 1987 1993
1rst AI
Winter
2nd AI
Winter
Linear
regression
1957
Perceptron
1950
AI

21. Recall: Vision for Perceptron
Frank Rosenblatt
(Psychologist)
“[The perceptron is] the embryo of an
electronic computer that [the Navy] expects
will be able to walk, talk, see, write,
reproduce itself and be conscious of its
existence…. [It] is expected to be finished in
about a year at a cost of $100,000.”
1958 New York Times article: https://www.nytimes.com/1958/07/08/archives/new-
navy-device-learns-by-doing-psychologist-shows-embryo-of.html
https://en.wikipedia.org/wiki/Frank_Rosenblatt

22. “Perceptrons” Book: Instigator for “AI Winter”
1613
Human “Computers”
1945
First
programmable
machine
Turing
Test
1959
Machine
Learning
1956
Early
1800 1974 1980 1987 1993
1rst AI
Winter
2nd AI
Winter
Linear
regression
1957
Perceptron
1950
AI
1969
Minsky & Papert publish a book called
“Perceptrons” to discuss its limitations

23. Perceptron Limitation: XOR Problem
XOR = “Exclusive Or”
- Input: two binary values x1 and x2
- Output:
- 1, when exactly one input equals 1
- 0, otherwise
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
?
?
?
?

24. Perceptron Limitation: XOR Problem
XOR = “Exclusive Or”
- Input: two binary values x1 and x2
- Output:
- 1, when exactly one input equals 1
- 0, otherwise
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
?
?
?
?

25. Perceptron Limitation: XOR Problem
XOR = “Exclusive Or”
- Input: two binary values x1 and x2
- Output:
- 1, when exactly one input equals 1
- 0, otherwise
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
0
?
?
?

26. Perceptron Limitation: XOR Problem
XOR = “Exclusive Or”
- Input: two binary values x1 and x2
- Output:
- 1, when exactly one input equals 1
- 0, otherwise
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
0
1
?
?

27. Perceptron Limitation: XOR Problem
XOR = “Exclusive Or”
- Input: two binary values x1 and x2
- Output:
- 1, when exactly one input equals 1
- 0, otherwise
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
0
1
1
?

28. Perceptron Limitation: XOR Problem
XOR = “Exclusive Or”
- Input: two binary values x1 and x2
- Output:
- 1, when exactly one input equals 1
- 0, otherwise
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
0
1
1
0

29. Perceptron Limitation: XOR Problem
x1 x2 x1 XOR x2
0 0
0 1
1 0
1 1
0
1
1
0
How to separate 1s from 0s with a perceptron (linear function)?

30. Perceptron Limitation: XOR Problem
Frank Rosenblatt
(Psychologist)
“[The perceptron is] the embryo of an
electronic computer that [the Navy] expects
will be able to walk, talk, see, write,
reproduce itself and be conscious of its
existence…. [It] is expected to be finished in
about a year at a cost of $100,000.”
1958 New York Times article: https://www.nytimes.com/1958/07/08/archives/new-
navy-device-learns-by-doing-psychologist-shows-embryo-of.html
How can a machine be “conscious”
when it can’t solve the XOR problem?

31. How to Overcome Limitation?
Non-linear models: e.g.,
• Linear regression: perform non-linear transformation of input features
• K-nearest neighbors
• Decision trees
• And many more to follow…

32. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric model

33. Historical Context of ML Models
1613
Human “Computers”
1945
First
programmable
machine
Turing
Test
1959
Machine
Learning
1956
Early
1800 1974 1980 1987 1993
1rst AI
Winter
2nd AI
Winter
Linear
regression
1957
Perceptron
1950
AI
1951
K-Nearest Neighbors
E. Fix and J.L. Hodges. Discriminatory Analysis, Nonparametric Discrimination: Consistency Properties. Technical Report 4, USAF School of Aviation Medicine, Randolph Field, 1951

34. Recall: Instance-Based Learning
Memorizes examples and uses a similarity
measure to those examples to make predictions
Figure Source: Hands-on Machine Learning with Scikit-Learn & TensorFlow, Aurelien Geron

35. e.g., Predict What Scene The Image Shows
Input Output
Kitchen
Database Search

36. Input:
Label:
1. Create Large Database
e.g., Predict What Scene The Image Shows
Kitchen Coast
Store

37. e.g., Predict What Scene The Image Shows
2. Organize Database so Visually Similar Examples Neighbor Each Other
Adapted from slides by Antonio Torralba

38. 3. Predict Class Using Label of Most Similar Example(s) in the Database
Input:
Label: ?
Adapted from slides by Antonio Torralba
e.g., Predict What Scene The Image Shows

39. 3. Predict Class Using Label of Most Similar Example(s) in the Database
e.g., Predict What Scene The Image Shows
Input:
Label: Cathedral
Adapted from slides by Antonio Torralba

40. 3. Predict Class Using Label of Most Similar Example(s) in the Database
e.g., Predict What Scene The Image Shows
Input:
Label: ?
Adapted from slides by Antonio Torralba

41. 3. Predict Class Using Label of Most Similar Example(s) in the Database
e.g., Predict What Scene The Image Shows
Input:
Label: Highway
Adapted from slides by Antonio Torralba

42. K-Nearest Neighbor Classification
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb
Training Data:
• Given:
• x = {10.5, 3}
• Predict:
• When k = 1:
Novel Examples:

43. K-Nearest Neighbor Classification
Training Data:
• Given:
• x = {10.5, 3}
• Predict:
• When k = 1:
• Class 1
• When k = 6:
• How to avoid ties?
• Set “k” to odd value
for binary problems
• Prefer “closer”
neighbors
Novel Examples:
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

44. K-Nearest Neighbors: Measuring Distance
How to measure distance between a novel example and test example?
• Commonly use, Minkowski distance:
• When p = 2, Euclidean distance:
• When p = 1, Manhattan distance:
https://en.wikipedia.org/wiki/Taxicab_geometry

45. K-Nearest Neighbors: Measuring Distance
• Given:
• x = {10.5, 3}
• k =1:
Euclidean Distance
Training Data:
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

46. K-Nearest Neighbors: Measuring Distance
• Given:
• x = {10.5, 3}
• k =1:
Euclidean Distance
Training Data:
Note: May want to
scale the data to the
same range first
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

47. K-Nearest Neighbors: Measuring Distance
• Given:
• x = {10.5, 3}
• k =1:
Manhattan Distance
Training Data:
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

48. K-Nearest Neighbors: Measuring Distance
• Given:
• x = {10.5, 3}
• k =1:
Manhattan Distance
Training Data:
Note: May want to
scale the data to the
same range first
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

49. K-Nearest Neighbors: Measuring Distance
How to measure distance for novel categorical test data?
• e.g., Train = blue
• e.g., Test = blue; identical values so assign distance 0
• e.g., Test = white; different values so assign distance 1
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

50. K-Nearest Neighbor Classification: What “K”?
When K=1: When K=3:
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

51. K-Nearest Neighbor Classification: What “K”?
When K=1: When K=3:
Given that predictions can change with different
values of “k”, what value of “k” should one use?
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

52. K-Nearest Neighbor Classification: What “K”?
What happens to the decision boundary as “k” grows?
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

53. K-Nearest Neighbor Classification: What “K”?
What happens when “k” equals the training data size?
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

54. K-Nearest Neighbor Classification: What “K”?
(Higher Model Complexity) (Lower Model Complexity)
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

55. K-Nearest Neighbor Classification: What “K”?
At what value
for “k” is model
overfitting the
most?
k = 1
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

56. K-Nearest Neighbor Classification: What “K”?
What is the best
value for “k”?
k = 6
https://github.com/amueller/introduction_to_ml_with_python/blob/master/02-supervised-learning.ipynb

57. K-Nearest Neighbor: How to Use to Predict
More than Two Classes?
• Tally number of examples belonging to each class and again choose
the majority vote winners

58. What are Strengths of KNN?
• Adapts as new data is added
• Training is relatively fast
• Easy to understand

59. What are Weaknesses of KNN?
• For large datasets, requires large storage space
• For large datasets, this approach can be very slow or infeasible
• Note: can improve speed with efficient data structures such as KD-trees
• Vulnerable to noisy/irrelevant examples
• Sensitive to imbalanced datasets where more frequent class will
dominate majority voting

60. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric models

61. Historical Context of ML Models
1613
Human “Computers”
1945
First
programmable
machine
Turing
Test
1959
Machine
Learning
1956
Early
1800 1974 1980 1987 1993
1rst AI
Winter
2nd AI
Winter
Linear
regression
1957
Perceptron
1950
AI
Quinlan, J. R. (1986). Induction of decision trees. Machine learning, 1(1), 81-106.
Hunt, E.B. (1962). Concept learning: An information processing problem. New York: Wiley.
Quinlan, J.R. (1979). Discovering rules by induction from large collections of examples. In D. Michie (Ed.), Expert systems in the
micro electronic age. Edinburgh University Press.
K-nearest
neighbors
1962
Concept Learning
1979
ID3

62. Example: Decision Tree
http://dataaspirant.com/2017/01/30/how-decision-tree-algorithm-works/

63. Example: Decision Tree
http://dataaspirant.com/2017/01/30/how-decision-tree-algorithm-works/
Test Example
Salary: $44,869
Commute: 35 min
Free Coffee: Yes

64. Example: Decision Tree
http://dataaspirant.com/2017/01/30/how-decision-tree-algorithm-works/
Test Example
Salary: $62,200
Commute: 45 min
Free Coffee: Yes

65. Example: Decision Tree
http://dataaspirant.com/2017/01/30/how-decision-tree-algorithm-works/
Machine must
learn to create a
decision tree

66. Decision Tree: Generic Structure
• Goal: predict class label (aka: class, ground truth)
• Representation: Tree
• Internal (non-leaf) nodes = tests an attribute
• Branches = attribute value
• Leaf = classification label

67. Decision Tree: Generic Structure
• Goal: predict class label (aka: class, ground truth)
• Representation: Tree
• Internal (non-leaf) nodes = tests an attribute
• Branches = attribute value
• Leaf = classification label

68. Decision Tree: Generic Structure
• Goal: predict class label
• Representation: Tree
• Internal (non-leaf) nodes = tests an attribute
• Branches = attribute value
• Leaf = classification label
How can a machine learn a decision tree?

69. Decision Tree: Generic Learning Algorithm
• Greedy approach (NP complete problem)
aka – “data” aka – “feature names”

70. Decision Tree: Generic Learning Algorithm
• Greedy approach (NP complete problem)

71. Decision Tree: Generic Learning Algorithm
• Greedy approach (NP complete problem)
Key Decision

72. Next “Best” Attribute: Use Entropy
Number of classes
Fraction of examples belonging to class i
Encodes in bits
In a binary setting,
• Entropy is 0 when fraction of examples belonging to a class is 0 or 1
• Entropy is 1 when fraction of examples belonging to each class is 0.5
https://www.logcalculator.net/log-2

73. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Current entropy?

74. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Current entropy?

75. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Current entropy?

76. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Type”?
• Left tree: “Comedy” = ?

77. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Type”?
• Left tree: “Comedy” = ?

78. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Type”?
• Left tree: “Comedy” = 0.92
• Right tree: “Drama” = ?

79. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Type”?
• Left tree: “Comedy” = 0.92
• Right tree: “Drama” = ?

80. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Type”?
• Left tree: “Comedy” = 0.92
• Right tree: “Drama” = 0.97
• Information gain by split on “Type”?

81. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Length”?
• Left tree: “Short” = ?

82. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Length”?
• Left tree: “Short” = 0.92
• Middle tree: “Medium” = ?

83. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Length”?
• Left tree: “Short” = 0.92
• Middle tree: “Medium” = 0.82
• Right tree: “Long” = ?

84. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “Length”?
• Left tree: “Short” = 0.92
• Middle tree: “Medium” = 0.82
• Right tree: “Long” = 0
• Information gain by split on “Length”?

85. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “IMDb Rating”?
• Order attribute values:
{4.5, 5.1, 6.9, 7.2, 7.5, 8.0, 8.3, 9.3}
Split at midpoint and measure entropy

86. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “IMDb Rating”?
• Order attribute values:
{4.5, 5.1, 6.9, 7.2, 7.5, 8.0, 8.3, 9.3}
Split at midpoint and measure entropy

87. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “IMDb Rating”?
• Order attribute values:
{4.5, 5.1, 6.9, 7.2, 7.5, 8.0, 8.3, 9.3}
Split at midpoint and measure entropy

88. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “IMDb Rating”?
• Order attribute values:
{4.5, 5.1, 6.9, 7.2, 7.5, 8.0, 8.3, 9.3}
Split at midpoint and measure entropy

89. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “IMDb Rating”?
• Order attribute values:
{4.5, 5.1, 6.9, 7.2, 7.5, 8.0, 8.3, 9.3}
Split at midpoint and measure entropy

90. Next “Best” Attribute: Use Entropy
e.g., Will you like a movie?
• Let C1 = “Yes” and C2 = “No”
• Entropy if we split on “IMDb Rating”?
• Order attribute values:
{4.5, 5.1, 6.9, 7.2, 7.5, 8.0, 8.3, 9.3}
Split at midpoint and measure entropy

91. Decision Tree: What is Our First Split?
• Greedy approach (NP complete problem)
IG = 0 IG = 0.19 IG = 0.95

92. Decision Tree: What Tree Results?
IMDb Rating
<= 7.05 > 7.05
Recurse on this tree?

93. Decision Tree: What Tree Results?
No
Recurse on this tree?
IMDb Rating
<= 7.05 > 7.05

94. Decision Tree: What Tree Results?
No Yes
IMDb Rating
<= 7.05 > 7.05

95. Decision Tree: Generic Learning Algorithm
• Greedy approach (NP complete problem)
Key Decision
• Entropy (maximize information gain)
• Gini Index (used in CART algorithm)
• Gain ratio (used in C4.5 algorithm)
• Mean squared error
• …

96. Overfitting
• At what tree size, does overfitting begin?
http://www.alanfielding.co.uk/multivar/crt/dt_example_04.htm
Evaluate on training data
Evaluate on test data

97. Regularization to Avoid Overfitting
• Pruning
• Pre-pruning: stop tree growth earlier
• Post-pruning: prune tree afterwards
https://www.clariba.com/blog/tech-20140811-decision-trees-with-sap-predictive-analytics-and-sap-hana-emilio-nieto

98. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric models

99. Machine Learning Goal
• Learn function that maps input features (X) to an output prediction (Y)
Y = f(x)

100. Machine Learning Goal
• Learn function that maps input features (X) to an output prediction (Y)
• Parametric model: has a fixed number of parameters
Y = f(x)

101. Machine Learning Goal
• Learn function that maps input features (X) to an output prediction (Y)
• Parametric model: has a fixed number of parameters
• Non-parametric model: does not specify the number of parameters
Y = f(x)

102. Class Discussion
• For each model, is it parametric or non-parametric?
• Linear regression
• K-nearest neighbors
• What are advantages and disadvantages of parametric models?
• What are advantages and disadvantages of non-parametric models?

103. Today’s Topics
• Multiclass classification applications and evaluating models
• Motivation for new ML era: need non-linear models
• Nearest neighbor classification
• Decision tree classification
• Parametric versus non-parametric models

104. References Used for Today’s Material
• Chapter 3 of Deep Learning book by Goodfellow et al.
• http://www.cs.utoronto.ca/~fidler/teaching/2015/slides/CSC411/06_trees.pdf
• http://www.cs.utoronto.ca/~fidler/teaching/2015/slides/CSC411/tutorial3_CrossVal-DTs.pdf
• http://www.cs.cmu.edu/~epxing/Class/10701/slides/classification15.pdf