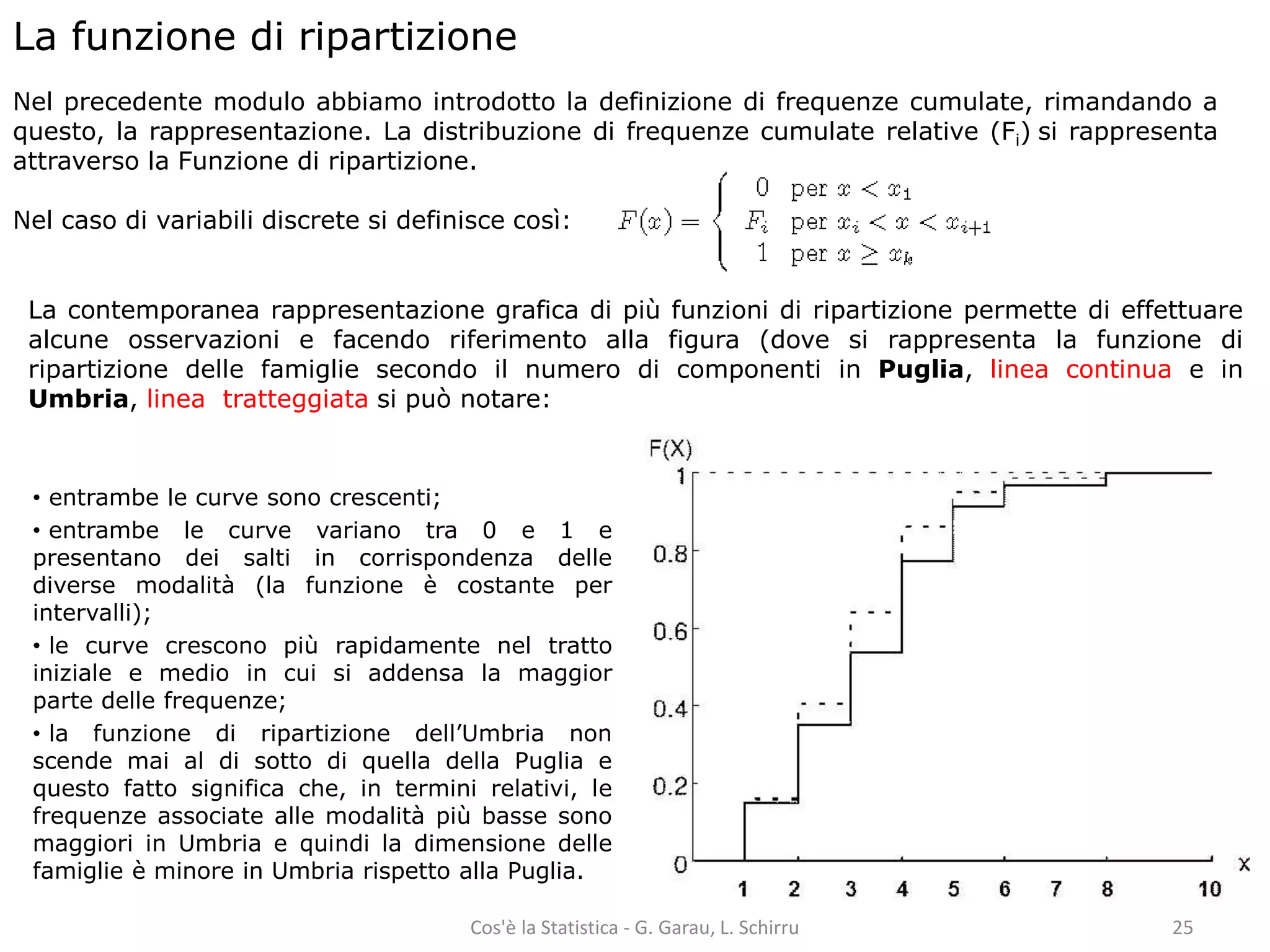
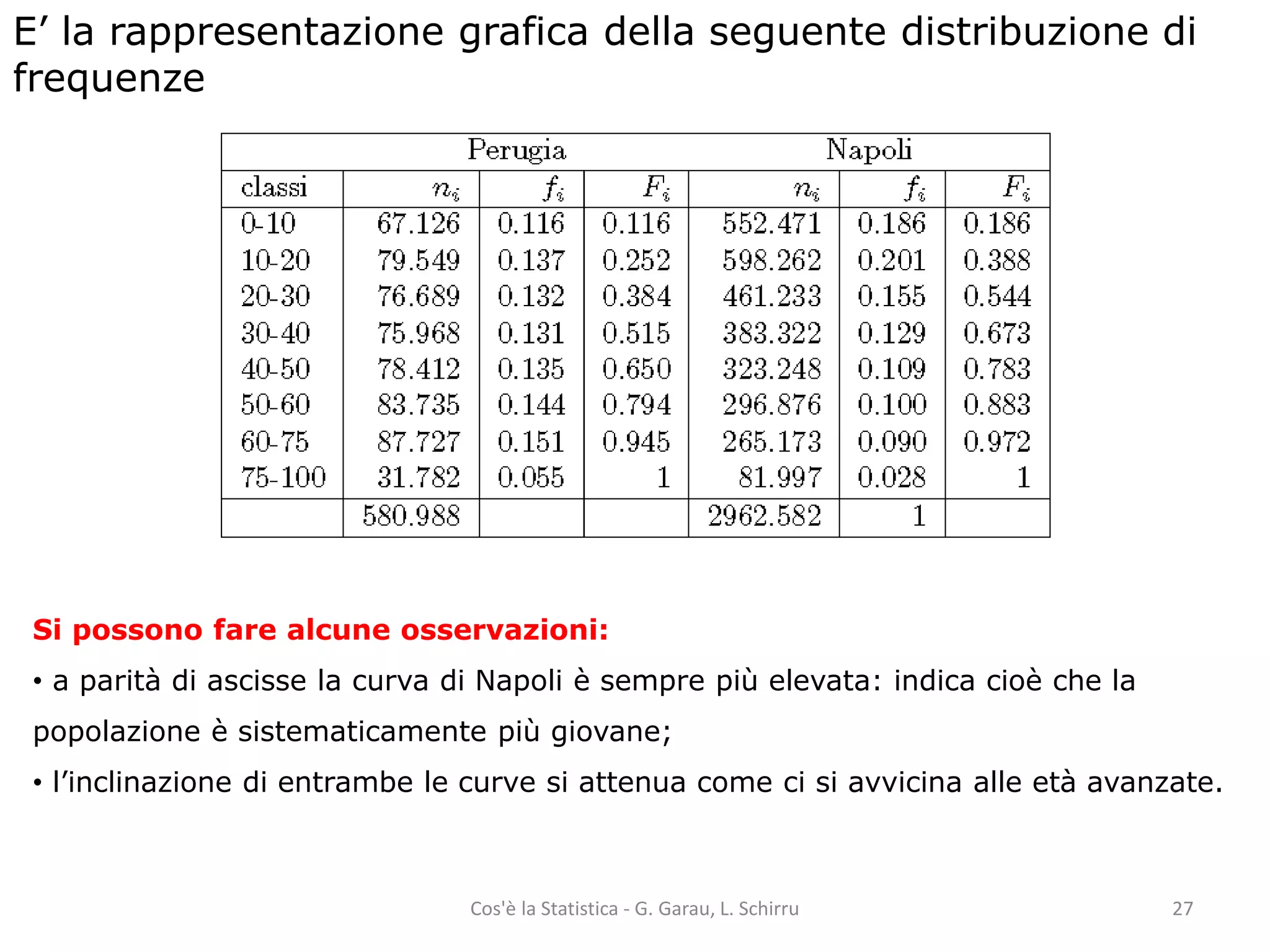
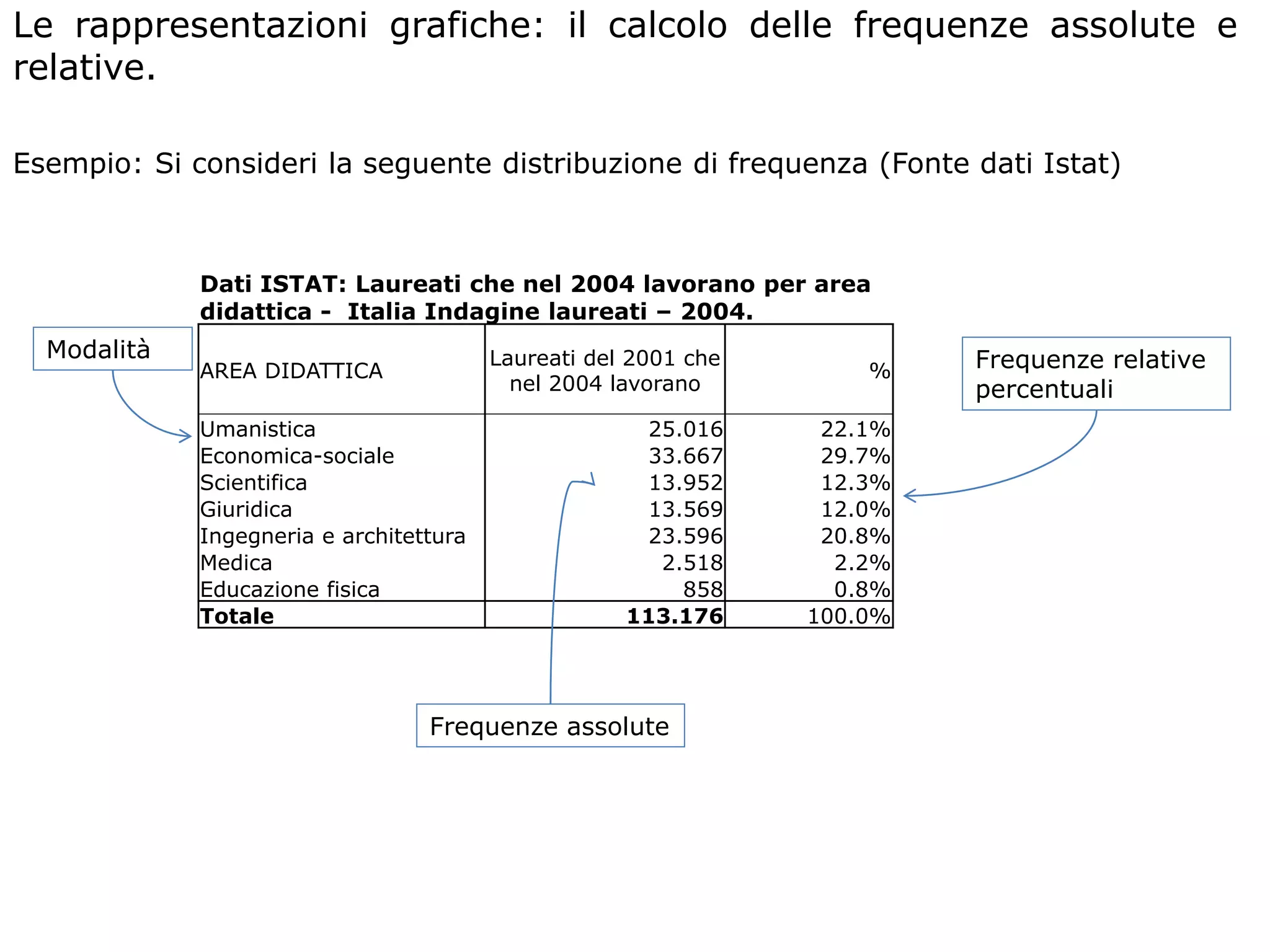
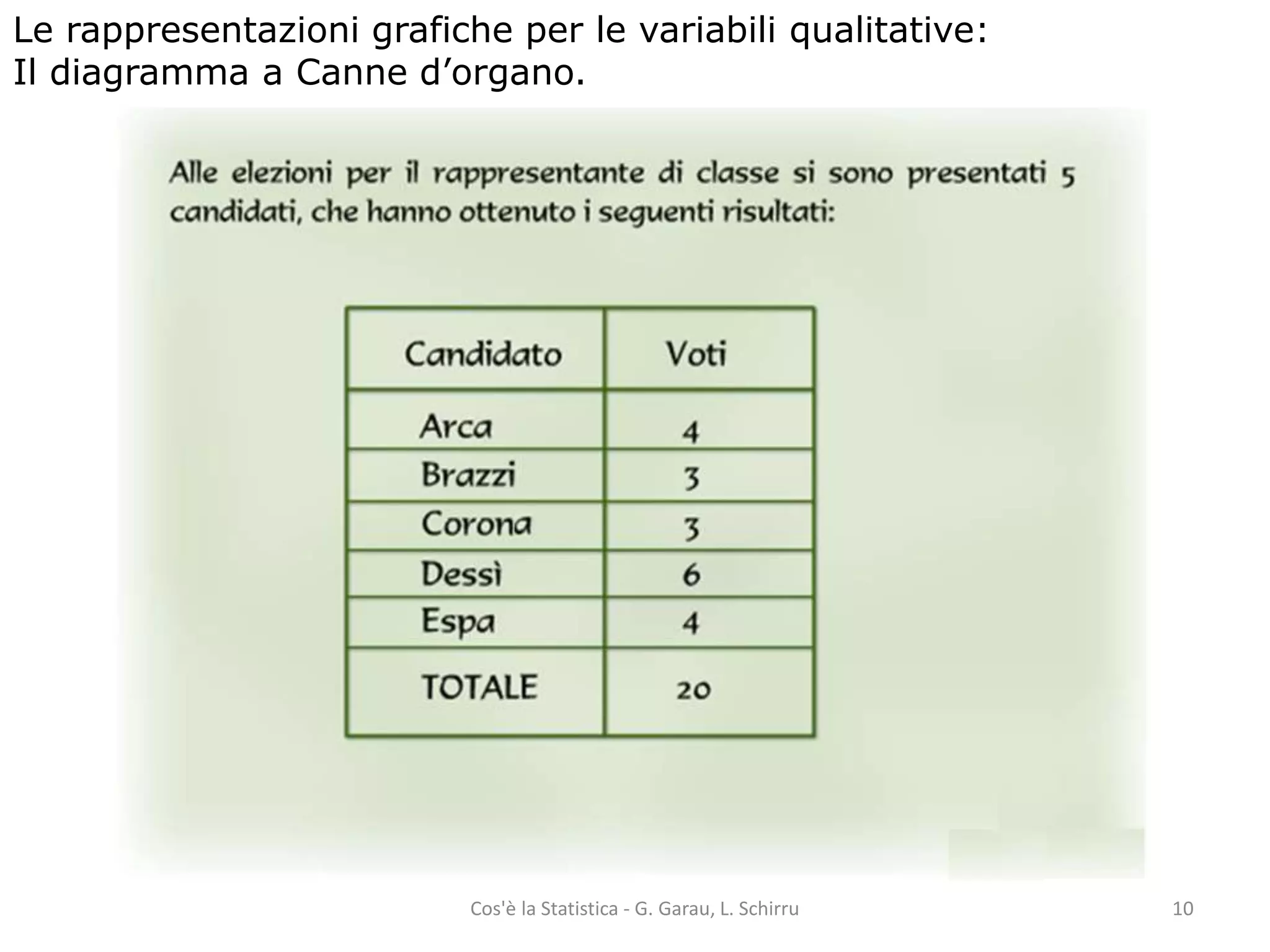
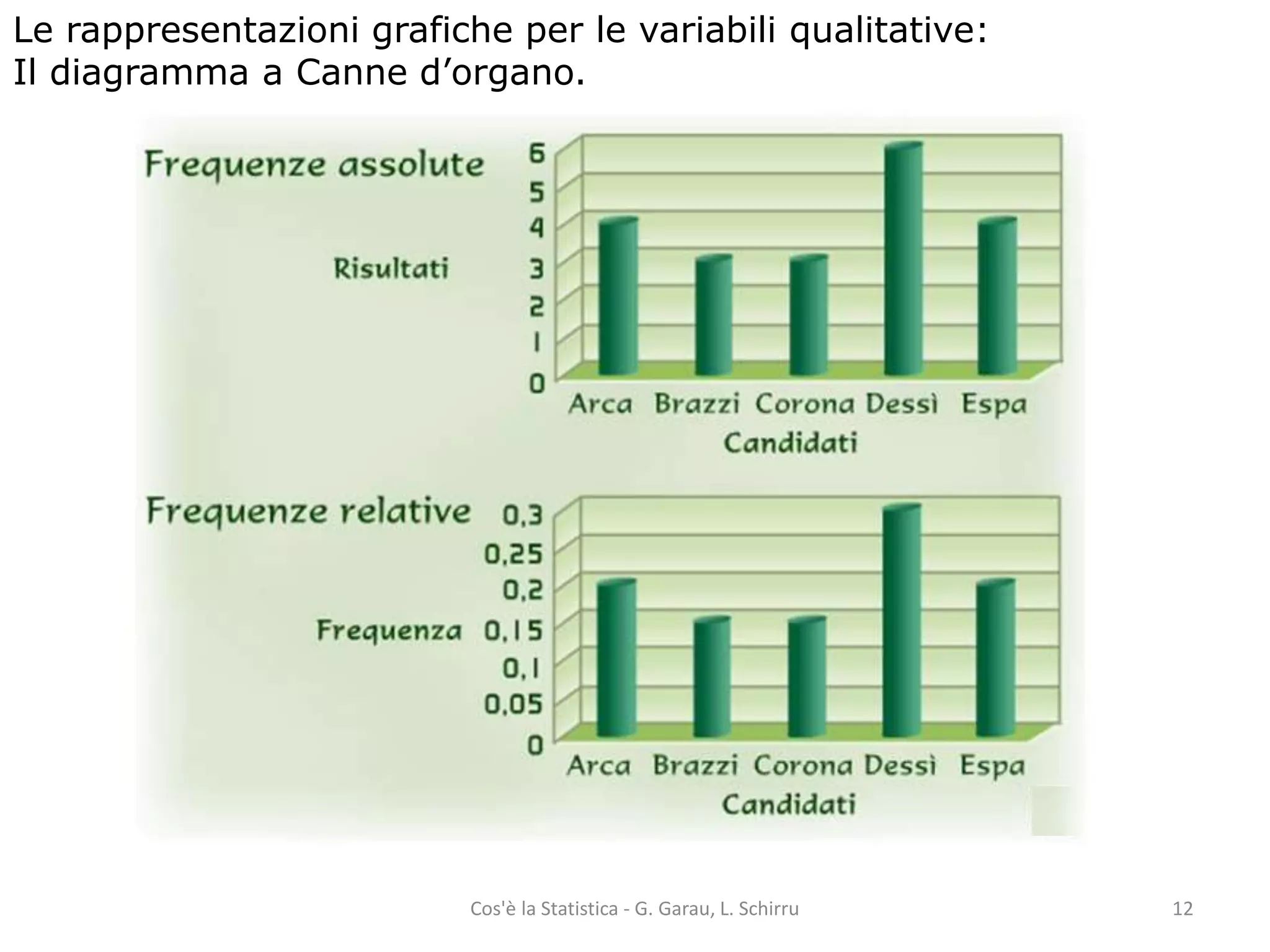
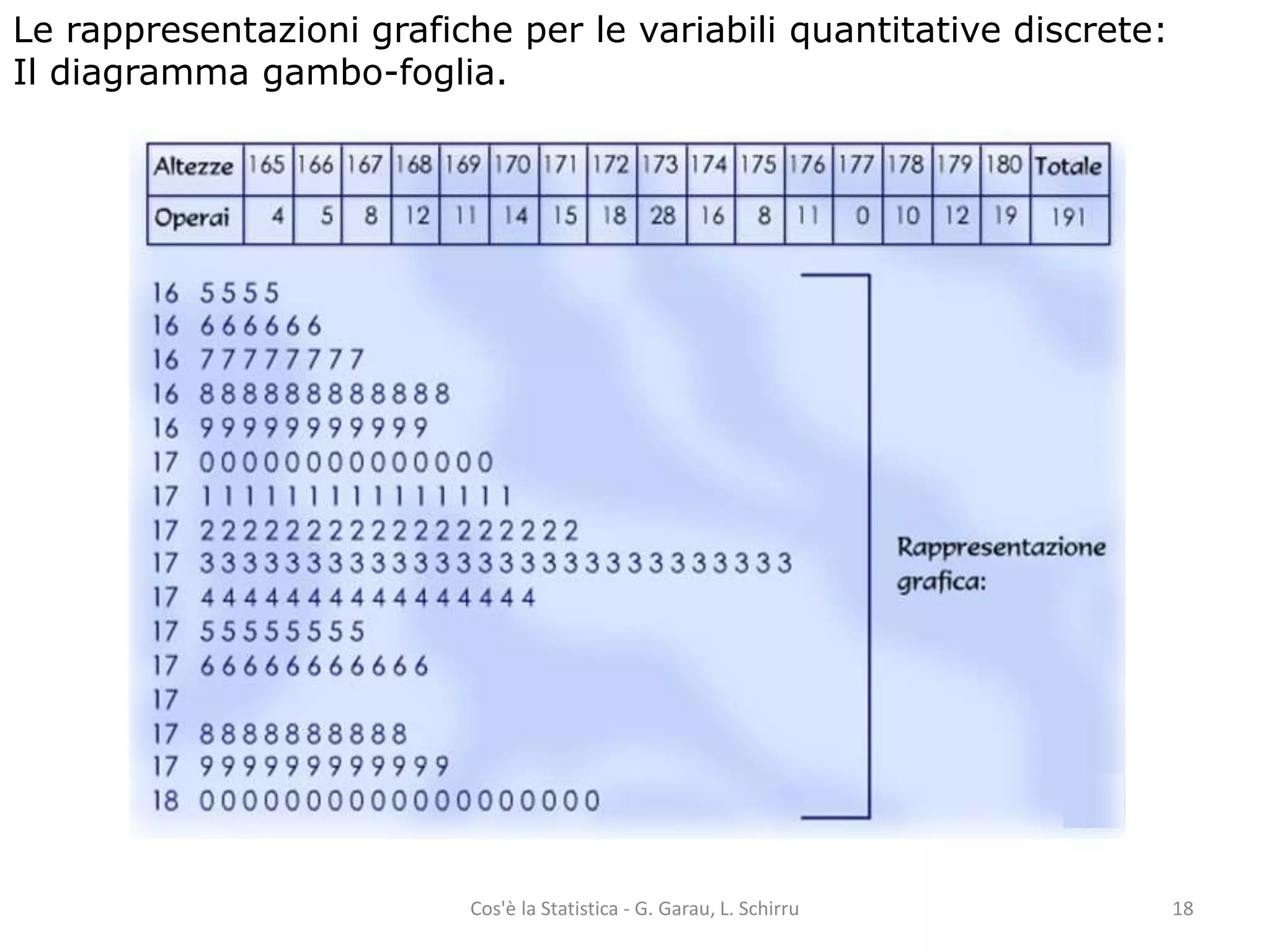
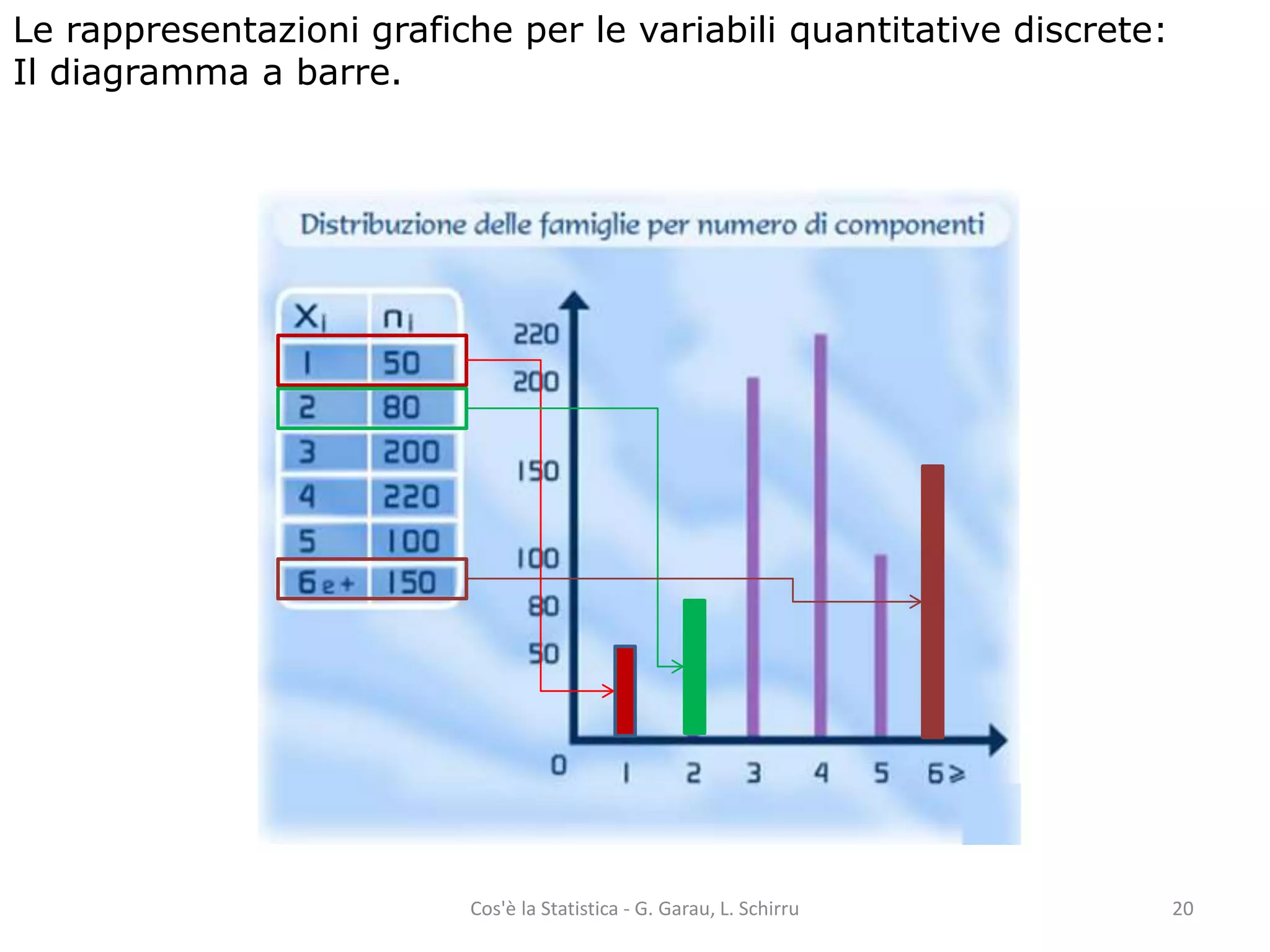
Il documento fornisce una panoramica dei concetti fondamentali della statistica, tra cui la distinzione tra popolazione e campione, unità statistica, caratteri e variabili. Viene spiegato come analizzare e rappresentare graficamente sia variabili qualitative che quantitative, includendo metodi di calcolo delle frequenze e diversi tipi di rappresentazioni grafiche. Infine, si approfondiscono le distribuzioni di frequenza e le funzioni di ripartizione, con esempi pratici di utilizzo.

1. Cos'è la Statistica - G. Garau, L. Schirru 1
Concetti di base
Una popolazione (o universo) è l’insieme di elementi o delle “cose” che si prendono
in considerazione.
Un campione è la porzione della popolazione che si seleziona per l’analisi.
Individuo o unità statistica: è l’unità di base della rilevazione.
Carattere è ciascun tipo di informazione riferita all’unità statistica (es: se gli
studenti che seguono un corso di statistica compongono la popolazione, i caratteri
sono il sesso, l’età, la residenza, il titolo di studio, ecc.).
Una variabile è una caratteristica che cambia da persona a persona (unità
statistica).

2. Concetti di base
variabili
qualitative
quantitative
sconnesse
ordinabili
discrete
continue
Colore capelli:
Biondo, moro,
castano
Giudizio:
Sufficiente,
buono, ottimo
Voto: 18,
25, 28, 30
Costo bibita:
0.70, 0.97, 1.25,
2.28, 3.0
Cos'è la Statistica - G. Garau, L. Schirru 2

3. Cosa si può fare con le variabili qualitative e quantitative
• Variabili qualitative: rappresentazioni grafiche,
calcolo di frequenze assolute e relative, indici di
connessione.
• Variabili quantitative: rappresentazioni grafiche,
calcolo di frequenze assolute e relative, funzioni di
ripartizione, indici di posizione, indici di variabilità,
indici di correlazione, regressione, ecc.
Cos'è la Statistica - G. Garau, L. Schirru 3

4. Le rappresentazioni grafiche
variabili
qualitative
quantitative
sconnesse
ordinabili
discrete
continue
Diagramma a Canne d’organo
Diagramma a torta
Sia
Diagramma Gambo - Foglia
Diagramma a barre
Istogramma
Sia
Cos'è la Statistica - G. Garau, L. Schirru 4

5. Le rappresentazioni grafiche: il calcolo delle frequenze assolute e relative.
Per poter costruire delle rappresentazioni grafiche è necessario aver chiare alcune
definizioni
• Frequenze assolute
• Frequenze relative
• Distribuzione di frequenza
• Frequenze cumulate
Frequenza assoluta. Indica il numero delle volte che una determinata modalità compare nel collettivo in esame. Le modalità
si indicano genericamente con xi per i=1,2,…,n
Frequenza relativa. Si definisce frequenza relativa della modalità xi il rapporto tra la frequenza assoluta xi ed il numero
complessivo delle osservazioni N. Le frequenze relative si indicano con fi. La somma di tutte le frequenze relative è sempre
uguale ad 1.
Distribuzione di frequenze. E’ l’insieme delle modalità e delle rispettive frequenze (assolute o relative), organizzato in
forma tabellare.
Frequenza cumulata. A partire da una distribuzione di frequenze, assolute o relative, si definisce la frequenza cumulata j-esima
(assoluta o relativa) come la somma delle frequenze sino alla classe j-esima compresa. L’ultima frequenza cumulata
assoluta è uguale a N, cioè al totale delle osservazioni, mentre l’ultima frequenza cumulata relativa è pari ad uno. La
distribuzione di frequenza cumulata si rappresenta attraverso la Funzione di Ripartizione.

6. Le rappresentazioni grafiche: il calcolo delle frequenze assolute e
relative.
Esempio: Si consideri la seguente distribuzione di frequenza (Fonte dati Istat)
Dati ISTAT: Laureati che nel 2004 lavorano per area
didattica - Italia Indagine laureati – 2004.
AREA DIDATTICA
Laureati del 2001 che
nel 2004 lavorano
%
Umanistica 25.016 22.1%
Economica-sociale 33.667 29.7%
Scientifica 13.952 12.3%
Giuridica 13.569 12.0%
Ingegneria e architettura 23.596 20.8%
Medica 2.518 2.2%
Educazione fisica 858 0.8%
Totale 113.176 100.0%
Modalità
Frequenze assolute
Frequenze relative
percentuali

7. Le rappresentazioni grafiche: il calcolo delle frequenze relative
cumulate.
1° frequenza relativa cumulata
2° frequenza relativa cumulata
ultima frequenza relativa cumulata
La distribuzione di frequenze cumulate si rappresenta con la Funzione di ripartizione
che verrà analizzata nel dettaglio nel prossimo modulo.

8. Le rappresentazioni grafiche: il calcolo delle frequenze cumulate.
Cos'è la Statistica - G. Garau, L. Schirru 8

9. Le rappresentazioni grafiche: il calcolo delle frequenze cumulate.
Cos'è la Statistica - G. Garau, L. Schirru 9

10. Le rappresentazioni grafiche per le variabili qualitative:
Il diagramma a Canne d’organo.
Cos'è la Statistica - G. Garau, L. Schirru 10

11. Le rappresentazioni grafiche per le variabili qualitative:
Il diagramma a Canne d’organo.
Cos'è la Statistica - G. Garau, L. Schirru 11

12. Le rappresentazioni grafiche per le variabili qualitative:
Il diagramma a Canne d’organo.
Cos'è la Statistica - G. Garau, L. Schirru 12

13. Le rappresentazioni grafiche per le variabili qualitative:
Il diagramma a torta.
Cos'è la Statistica - G. Garau, L. Schirru 13

14. Le rappresentazioni grafiche per le variabili qualitative:
Il diagramma a torta.
Cos'è la Statistica - G. Garau, L. Schirru 14

15. Le rappresentazioni grafiche per le variabili qualitative:
Il diagramma a torta.
Cos'è la Statistica - G. Garau, L. Schirru 15

16. Le rappresentazioni grafiche per le variabili quantitative discrete:
Il diagramma gambo-foglia.
L’utilità del diagramma gambo-foglia consiste nella sua immediatezza visiva, che ci consente di
individuare facilmente intorno a quali valori si concentrano le osservazioni.
Il diagramma gambo-foglia si costruisce dividendo ciascuna osservazione nella sua parte
principale (il “gambo” dell’albero) e in quella secondaria (le “foglie” dell’albero).
Cos'è la Statistica - G. Garau, L. Schirru 16
Vediamo un esempio:
Analizziamo i seguenti dati numerici:
Per capire se i dati hanno una struttura la prima operazione da fare è ordinarli:
29, 31, 31, 31, 31, 32, 33, 33, 33, 33, 34, 35, 35, 36, 37, 38, 39, 39, 41, 42, 42, 43, 44, 47, 51
Al fine di rappresentare graficamente la serie ordinata è necessario adottare una codifica, operazione
che consente di costruire il diagramma gambo-foglia. Nel diagramma la codifica è la seguente:
2|9 = 29
3- = intervallo 30 – 34
3+ = intervallo 35 – 39
25 - 29 9
30 - 34 1 1 1 1 2 3 3 3 3 4
35 - 39 5 5 6 7 8 9 9
40 - 44 1 2 2 3 4
45 – 49 7
50 - 54 1
Si può
scrivere
così:
Oppure così
2+ 9
3- 1 1 1 1 2 3 3 3 3 4
3+ 5 5 6 7 8 9 9
4- 1 2 2 3 4
4+ 7
5- 1

17. Le rappresentazioni grafiche per le variabili quantitative discrete:
Il diagramma gambo-foglia.
Cos'è la Statistica - G. Garau, L. Schirru 17

18. Le rappresentazioni grafiche per le variabili quantitative discrete:
Il diagramma gambo-foglia.
Cos'è la Statistica - G. Garau, L. Schirru 18

19. Le rappresentazioni grafiche per le variabili quantitative discrete:
Il diagramma a barre.
Se si ruota di 90° il diagramma gambo-foglia si ottiene un diagramma a barre. Questa
rappresentazione si utilizza quando le osservazioni si presentano con poche modalità.
Nelle ascisse si indicano le modalità e nelle ordinate le frequenze (assolute o relative).
Cos'è la Statistica - G. Garau, L. Schirru 19

20. Le rappresentazioni grafiche per le variabili quantitative discrete:
Il diagramma a barre.
Cos'è la Statistica - G. Garau, L. Schirru 20

21. Le rappresentazioni grafiche per variabili quantitative continue.
L’Istogramma è la rappresentazione grafica dei dati quantitativi discreti, quando
assumono un numero elevato di modalità, e dei dati quantitativi continui.
Per poter essere rappresentati, i dati devono essere opportunamente raggruppati
in classi e riportati in forma tabellare, ottenendo una distribuzione di frequenza
per dati raggruppati.
La caratteristica distintiva dell’Istogramma è che le frequenze delle modalità sono
rappresentate nelle aree invece che nelle ordinate (così come accade nel
diagramma a barre). In ordinata si indicano, invece, le densità di frequenza (o
frequenze per unità di ampiezza).
Nella costruzione della tabella merita una particolare attenzione la scelta del
numero di classi e l’ampiezza di ciascuna di esse.
Cos'è la Statistica - G. Garau, L. Schirru 21

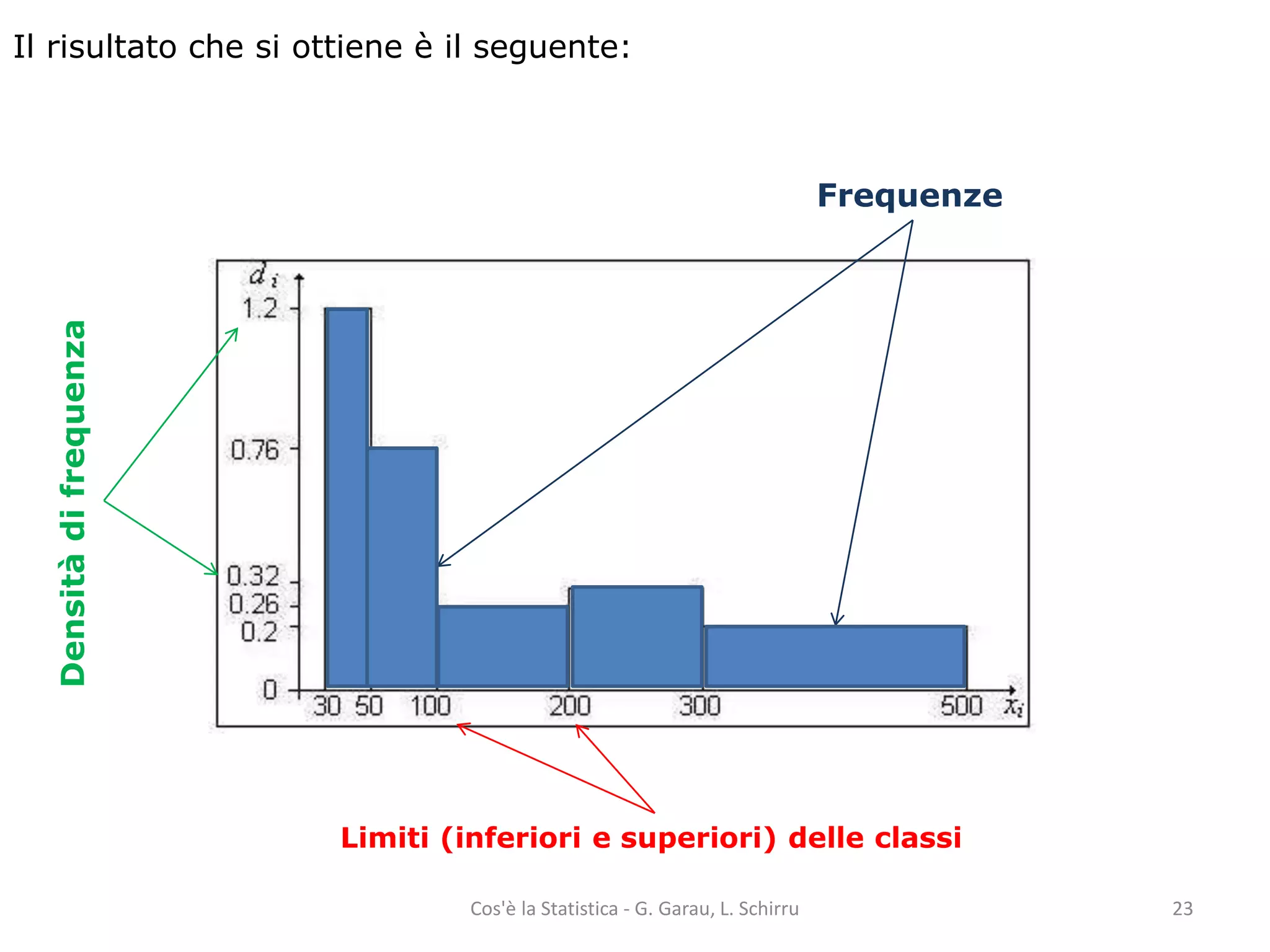
22. Costruiamo l’istogramma relativo alla distribuzione delle aziende per classi
d’investimento (in migliaia di euro), di seguito riportata:
Per rappresentare graficamente (attraverso un istogramma) una distribuzione
in classi occorre:
1. calcolare l’ampiezza di classe (limite superiore meno limite inferiore): [50 - 30], [100 -
50], ecc;
2. calcolare la densità di frequenza. Rapporto tra frequenza e ampiezza di classe;
3. riportare su un sistema di assi cartesiani ortogonali, sull’asse delle ascisse le modalità
(limiti delle classi) e sull’asse delle ordinate le densità di frequenza;
4. costruire per ogni classe i rettangoli aventi come base l’ampiezza di classe e come
altezza la rispettiva densità di frequenza.
Cos'è la Statistica - G. Garau, L. Schirru 22

23. Il risultato che si ottiene è il seguente:
Frequenze
Densità di frequenza
Limiti (inferiori e superiori) delle classi
Cos'è la Statistica - G. Garau, L. Schirru 23

24. Riprendendo l’esempio sulla distribuzione delle altezze di 195 operai (trattato in precedenza)
Scegliendo di formare 5 classi per rispettare la forma originaria della distribuzione, si
suggerisce la seguente ripartizione:
[165 − 168); [168 − 172); [172 − 175); [175 − 177); [177 − 178); [178 − 180].
A cui corrisponde, dopo aver costruito la distribuzione in classi, la seguente
rappresentazione:
Frequenze
24
Cos'è la Statistica - G. Garau, L. Schirru
Densità di frequenza
Valori delle x

25. La funzione di ripartizione
Nel precedente modulo abbiamo introdotto la definizione di frequenze cumulate, rimandando a
questo, la rappresentazione. La distribuzione di frequenze cumulate relative (Fi) si rappresenta
attraverso la Funzione di ripartizione.
Nel caso di variabili discrete si definisce così:
La contemporanea rappresentazione grafica di più funzioni di ripartizione permette di effettuare
alcune osservazioni e facendo riferimento alla figura (dove si rappresenta la funzione di
ripartizione delle famiglie secondo il numero di componenti in Puglia, linea continua e in
Umbria, linea tratteggiata si può notare:
• entrambe le curve sono crescenti;
• entrambe le curve variano tra 0 e 1 e
presentano dei salti in corrispondenza delle
diverse modalità (la funzione è costante per
intervalli);
• le curve crescono più rapidamente nel tratto
iniziale e medio in cui si addensa la maggior
parte delle frequenze;
• la funzione di ripartizione dell’Umbria non
scende mai al di sotto di quella della Puglia e
questo fatto significa che, in termini relativi, le
frequenze associate alle modalità più basse sono
maggiori in Umbria e quindi la dimensione delle
famiglie è minore in Umbria rispetto alla Puglia.
Cos'è la Statistica - G. Garau, L. Schirru 25

26. La funzione di ripartizione per variabili continue
Nel caso di distribuzioni di variabili quantitative ripartite in classi, il valore della
funzione di ripartizione è noto solo in corrispondenza degli estremi delle classi e
facendo l’ipotesi di distribuzione uniforme all’interno delle stesse, la funzione diviene
una spezzata (all’interno della classe si ha un’interpolazione lineare).
Si consideri ora la seguente Funzione di ripartizione per classi di età a Napoli e a Perugia:
Fi
xi
Cos'è la Statistica - G. Garau, L. Schirru 26

27. E’ la rappresentazione grafica della seguente distribuzione di
frequenze
Si possono fare alcune osservazioni:
• a parità di ascisse la curva di Napoli è sempre più elevata: indica cioè che la
popolazione è sistematicamente più giovane;
• l’inclinazione di entrambe le curve si attenua come ci si avvicina alle età avanzate.
Cos'è la Statistica - G. Garau, L. Schirru 27