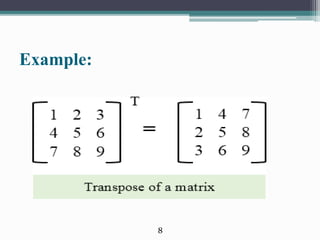
The document presents information on matrices and their applications. It defines what a matrix is as a rectangular arrangement of numbers and expressions in rows and columns. It discusses various operations that can be performed on matrices, including addition, subtraction, multiplication, and finding the transpose. Examples are provided to illustrate these operations. The document also lists some fields where matrices are applied, such as geology, statistics, economics, and animation. It provides examples of how matrices are used in tasks like seismic surveys, data analysis, calculating GDP, and 3D animation.

1. Presented by
Ahmad sajjad
Eman malik
Wasiq nadeem
Saira hameed
Mobeen ali
Presentation on
Matrix and it`s aplication

2. ⦿Definition of a Matrix
⦿ Operations of Matrices
1

3. Matrix (Basic Definitions)
 Aij



kn 



 k1

a ,, a
 
a21 ,, a2n
a11 ,, a1n
A 
Matrices are the rectangular agreement
of numbers, expressions, symbols which
are arranged in columns and rows.
2

4. Operationswith
Matrices
(Sum,Difference)
   
  
   
6 7 0 6 5 1 12 12 1 
3 4 1  1 0 7 2 4 8
If A and B have the same dimensions, then their sum,
A + B, is obtained by adding corresponding entries.
In symbols, (A + B)ij = aij + bij . If A and B have the
same dimensions, then their difference, A − B, is
obtained by subtracting corresponding entries. In
symbols, (A - B)ij = aij - bij .
The matrix 0 whose entries are all zero. Then, for all A
A 0  A
3

5. Operations with Matrices
(Product)
E x a m p le
a n y n  m m a t r i x B , I B  B.
f o r a n y m  n m a t r ix A , A I  A a n d f o r


I d e n t it y m a t r ix I   0








 
 

 n  n
im m j
i 2 2 j
i 1 1 j
m j 
2 j
e B  f D 
 e A  f C
c B  d D 
a B  b D 
 a A  b C
   A B 
f  
 e
 c d .
C D
   c A  d C
 a b 
 a b  a b  . . .  a b .
 b 
 b 
 b1 j
( a i1 a i 2 . . . a im )
 
0 0  1
 
  
1  0


 1 0  0 



IfAhas dimensions k × m and B has dimensions m × n, then the product
AB is defined, and has dimensions k × n. The entry (AB)ij is obtained
by multiplying row i ofAby column j of B, which is done by multiplying
corresponding entries together and then adding the results i.e.,
5

6. 
 
 23 


 23 
13
21 22

a a a
a11 a12 a13
a
a
 a12 a22 
a11 a21 
T
The transpose, AT, of a matrix A is the matrix obtained from A by
writing its rows as columns. IfAis an k×n matrix and B =AT then
B is the n×k matrix with bij = aji. IfAT=A, thenAis symmetric
7

7. Example:
8

8. ⦁ Field of Geology
● Taking seismic surveys
● Plotting graphs & statistics
● Scientific analysis
16

9. ⦿ Field of Statistics & Economics
● Presenting real world data such as People's habit, traits &
survey data
● Calculating GDP
⦿ Field of Animation
● Operating 3D software & Tools
● Performing 3D scaling/Transforming
● Giving reflection, rotation
17

10. ANY QUESTIONS?