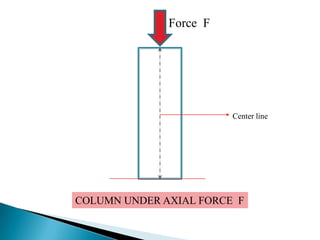
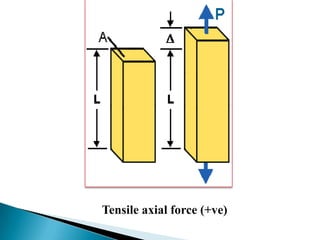
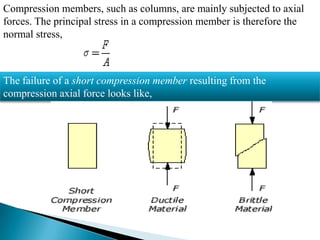
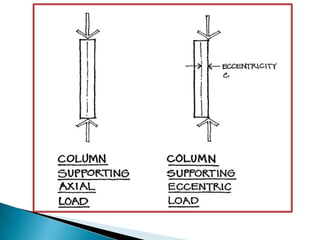
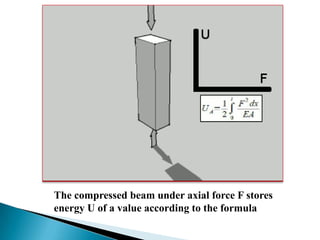
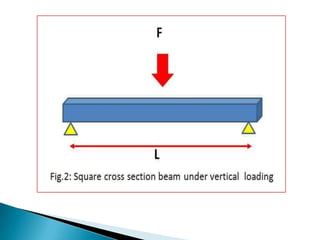
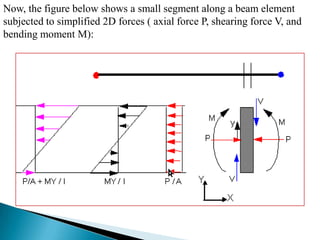
This document summarizes a presentation on axial force given by Md. Shariful Islam to the Department of Civil Engineering at Ahsanullah University of Science & Technology. It defines axial force as a force applied parallel to the centerline of an object. Axial force is determined by factors like width, effective length, and load. It provides examples of compressive and tensile axial forces in columns and beams. The document describes key concepts like concentric and eccentric axial forces, and how axial force relates to stress, strain, and the bending of structural elements.

1. AHSANULLAH UNIVERSITY OF SCIENCE & TECHNOLOGY
Department of Civil Engineering
Prestress Concrete Design Sessional
CE 416
PRESENTED BY
MD. SHARIFUL ISLAM
STUDENT NO: 10.01.03.008
COURSE TEACHERS
Mr. Munshi Galib Muktadir
Ms. Sabreena Nasrin

2. PRESENTATION TOPIC :
AXIAL FORCE

3. PRESENTATION OUTLINE
-Definition
-Unit
-Scope
-Description
-Conclusion

4.  A force
applied parallel to the centerline of an
object.
Axial force evaluates the internal forces that
exist in a structure, often presented by the
characteristics of its dimensions.

5. Force F
Center line
COLUMN UNDER AXIAL FORCE F

7. Axial force is determined by width, effective
length, and load and is measured in kilo
pounds or kips (1,000 pounds of force).

8. SCOPE:

9. Compressive axial force (-ve)

10. Tensile axial force (+ve)

11. Compression members, such as columns, are mainly subjected to axial
forces. The principal stress in a compression member is therefore the
normal stress,
The failure of a short compression member resulting from the
compression axial force looks like,

12. DESCRIPTION

13. 
An axial force is any force that directly acts on the center
axis of an object. These forces are typically stretching
force or compression force, depending on direction.

A prime example of these forces can be seen on
columns within buildings. The column has an axis that
runs through the entire form from top to bottom. The
column is constantly compressed as it supports the
roof of the structure.

14. One of the most important parts of examining axial forces is
the idea of a geometric center.
Geometric center:
This is a point within the boundaries of a solid object that is
the perfect center of the entire mass. It is basically the point at
which the mass of the object is the same in any opposing
direction.
Factors such as density and protruding arms could cause the
geometric center to exist on the surface or even outside of the
form.

15. Concentric:
when the force load is even across the form’s geometric center,
it is concentric.
Eccentric:
when the force load is uneven across the form’s geometric
center, it is eccentric.
 In the column example, the axial force runs through the
geometric center of the form; this makes the force
concentric. A concentric force is stable at rest. When the
axis doesn’t pass through the geometric center, the shape
isn’t stable and the force is eccentric. This typically means
that the form is unable to withstand axial forces while at
rest.

17. The compressed beam under axial force F stores
energy U of a value according to the formula

19. Now, the figure below shows a small segment along a beam element
subjected to simplified 2D forces ( axial force P, shearing force V, and
bending moment M):

20. In a general case 3 forces and 3 moments act on the segment.
Uniform axial stress = P/A (similar to truss elements)
Uniform shearing stress = V/A
The bending moment M causes a bending stress that varies linearly with
the vertical distance y from the neutral axis.
Bending stress (bending in y direction) = My/I
where I is the moment of inertia about the neutral axis.
The bending stress is the largest at the extreme fibers.
In this example, the largest compression occurs at the top fiber and the
largest tension occurs at the extreme bottom fibers.

21. THANK YOU