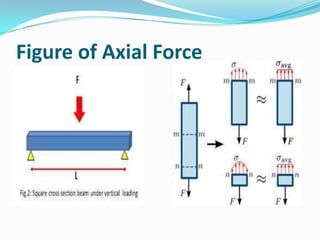
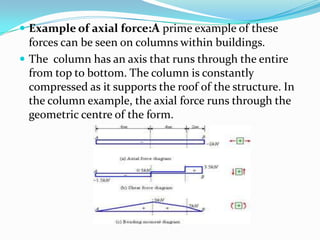
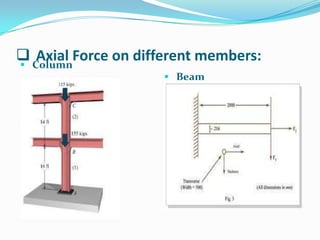
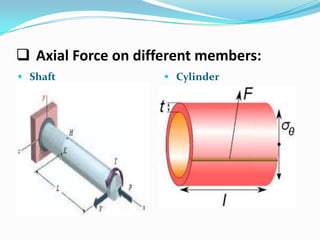
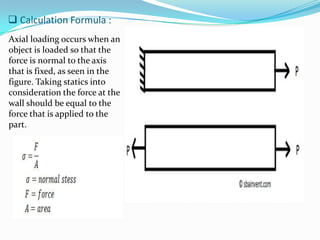
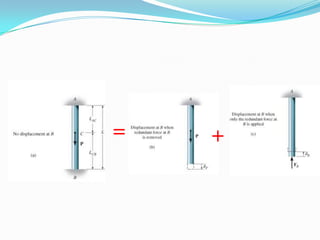
This presentation summarizes axial force and how it relates to structural members. It defines axial force as a force that acts along the longitudinal axis of a member and can put the member in either compression or tension. Eccentric axial loads produce both axial force and bending moment in a member. Examples of structural elements experiencing axial force are given, such as columns supporting a building. Formulas for calculating axial force are presented. The principles of static determinacy, compatibility, and equilibrium are applied to solve an example problem involving axial force in a steel rod.

1. WELCOME
TO MY
PRESENTATION

2. AHSANULLAH UNIVERSITY OF
SCIENCE AND TECHNOLOGY
DEPARTMENT OF CIVIL ENGINEERING
CE-416;PRESTRESS CONCRETE LAB
COURSE TEACHER:MD.GALIB MUKTADIR
PRESENTATION OF AXIAL FORCE
PRESENTED BY
H.M SURUZZAMAN
ID NO:10.01.03.63

3. BACKGROUND: Axial force is a force that tends
to elongate or shorten a member & is normally
measured in pounds. It is a system of internal
forces whose resultant is force that is acting along
the longitudinal axis of a structural member or
assembly.

4.  Axial
force is the compression or
tension force acting in a member. If the
axial force acts through the censored of
the member it is called concentric
loading. If the force is not acting
through the centroid it is called
eccentric loading.
 Eccentric loading produces a moment in the beam as a
result of the load being a distaces away from the
centroid.

5. Learning objectives are:
-Understanding the theory ; it’s limitations, and it’
supplications for design & analysis of axial members
Axial members: Members with length significantly
greater than the largest cross sectional dimension &
with load applied along the longitudinal axis.
-Developing the discipline to draw free body diagrams &
approximate deformed shapes in the
Design & analysis of structures.

6. Nature of axial force:
-These forces are typically stretching force or
compression force, depending on direction.
-Shear forces occupies a similar position to axial
force, but operates perpendicular to the centre axis
of the object.
-When a force is acting directly on the central axis, it
is an axial force. These force will often compress the
axis from either end or stretch the axis in two
opposing directions; as a result the object typically
does not move.

7. Figure of Axial Force

8.  Example of axial force:A prime example of these
forces can be seen on columns within buildings.
 The column has an axis that runs through the entire
from top to bottom. The column is constantly
compressed as it supports the roof of the structure. In
the column example, the axial force runs through the
geometric centre of the form.

9.  ColumnForce on different members:
Axial

 Beam

10.  Axial Force on different members:
 Shaft
 Cylinder

11.  Calculation Formula :
Axial loading occurs when an
object is loaded so that the
force is normal to the axis
that is fixed, as seen in the
figure. Taking statics into
consideration the force at the
wall should be equal to the
force that is applied to the
part.

12. APPROACH OF WORK:
 Used to also solve statically indeterminate problems by
using superposition of the forces acting on the freebody diagram
 First, choose any one of the two supports as
“redundant” and remove its effect on the bar
 Thus, the bar becomes statically determinate
 Apply principle of superposition and solve the
equations simultaneously

13. =
+

14. Compatibility
Choose one of the supports as redundant and write
the equation of compatibility.
Known displacement at redundant support (usually
zero), equated to displacement at support caused
only by external loads acting on the member plus
the displacement at the support caused only by the
redundant reaction acting on the member.

15. Equilibrium
Draw a free-body diagram and write
appropriate equations of equilibrium
for member using calculated result for
redundant force.
Solve the equations for other
reactions

16. EXAMPLE
A-36 steel rod shown has diameter of 5 mm. It’s
attached to fixed wall at A, and before it is loaded,
there’s a gap between wall at B’ and rod of 1 mm.
Determine reactions at A and B’.

17. Compatibility
Consider support at B’ as redundant.
Use principle of superposition,
(+)
0.001 m = δP −δB
Equation 1

18. Compatibility
Deflections δP and δB are determined from Eqn. 4-2
PLAC
δP =
= … = 0.002037 m
AE
FB LAB
δB =
= … = 0.3056(10-6)FB
AE
Substituting into Equation 1, we get
0.001 m = 0.002037 m − 0.3056(10-6)FB
FB = 3.40(103) N = 3.40 kN

19. Equilibrium
From free-body diagram
+ Fx = 0;
− FA + 20 kN − 3.40 kN = 0
FA = 16.6 kN

20. THANK YOU