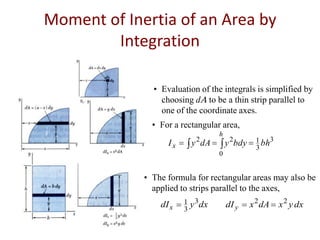
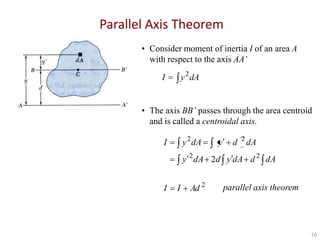
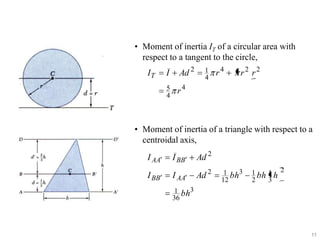
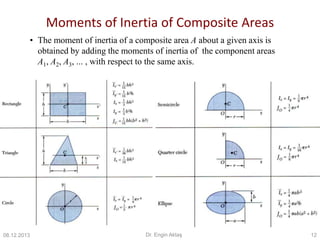
This document presents information on moments of inertia based on a course titled "pre-stressed concrete". It introduces moments of inertia and how they are calculated based on the distribution of mass or area relative to a given axis. Formulas are provided for calculating the moments of inertia of basic shapes like rectangles and circles through integration. The parallel axis theorem is also described, which relates the moments of inertia about different axes passing through an object. Examples are worked through, such as finding the moment of inertia of a triangle with respect to its base.

1. Welcome to presentation
Based on moment of inertia
Rafiqul islam
10.01.03.005
Course No: CE 416
Course Title :pre-stressed concrete

2. Introduction
• Forces which are proportional to the area or volume
over which they act but also vary linearly with
distance from a given axis.
- the magnitude of the resultant depends on the first
moment of the force distribution with respect to the
axis.
- The point of application of the resultant depends on
the second moment of the distribution with respect
to the axis.
Herein methods for computing the moments and
products of inertia for areas and masses will be
presented

3. The definition of moment of inertia is mathematical:
I
y 2 dA
where y is the distance of an element dA of an area
from an axis about which the moment of inertia is
desired. Generally,
The axis is in the plane of area , in which case it is
called a
rectangular moment of inertia.
The axis is perpendicular to the area, in which case
is called a polar moment of inertia.

4. Moment of Inertia of an Area

F
• Consider distributed forces
whose
magnitudes are proportional to the elemental
areas A on which they act and also vary
linearly with the distance of
from a given axis.
• Example: Consider a beam subjected to pure
bending. Internal forces vary linearly with
distance from the neutral axis which passes
through the section centroid.

F
ky A
R
k y dA 0
M
k y 2 dA
y dA Qx
first moment
y 2 dA second moment

5. Moment of Inertia of an Area by
Integration
• Evaluation of the integrals is simplified by
choosing d to be a thin strip parallel to
one of the coordinate axes.
• For a rectangular area,
Ix
2
h
y dA
y 2bdy
0
1 bh3
3
• The formula for rectangular areas may also be
applied to strips parallel to the axes,
dI x
1 y 3dx
3
dI y
x 2 dA
x 2 y dx

6. Polar Moment of Inertia
• The polar moment of inertia is an important
parameter in problems involving torsion of
cylindrical shafts and rotations of slabs.
J0
r 2 dA
• The polar moment of inertia is related to the
rectangular moments of inertia,
J0
r 2 dA
Iy
Ix
x2
y 2 dA
x 2 dA
y 2 dA

7. Radius of Gyration of an Area
• Consider area A with moment of inertia
Ix. Imagine that the area is
concentrated in a thin strip parallel to
the x axis with equivalent Ix.
Ix
2
I x kx A
kx
A
kx = radius of gyration with respect
to the x axis
• Similarly,
Iy
2
Iy ky A ky
A
JO
2
J O kO A kO
A
2
kO
2
kx
2
ky

8. Examples
SOLUTION:
•
• A differential strip parallel to the x axis is chosen for
dA.
dI x y 2dA
dA l dy
• For similar triangles,
Determine the moment of
inertia of a triangle with respect
to its base.
l
b
h
y
l
h
b
h
y
h
dA b
h
y
h
dy
• Integrating dIx from y = 0 to y = h,
Ix
h
2
y dA
2
y b
h
0
3
b y
h
h
3
y
h
dy
bh 2
hy
h0
y 3 dy
4 h
y
4
Ix
0
bh3
12
8

9. SOLUTION:
• An annular differential area element is chosen,
dJ O
u 2 dA
dA
r
JO
dJ O
2 u du
r
2
u 2 u du
2
0
0
JO
a) Determine the centroidal polar
moment of inertia of a circular
area by direct integration.
b) Using the result of part
a, determine the moment of
inertia of a circular area with
respect to a diameter.
u 3du
2
r4
• From symmetry, Ix = Iy,
JO
Ix
Iy
2I x
2
r4
2I x
I diameter
Ix
4
r4
9

10. Parallel Axis Theorem
• Consider moment of inertia I of an area A
with respect to the axis AA’
y 2 dA
I
• The axis BB’ passes through the area centroid
and is called a centroidal axis.
y 2 dA
I
y
d 2 dA
y 2 dA 2d y dA d 2 dA
I
I
Ad 2
parallel axis theorem
10

11. • Moment of inertia IT of a circular area with
respect to a tangent to the circle,
I
Ad 2
5
4
IT
r4
1
4
r4
r2 r2
• Moment of inertia of a triangle with respect to a
centroidal axis,
I AA
I BB
I BB
Ad 2
I AA
2
Ad
1 bh3
12
1 bh 1 h 2
2
3
1 bh3
36
11

12. Moments of Inertia of Composite Areas
• The moment of inertia of a composite area A about a given axis is
obtained by adding the moments of inertia of the component areas
A1, A2, A3, ... , with respect to the same axis.
08.12.2013
Dr. Engin Aktaş
12

13. Thanks to everybody