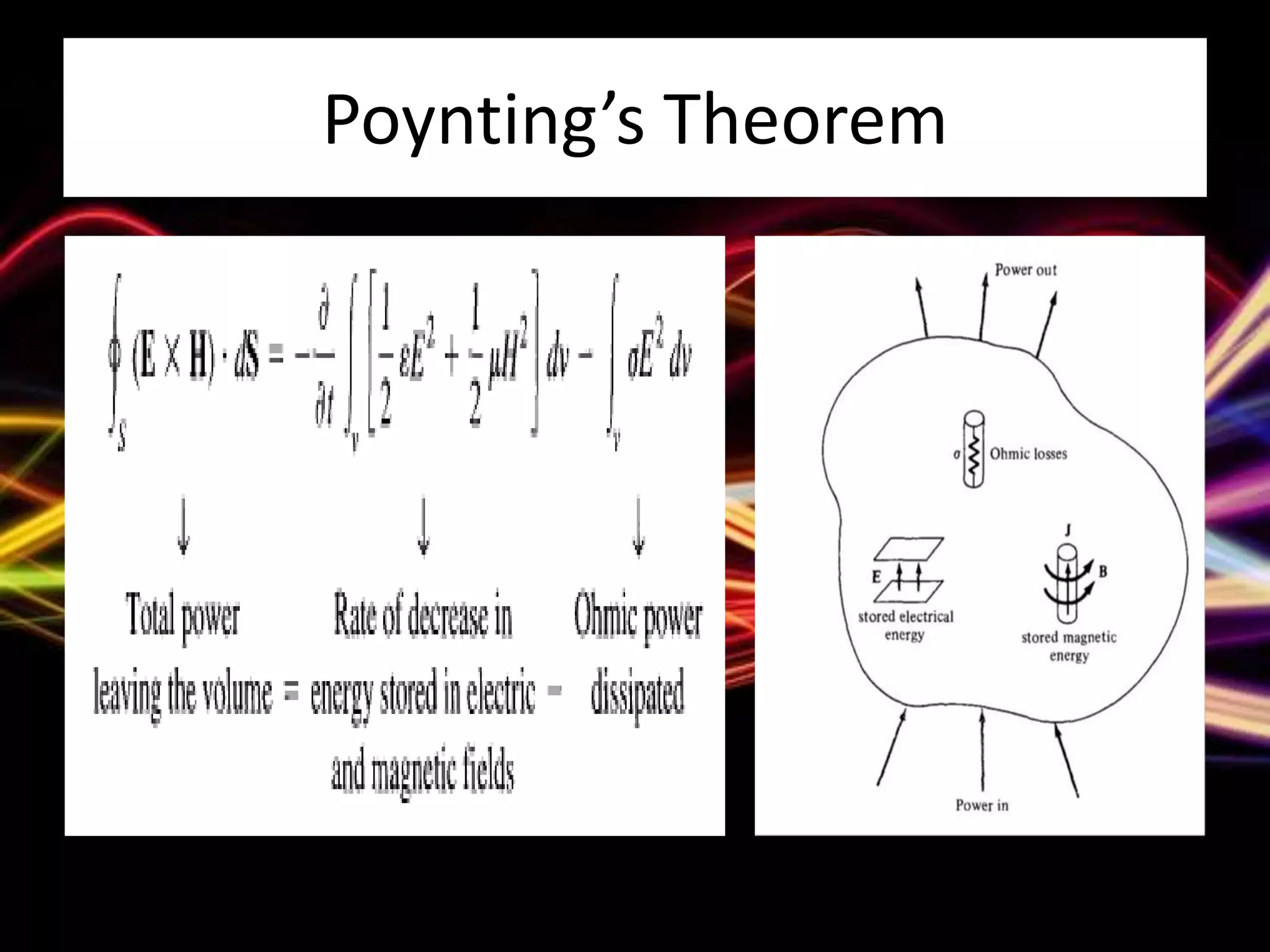
Poynting's theorem relates to the conservation of energy in electromagnetic fields, describing how energy transfer correlates with charge work via energy flux. The Poynting vector expresses the directional flow of energy, exemplified in applications such as coaxial cables and plane waves. Poisson's and Laplace's equations address potential fields from charge distributions, with criteria for unique solutions defined by boundary conditions.

1. ELECTROMAGNETIC THEORY

2. POYNTING’S THEOREM

3. Poynting’s Theorem
• Poynting's theorem is a
statement of
conservation of energy
for the electromagnetic
field, in the form of a
partial differential
equation, due to the
British physicist John
Henry Poynting.

4. Poynting’s Theorem
• Poynting's theorem is
analogous to the work-
energy theorem in classical
mechanics, and
mathematically similar to
the continuity equation,
because it relates the
energy stored in the
electromagnetic field to the
work done on a charge
distribution (i.e. an
electrically charged object),
through energy flux.
Continuity equation

5. Statement:
The rate of energy transfer (per unit volume) from a
region of space equals the rate of work done on a
charge distribution plus the energy flux leaving that
region.
Or
The decrease in the electromagnetic energy per
unit time in a certain volume is equal to the sum of
work done by the field forces and the net outward
flux per unit time"

6. Expression(general representation):
• ∇•S is the divergence of
the Poynting vector
(energy flow)
• J•E is the rate at which
the fields do work on a
charged object (J is the
current density
corresponding to the
motion of charge, E is
the electric field.
• u is the Energy Density

7. POYNTING THEOREM -
DERIVATION

8. Maxwell's Equations:
• Energy can be
transported from one
point (where a
transmitter is located)
to another point (with a
receiver) by means of
EM waves.
• The rate of such energy
transportation can be
obtained from
Maxwell's equations:

10. Poynting’s Theorem

11. POYNTING VECTOR

12. Poynting Vector
• The cross product E × H is known as the Poynting
vector, S,
• The direction of the vector S indicates the
direction of the instantaneous power flow at a
point
• Many of us think of the Poynting vector as a
“pointing” vector. This homonym, while
accidental, is correct.

13. Poynting Vector
• Because S is given by the cross product of E
and H, the direction of power flow at any
point is normal to both the E and H vectors.
• This certainly agrees with our experience with
the uniform plane wave, for propagation in
the +z direction was associated with an Ex and
Hy component,

14. Poynting Vector

15. Dipole radiation of a dipole vertically in the page showing electric field
strength (colour) and Poynting vector (arrows) in the plane of the page.

16. Across any plane P between the battery and resistor, the Poynting
flux is in the direction of the resistor. The magnitudes (lengths) of the
vectors are not shown accurately; only the directions are significant.

17. Poynting Theorem -
Applications

18. 1. Co-Axial Cable
• Poynting vector within the dielectric insulator of a
coaxial cable is nearly parallel to the wire axis
• Electrical energy delivered to the load is flowing
entirely through the dielectric between the conductors.
• Very little energy flows in the conductors themselves,
since the electric field strength is nearly zero.
• The energy flowing in the conductors flows radially into
the conductors and accounts for energy lost to resistive
heating of the conductor.
• No energy flows outside the cable, either, since there
the magnetic fields of inner and outer conductors
cancel to zero.

20. 2. Plane waves
• Propagating sinusoidal
linearly polarized
electromagnetic plane
wave of a fixed
frequency, the Poynting
vector always points in
the direction of
propagation while
oscillating in
magnitude.

21. 2. Plane waves
• The time-averaged magnitude of the Poynting
vector is
• Em is the complex amplitude of the electric
field and η is the characteristic impedance of
the transmission medium, or just η = 377Ω for
a plane wave in free space

22. 3. Radiation Pressure
• Radiation pressure is
the pressure exerted
upon any surface
exposed to
electromagnetic
radiation.
• c is the speed of light in
free space

23. 4. Static Fields
• Shows the relativistic
nature of the Maxwell
equations and allows a
better understanding of
the magnetic component
of the Lorentz force, q(v ×
B)
• Circulating energy flow
may seem nonsensical or
paradoxical, it is
necessary to maintain
conservation of
momentum.

24. POISSON’S AND LAPLACE’S
EQUATION

25. Poisson’s equation
• Poisson's equation is a partial differential
equation of elliptic type with broad utility in
mechanical engineering and theoretical
physics.
• It arises, for instance, to describe the potential
field caused by a given charge or mass density
distribution; with the potential field known,
one can then calculate gravitational or
electrostatic field.

26. Poisson’s equation
• For a homogeneous medium,
• Solving Poisson's equation for the potential
requires knowing the charge density
distribution
• It is a generalization of Laplace's equation

27. Laplace’s equation
• If the charge density is zero in Poisson’s
equation, then Laplace's equation results,
when pv = 0
• Laplace's equation is a second-order partial
differential equation named after Pierre-
Simon Laplace who first studied its properties

28. Laplace’s Equations

29. Boundary Conditions
• If the field exists in a region consisting of two
different media, the conditions that the field
must satisfy at the interface separating the
media are called boundary conditions.
• These conditions are helpful in determining
the field on one side of the boundary if the
field on the other side is known

30. UNIQUENESS THEOREM

31. Statement:
“If a solution of Laplace's equation can be found
that satisfies the boundary conditions, then the
solution is unique”
The theorem applies to any solution of Poisson's
or Laplace's equation in a given region or closed
surface.

32. UNIQUENESS THEOREM -
DERIVATION

35. Application
Before we begin to solve boundary-value problems,
we should bear in mind the three things that
uniquely describe a problem:
1. The appropriate differential equation (Laplace's or
Poisson's equation in this chapter)
2. The solution region
3. The prescribed boundary conditions
A problem does not have a unique solution and
cannot be solved completely if any of the three
items is missing.