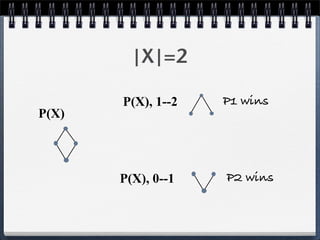
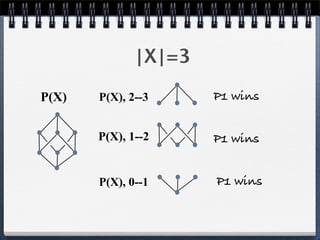
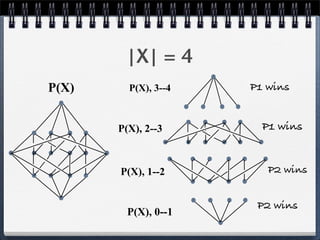
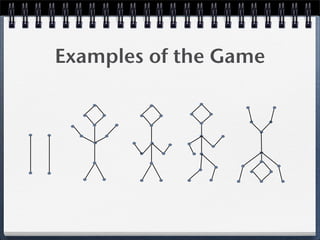
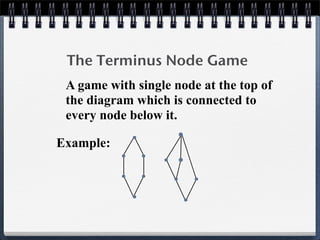
This document outlines several theorems about partial order games: 1. Theorem 1 proves that in a game with n stacks of height 1, Player 1 wins if n is even and Player 2 wins if n is odd. 2. Theorem 2 generalizes the game to include "lambdas" (upside-down Y shapes) and line segments, proving that Player 1 wins if the total number of lambdas and line segments plus the number of nodes is odd. 3. Theorem 3 proves that if a game has a "totally comparable point" connected to all other nodes, Player 1 has a winning strategy.

1. Partial Order Games
Davian Vernon
Leon John
Haile Russom
Under the supervision of Dr. Marshall Cohen

2. Outline
Introduction
Rules and examples
Theorem 1
Lambda game
Theorem 2
Terminus Node game
Theorem 3
Power Set games

3. Introduction
Definition: A Partially Ordered Set (Poset) is a set
with a relation “≤” satisfying
1. x ≤ x for all x  X ( Reflexive Property)
2. x ≤ y and y ≤ x implies x = y ( Anti-Symmetric)
3. x ≤ y , y ≤ z implies x ≤ z ( Transitive Property)

4. Example of Poset
x ≤ y
We draw a finite Poset in the plane with
x ≤ y connected by downward paths.
y
x

5. Rules of 2-Player Poset
Game
A Player can only remove one node per
move.
The player to remove the last Node Loses.
Note: When removing a node, everything
above it is taken as well.
y
x z z

6. Examples of the Game

7. Theorem 1
Given: n stacks of height 1
Thus:
If n is even then Player 1 (P1) wins
If n is odd then Player 2 (P2) wins
n

8. Proof of Theorem 1
P(n): Given n stacks of height 1, P1 wins when n is even and
P1 loses when n is odd.
Claim: Theorem is true for n stacks.
Base Step: n=1.
There is only 1 node present and P1 must remove it,
therefore P1 loses.

9. Inductive Hypothesis: Assume theorem is known for n-1
stacks.
Inductive Step: Assume P(n-1), show P(n) is true.
Case 1: Assume n is even → P1 moves. The remaining number
of stacks n-1 is odd → P1 wins by the inductive hypothesis
Case 2: Assume n is odd → P1 moves. The remaining number
of stacks n-1 is even → P1 loses by the inductive hypothesis
Proof of Theorem 1 cont.

10. The Lambda Game
We know that in the one node, n-stack game that
P1 will take the last node if n is odd and P2 will
take the last node if n is even.
Consider the addition of the following element:
Now we have the following game:

11. Conjecture 1
Suppose we have a graph of l ‘lambdas’ and n nodes,
where l ≥ 1 and n ≥ 0, then:
If l or n is odd then Player 1 will win.
If l and n are even then Player 2 will win.
l=1, n=5
l=2, n=0
P1 wins
P2 wins
Examples:

12. Lambdas & Lines
Consider:
*The addition of s line segments to the Lambda
game.
s

13. Conjecture 2
Thus we will have the following conjecture:
Suppose we have a graph of l ‘lambdas’, s segments
and n nodes, where l + s ≥ 1 and n ≥ 0, then:
If l + s or n is odd then Player 1 will win.
If l + s and n are even then Player 2 will win.
l+s=1, n=2
P1 wins
l+s=2, n=2
P2 wins

14. k-Segmented Lambdas
Using conjectures 1 and 2, we can adapt a theorem for a game
of n nodes and l lambdas containing k segments (treating line
segments s as single segmented lambdas).
Theorem:
Suppose we have a graph of l, k segmented ‘lambdas’ and n nodes,
where k, l ≥ 1 and n ≥ 0, then:
If l or n is odd then Player 1 will win.
If l and n are even then Player 2 will win.
.....
ln
K

15. Proof of Theorem 2
Base case: l = 1 (k segments)
P1 wins because:
- P1 removes a line segment if n and k are both
even or are both odd.
- P1 removes top node if n or k are odd.
n
.....K

16. Proof of Thm 2 cont.
Inductive Hypothesis: Assume we know the theorem holds for l-1:
- If l-1 or n is odd then P1 wins.
- If l-1 and n are even then P2 wins.
Inductive step: Show that this works for l
Case 1: l is odd. (Claim: P1 always wins.)
a. If n is odd then P1 removes line segment, destroying a ‘lambda’,
to leave P2 with l-1 ‘lambdas’ and n + 1 nodes, both n and l being even
b. If n is even then P1 removes a top node, destroying a ‘lambda’, to
leave P2 with l-1 ‘lambdas’ and n + 2 nodes, both being even.

17. Proof of Thm 2 cont.
Case 2: l is even.
- The first player to destroy a ‘lambda’ loses in this case so now
the players are going to be choosing from n. Therefore we must
revert back to Davian’s inductive proof of n nodes.
• If n is odd, P1 will take the last node in n leaving P2 to
destroy the first ‘lambda’ (P1 win)
• And if n even, P2 will take the last node in n leaving P1 to
destroy the first ‘lambda’ (P2 win)

18. The Terminus Node Game
A game with single node at the top of
the diagram which is connected to
every node below it.
Example:

19. Theorem 3
If a poset game has a Totally Comparable Point, call it
the TCP, z such that for all x, x ≥ z or z ≥ x and z is not
minimal, then there exists a winning strategy for player
1 (P1).
(B)
(M) o

20. Proof of Theorem 3
Assume there exist a strategy for (B). Show P1 wins (M).
Case 1:
- If P1 wins game (B), then P1 will use the same strategy.
The strategy will have the same result in (M) because the
TCP is comparable to each of the nodes above it so they
will be removed as well. Thus P1 wins.
Case 2:
- If P2 wins game (B), then P1 will remove the TCP,
leaving only game (B). Then, P1 will be the 2nd player in
the game (B). Thus, P1 wins.

21. Power Set Games
The Power Set is a fundamental example
of a partially ordered set:
• If X is a set, P(X) = Set of all subsets of X.
• : A B iff x  A implies x  B
(P(X), ) is a partially ordered set.

22. Some P(X) Diagrams
|X|= 0 |X|=1 |X|=2
|X|=3
|X|=4

23. Who will win the power set
games?
P1 will always win the Power Set Game if |X| ≠ 0
because of Theorem 3:
There exists a maximal element (TCP) of P(X)
--- namely X.

24. What next?
So we consider the sub-games of P(X), (k -- k+1)
which involves all subsets of X containing k or (k+1)
elements (0 ≤ k < |X|).
P({1,2,3}), 1 -- 2
{1} {2} {3}
{1,2} {1,3} {2,3} 2 - elements subsets
1 - elements subsets

25. |X|=2
P(X)
P(X), 1--2 P1 wins
P2 winsP(X), 0--1

26. |X|=3
P1 wins
P(X), 2--3
P(X), 1--2
P(X), 0--1
P1 wins
P1 wins
P(X)

27. Show P1 wins P(X), 1--2,
|X|=3
P(X), 1--2
a
P(X), 1--2
P1 removes: a
Thus P1 wins

28. |X| = 4
P(X), 3--4
P(X), 2--3
P(X), 1--2
P(X), 0--1
P(X) P1 wins
P1 wins
P2 wins
P2 wins

29. Concluding Conjecture
If |X| = 2n + 1,
then P1 wins all P(X), k -- k+1 games (0 ≤ k < 2n+1)
If |X| = 2n then:
• P1 wins all P(X), k -- k+1 games (n ≤ k < 2n)
• P1 wins all P(X), k -- k+1 games (0 ≤ k < n)

30. fin.