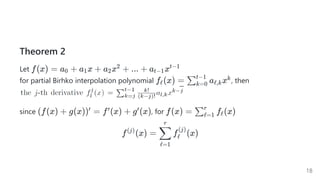The document introduces a dynamic and verifiable hierarchical secret sharing scheme designed to allow flexible management of shareholders and access conditions for secure vault operations. It outlines the mechanisms for adding, removing shareholders, and modifying access structures while ensuring perfect security and completeness. Key components include threshold signatures and Birkhoff interpolation for reconstructing the secret from shares held by authorized shareholders.

1. Dynamic and Verifiable Hierarchical Secret Sharing
ICITS 2016
Giulia Traverso, Denise Demirel, Johannes Buchmann
Technische Universität Darmstadt
林彥賓
2020/12/30

2. Outline
Introduction
Definition
Threshold Signatures
Feldman's VSS Protocol
Schnorr's ZK Protocol
Short Proofs Of Knowledge For Factoring
Multiplicative To Additive With Check Protocol
The Proposal Scheme

3. Introduction
the shares of the vault key may be distributed among bank employees
some of whom are tellers and some are department managers
The bank policy required 3 employees in opening the vault, but at least 1 of them
must be a department manager
3

4. Contribution
The first dynamic and veriable secret sharing scheme that is hierarchical, efficient, and
ideal with respect to the size of the shares
add and remove shareholders
modify the conditions for accessing the message, and to renew shares
4

5. Preliminaries
Secret sharing
message
shareholders where is the unique ID of shareholder
shares
access structure (partition of the set ) determines
authorized subset
unauthorized subsets
shareholders of a subset is denoted as
m
S = {s , ..., s }
1 n i ∈ I s ∈
i
S
σ , ..., σ ∈
1 n ∑
Γ ∈ P(S) S
A ⊂ S
U ⊂ S
R ⊂ S r := ∣R∣
5

6. secret sharing scheme
Share:
input: message
output: shares , where share is to be sent to shareholder , for
Reconstruct:
input: a set of shares held by a subset of shareholders
output: if , and otherwise
m
n σ , ..., σ
1 n σi si
i = 1, ..., n
σ , ..., sigma
1 r R ⊂ S
m R ∈ Γ ⊥
6

7. Definition
accessibility:
H(m∣σ(R)) = 0 ∀R ∈ Γ
perfect security: shares of unauthorized subsets do not reveal any
information about the value of the secret
H(m∣σ(U)) = H(m) ∀U ∈
/ Γ
Completeness: If the parties computing the shares and follow the algorithms
correctly, then each shareholder accepts the new share
Committing: If for any two authorized subsets and
, then if is the message reconstructed by the shareholders in ,
then
U ∈ S
A ⊂
1 S A ⊂
2 S, A , A ∈
1 2 Γ
mi A , i =
i {1, 2}
m =
1 m2 7

8. Dynamic Secret Sharing
Share:
input: a message
output: shares where share is to be sent to shareholder
, for
ADD:
input: set of shares held by a subset of shareholders and
the ID , of the new shareholder
output: If R is unauthorized, outputs . Otherwise, and without
message reconstruction, it outputs a corresponding share for the new
shareholder
m ∈ M
n σ , ..., σ ∈
1 n ∑
s ∈
i S i = 1, ..., n
σ , ..., σ
1 r R ⊂ S
i = n + 1
⊥ R ∈ Γ
σi
si
8

9. Reset:
input: a set of shares held by a subset of shareholders, a
new set of shareholders and an access structure
output: If is unauthorized, it outputs . Otherwise, and without
message reconstruction, it outputs shares where share sigma_i'
is to be sent to each new shareholder
Reconstruct:
input: a set of shares held by a subset of shareholders
outputs: if and otherwise.
σ , ..., σ
1 r R ⊂ S
S =
′
{s , ...s }
1
′
n′
′
Γ ⊂
′
P(S )
′
R ⊥ R ∈ Γ
n′ σ , ...σ
1
′
n′
′
s ∈
i
′ S′
σ , ..., σ
1 r R ⊂ S
m ∈ M R ∈ Γ ⊥
9

10. Secret Sharing Based on BirkhoInterpolation
(k, n)hierarchical threshold access structure
For disjoint levels be set of thresholds
Γ = {R ⊂ L : ∣R ∩ (∪ L )∣ ≥
h=0
ℓ
h t ∀h ∈
h {0, ..., ℓ} }
Example:
Let thresholds are namely, at least 7 participants, of whom
at least 4 are from , of whom at least 2 are from
L , ..., L , T
0 ℓ
T = (t , t , t ) =
0 1 2 (2, 4, 7)
L ∪
0 L1 L0
10

11. conjunctive secret sharing scheme
Share:
input: a message and generates a polynomial
outputs: shares , where share is to be sent to
shareholder , for and and is the -
th derivative of the polynomial
Reconstruct:
input: a set of shares held by a subset of shareholders
outputs: if , where is retrieved using Birkho interpolation. It
outputs otherwise
m f(x) = a +
0 a x +
1
a x +
2
2
... + a x , a :
t−1
t−1
0 = m
n σ ∈
i,j ∑ σ :
i,j = f (i)
j
s ∈
i,j Lh i = 1, ..., nh h = 0, ..., ℓ f (x)
j j
f(x)
R ⊂ S
m R ∈ Γ m = a0
⊥
11

12. Birkhointerpolation
problem of fnding a polynomial
satisfying the equalities , where is the ring of the polynomials
with degree at most
consider:
union of all shareholders from all levels constitutes the set of shareholders
S = {s , ..., s }, S =
1 n ∪ L
h=0
ℓ
h
threshold
f(x) = a +
0 a x +
1 a x +
2
2 ... + a x ∈
t−1
t−1 R [x]
t−1
f (i) =
j σi,j R [x]
t−1
t − 1
T = {t }
k k=0
m
12

13. share
input: message and generates a polynomial
where and the coecients are
chosen uniformly at random
outputs: shares is to be sent to shareholder , for
and is the level shareholder belong to
example
set , for shareholder
if will get the share
if will get the share , since
if will get the share , since
m f(x) = a +
0 a x +
1 a x +
2
2
... + a x
t−1
t−1
a :
0 = m a , k =
k 1, ..., t − 1
n σ =
i,j f (i)
(j)
s ∈
i,j Lh i =
1, ..., m, j = t , t =
h−1 −1 0 h i
T = (t , t , t ) =
0 1 2 (2, 4, 7) x
x ∈ L0 f(x)
x ∈ L1 f (x)
(2)
t =
0 2
x ∈ L2 f (x)
(4)
t =
1 4
13

14. Reconstruct
Define:
interpolation matrix matrix if shareholder
participates with share otherwise.
denoted by
set of function , and be the
-the derivative of
E : E = (e ) , e =
i,j i=1
r
j=0
ℓ
i,j 1 si,j
σ , e =
i,j i,j 0
I(E) = {(i, j) : e =
i,j 1} (i , j ), ..., (i , j )
1 1 r r
φ := {ϕ , ϕ , ϕ , ..., ϕ } =
0 1 2 t−1 {1, x, x , ..., x }
2 t ϕk
j
j k
14

15. Requirements for Birkhointerpolation matrices Intepolation
matrix should satisfy the following condition
Pólya's condition
no supported 1-sequences of odd length
1-sequence: a triplet of the form where ,
such that for all while
supported: there exist such that
E
(i, j , j )
0 1 1 ≤ i ≤ k, 0 ≤ j ≤
0 j ℓ
1
e =
i,j 1 j ≤
0 j ≤ j1 e =
i,j −1
0
e =
i,j +1
1
0
i
nw i i , j , j
sw nw sw j0 e =
i ,j
nw nw
e =
i ,j
sw sw 1 15

16. Set
16

17. Distributed Computation of Determinants
Theorem 1
for determinant of an matrix:
where results from by deleting the -th row and -th column
Let be the matrix that results from by removing the -
th row and the -th column
det(A) n × n
Ai,j A i j
A (E, X, φ)
ℓ−1,k A(E, X, φ) ℓ
(k + 1)
17

18. Theorem 2
Let
for partial Birhko interpolation polynomial , then
since , for
f (x) =
(j)
f (x)
ℓ=1
∑
r
ℓ
(j)
f(x) = a +
0 a x +
1 a x +
2
2
... + a x
t−1
t−1
f (x) =
ℓ a x
∑k=0
t−1
ℓ,k
k
(f(x) + g(x)) =
′ f (x) +
′ g (x)
′ f(x) = f (x)
∑ℓ=1
r
ℓ
18

19. Dynamic and Veriable Hierarchical Secret Sharing
Scheme
Share: The dealer
i. chooses two large primes
ii. set be a generator of the -th order subgroup of
iii. denfine and
are chosen uniformly at random
iv. compute commitments and broadcast
v. sends share to in private
vi. accepts as its valid share, if and only if
g ≡
σi,j
c =
k=j
∏
t−1
k
i
(k−j)!
k! k−j
g =
( i a )
∑k=j
t−1
(k−j)!
k! k−j
k
gf (i)
j
p, q, q∣(p − 1)
g q Fq Fp
∗
f(x) = a +
0 a x +
1 a +
x
2
... + a x , a =
t−1
t−1
0 m
(a , ..., a )
1 t−1
c =
k g mod
ak
p, k = 0, ..., t − 1
σi,j s ∈
i,j L , i =
h 1, ..., n , h =
h 0, ..., ℓ
si,j σi,j
19

20. Add: each shareholder performs
s ∈
ℓ R, ℓ = 1, ..., r
20

21. Reset: each old shareholder performs
i. computes its partial Birkhoff interpolation coecient
ii. chooses a polynomial
are chosen uniformly at random
iii. It computes subshare and send to shareholder in
private
iv. broadcasts commitment
v. It deletes its share
s ∈
ℓ R, ℓ = 1, ..., r
f (x) =
ℓ
′
a +
ℓ,0
′
a x +
ℓ,1
′
a x +
ℓ,2
′ 2
... +
a x , a , ..., a
ℓ,t −1
′
′ t −1
′
ℓ,1
′
ℓ,t −1
′
′
σ =
ℓ,i ,j
′ ′ f (i )
ℓ
′j′
′ si ,j
′ ′
′
c =
ℓ,k
′
g , c =
aℓ,k
′
0 gm
21

22. 22

23. Reconstruct: It takes as input shares held by a subset of shareholders.
If , it outputs reconstructed using Birkho interpolation.
otherwise output
Having access to , it is possible to verify whether the reconstructed
message is a correct opening value for commitment
R ⊂ S
R ∈ Γ m
⊥
c =
0 ga0
m c =
0 gm
23