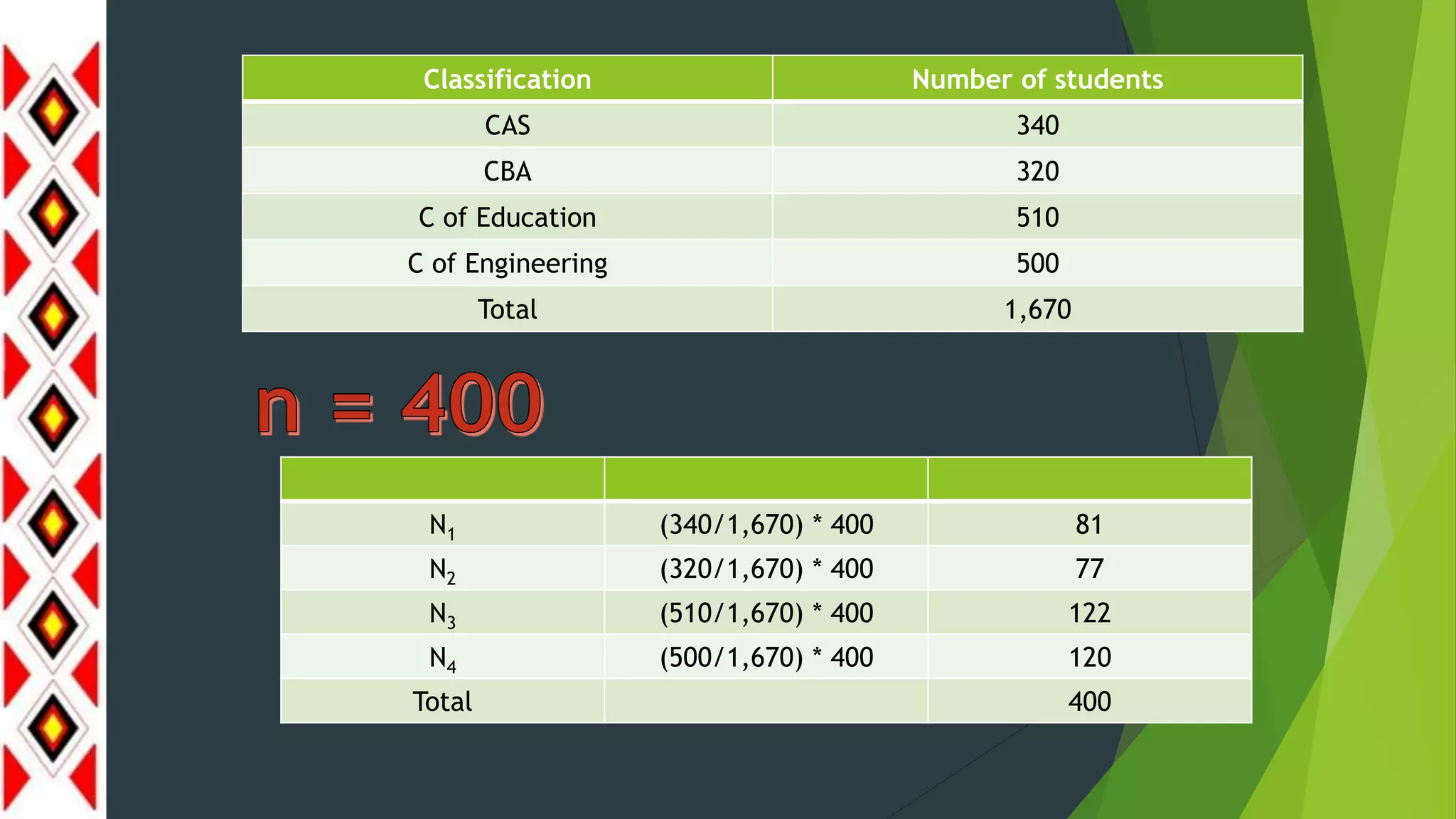
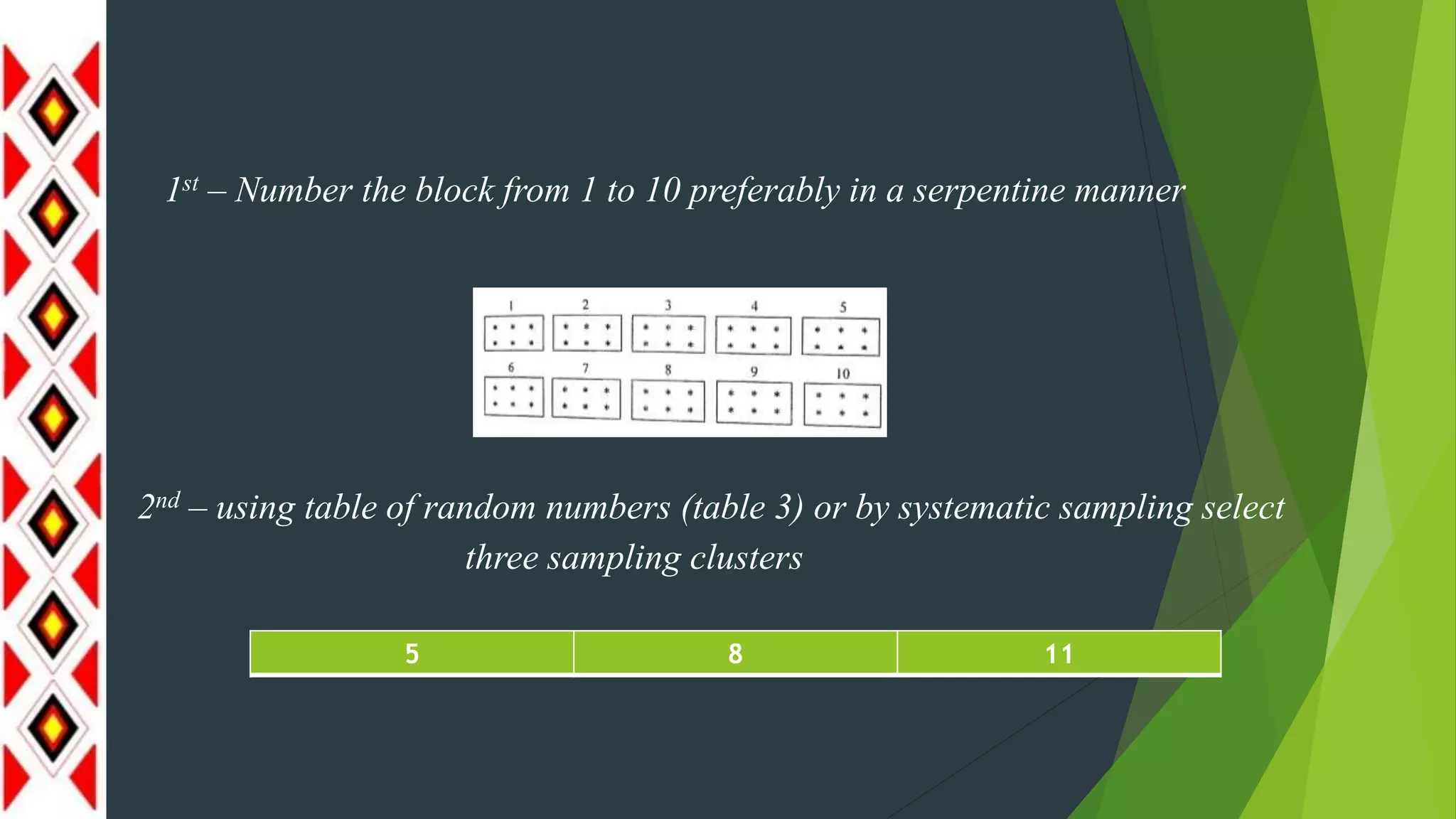
This document discusses population and sampling methods, specifically probability sampling. It defines key terms such as population, target population, and different sampling techniques like simple random, systematic, stratified, and cluster sampling. The text emphasizes the benefits of sampling, including reduced costs, greater speed, scope, and accuracy in research.

1. POPULATION AND SAMPLING
Part 1: Probability Sampling
EDGAR M. ANUD, JR.
MS – GENERAL SCIENCE EDUCATION
Republic of the Philippines
COLLEGE OF EDUCATION
Central Mindanao University
University Town, Musuan, Bukidnon

2. Population
 – is a well-defined set of elements or cases
whether individuals, animals, objects, or events
that conform to specific criteria and to which one
intend to generalize the results of the research
(McMillan,1998; Wood and Haber,1998).
 is a well-defined set of all cases of interest
(Shaughnessy et al.,2000).
Example: All teachers of DepEd; All Students in the Public School; All Albino
Carabaos of Mindanao; All Exotic medicinal plants of Bukidnon

3.  Finite population
- contains a countably limited number of
units.
 Infinite Population
- contains an endless number of
units.
Two types of Populations

4. Role of Population
 Topic population
> refers to the group or set about which generalizations will be made.
 Respondent population
>refers to the group or set who might be interviewed to obtain information
about a topic population.
Example: Suppose a researcher will undertake a study of the attitudes and values
of household heads towards overseas employment
ATTITUDES and VALUES
HEADS OF HOUSEHOLDS
 Target population
>is the group or set of items or individuals from which or about which
representative information is originally desired.
 Sampling population
>is the population from which a sample is actually drawn.

5.  Sampling refers to the processes whereby a sub-group
(called a sample) is picked out from a larger group
(referred to as population) and then use this sub-group as
a basis for making judgments about the larger group.
 Sample is a set of elements, or a single element from
which data are obtained (McMillan,1992).

6. Why Do Sampling?
Reduced Cost
Greater Speed
Greater Scope
Greater Accuracy

7. Probability Sampling
 Probability Sampling is based on the concept of random selection – a
controlled procedure that assumes that each population element is given a
chance to be included as a sample (Cooper and Emory, 1998).
Simple random sampling
Simple random sampling is a process of selecting a sample from
a set of all sampling units, giving each unit in the frame an
equal chance of being included in the sample.
Two ways of randomly selecting samples
1. Lottery or rifia
2. Use of Table of Random Numbers
- Prado et al., 2014

8. Systematic sampling
Systematic sampling refers to the process of selecting every kth
sampling unit of the population after the first sampling unit is
selected at random from the first k sampling.
Using the systematic sampling, how do you select six samples
from the total of twenty houses in a certain community?
1st – Number the houses 1 to 20
2nd – determine your sampling interval (k)
3rd – select your first sample at random
4th – add the selected first sample with the k

9. Stratified sampling
Stratified sampling involves during the population
into two or more strata and then taking either a
simple random (stratified random sampling) or a
systematic sample (stratified systematic sampling)
Proportionate allocation or Proportionate Stratified
Sampling
Sample Sizes for Proportional allocation (Walpole, 1982)
If we divide a population of size N into k strata of sizes N1 , N2… Nx
and select samples of n1, n2 … nk, respectively, from the k strata, the
allocation is proportional if
n1 = (N1/N) n, for I = 1,2,…, k, where n is the total size of the
statistical random sample.

10. Classification Number of students
CAS 340
CBA 320
C of Education 510
C of Engineering 500
Total 1,670
N1 (340/1,670) * 400 81
N2 (320/1,670) * 400 77
N3 (510/1,670) * 400 122
N4 (500/1,670) * 400 120
Total 400

11. Cluster Sampling
Cluster Sampling is a method of sampling a distinct of
clusters of smaller units called elements. A cluster refers
to any intact group of similar characteristics.
Scenario: Suppose the purpose of a study is to interview residents
of a rural community regarding their values and attitudes towards
employment. No list of residents is available but there is an
updated map of the community that is available. If the community
is divided into 10 blocks and we are to obtain a sample of 3 blocks,
how is it to be done using a cluster sampling?

12. 1st – Number the block from 1 to 10 preferably in a serpentine manner
2nd – using table of random numbers (table 3) or by systematic sampling select
three sampling clusters
5 8 11