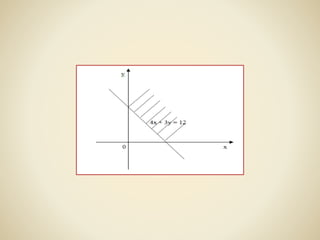
Dokumen tersebut membahas tentang persamaan dan pertidaksamaan linear satu variabel dan dua variabel. Secara ringkas, persamaan linear adalah persamaan yang hanya mengandung satu atau dua variabel pada derajat satu, sedangkan pertidaksamaan linear memiliki bentuk yang sama namun dengan tanda ketidaksamaan. Dokumen tersebut juga memberikan contoh-contoh soal dan penyelesaiannya.

1. Persamaan Linear dan Pertidaksamaan Linear
Disusun Oleh Kelompok : 4
Maysi Fatimah
Nur Afifah
Selvi Ernanti (190141629)

2.  Persamaan Linear Satu Variabel (PLSV)
Persamaan linier satu variabel adalah persamaan yang memuat satu variabel
berpangkat satu.
 Bentuk umum PLSV
Persamaan linear satu variabel mempunyai bentuk umum: ax + b = c dengan a = 0.
Penyelesaian PLSV adalah nilai yang memenuhi persamaan tersebut.
 Sifat-sifat PLSV
Sifat-sifat yang berlaku dalam PLSv adalah sebagai berikut:
1. Jika kedua ruas ditambah atau dikurangi dengan bilangan yang sama, diperoleh
persamaan yang ekuivalen.
2. Jika kedua ruas dikait atau dibagi dengan bilangan yang sama selain nol, diperoleh
persamaan yang ekuivalen.

3. Contoh PLSV;
Diketahui persamaan 5x + 2 = 17, tentukan nilai x!
Penyelesaian:
5x + 2 = 17
5x = 17 – 2 (pindahkan +2 ke ruas kanan menjadi -2)
5x = 15 (untuk mendapatkan nilai x, 15 dibagi dengan 5)
X = 3

4.  Persamaan Liner Dua Variabel
Persamaan linear dua variabel adalah persamaan yang mengandung dua variabel
dimana pangkat atau derajat satiap variabelnya sama dengan satu. Bentuk umum
persamaan linear dua variabel adalah:
a1x + b1y = c1
Dengan a, b, c ∈ R, a dan b tidak keduanya nol, dimana x, y: variabel real, a:
koefisien x, b: koefisien y, c: konstanta.

5. Contoh soal:
Jika (a, a + 7) merupakan penyelesaian persamaan 7x – 2y = -29, nilai a adalah...
Penyelesaian:
(a, a + 7) merupakan penyelesaian persamaan 7x – 2y = -29 sehingga x = a dan y =
a + 7 memenuhi peersamaan 7x – 2y = -29.
Subtitusikan x = a dan y = a + 7 ke dalam persamaan 7x – 2y = -29.
7x – 2y = -29
7 x a – 2 x (a + 7) = -29
7a – 2a – 14 = -29
5a = -15
a = -3

6.  Pertidaksamaan Linear Satu Variabel (PtLSV)
kalimat matematika yang memuat satu variabel berpangkat satu dan terdapat
tanda ketidaksamaan (>, <, ≤, ≥).
 Bentuk umum PtLSV
Persamaan linear satu variabel mempunyai bentuk umum:
o ax + b > c
o ax + b < c
o ax + b ≥ c
o ax + b ≤ c
o Dengan a = 0

7.  Sifat-sifat PtLSV
Sifat-sifat yang berlaku dalam PtLSV sebagai berikut:
1. Jika kedua ruas ditambah atau dikurangi dengan bilangan yang sama, tanda
ketidaksamaan tetap.
2. Jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama, tanda
ketidaksamaan tetap.
3. Jika kedua ruas dikali atau dibagi dengan bilangan negatif yang sama, tanda
ketidaksamaan dibalik.

8. Contoh PtLSV:
Carilah himpunan penyelesaian dari pertidaksamaan linier 3x – 6 > 0 !
Penyelesaian:
3x – 6 > 0 (pindahkan -6 ke ruas kanan menjadi +6)
3x > 6 (untuk mendapatkan nilai x, 6 dibagi dengan 3)
x > 2
Jadi, himpunan penyelesaiaannya, HP = {x | x > 2}

9.  Pertidaksamaan linear dua varuabel
Pertidaksamaan linear dua variabel adalah kalimat matematika yang memuat
Dua variabel berpangkat satu dan terdapat tanda ketidaksamaan (>, <, ≥, ≤
). Bentuk umum pertidaksamaan linear dua variabel adalah: ax + by > c
o ax + by < c
o ax + by ≥ c
o ax + by ≤ c
Dengan a,b : koefisien ( a ≠ 0, b ≠ 0, a, b ∈ R), c: konstanta (c ∈ R), x,y: variabel
real.

10. Contoh:
Tentukan daerah himpunan penyelesaian dari pertidaksamaan linear 4x + 3y ≥ 12
!
Penyelesaian :
a. Gambar garis 4x + 3y = 12 dengan cara menghubungkan titik potong garis di
sumbu x dan sumbu y.
b. Titik potong garis dengan sumbu x, y = 0, didapat x = 3 (titik (3,0))
c. Titik potong garis dengan sumbu y, x = 0, didapat y = 4 (titik (0,4))

11. Untuk menentukan daerah himpunan penyelesaian, maka harus dilakukan
pembuktian dengan cara mengambil titik uji pada salah satu sisi daerah. Sebagai
contoh, ambil titik (0,0).
Lalu substitusikan ke pertidaksamaan sehingga akan kita peroleh:
4x + 3y ≥ 12
4 x 0 + 3 x 0 ≥ 12
0 ≥ 12 (salah) , artinya tidak dipenuhi
Jadi, daerah penyelesaiannya yaitu daerah yang tidak masuk dalam titik (0,0).
Yakni daerah yang diarsir pada gambar di bawah ini:

13. Thanks You