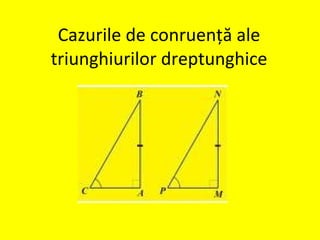
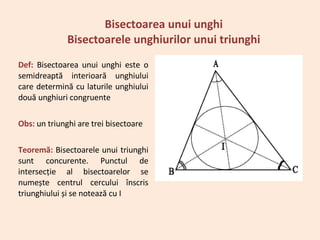
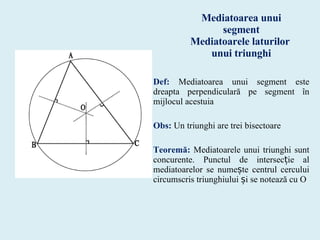
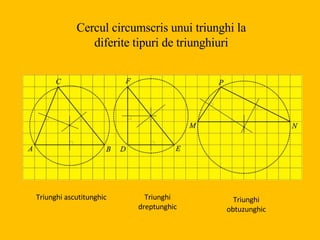
Documentul definește concepte fundamentale legate de perpendiculare și congruența triunghiurilor dreptunghice. Se discută despre bisectoarele și mediatoarele triunghiurilor, evidențiind proprietățile și teoremele asociate acestor elemente geometrice. În plus, se menționează criteriile de congruență pentru triunghiuri și relația dintre punctele de pe bisectoare și mediatoare.

1. Perpendicularitate

2. Def. : Doua drepte sunt perpendiculare daca determina un unghi drept. Not. : d 1 d 2 Def.: Prin distanta de la un punct la o dreapta se intelege distanta de la punct la piciorul perpendicularei din punct pe dreapta.

3. C a zurile de conruen ță ale triunghiurilor dreptunghice

4. Cazul C.C (cateta-cateta) : Doua triunghiuri dreptunghice care au catetele respectiv congruente sunt congruente. Cazul C.U. ( Cateta-unghi) : Doua triunghiuri dreptunghice ce au cate o cateta si unghiul ascutit respective congruente sunt congruente. Cazul I.U .(ipotenuza- unghi) : Daca doua triunghiuri dreptunghice au ipotenuza si unghiul ascutit respecttiv congruente sunt congruente. Cazul I.U. (ipotenuza-cateta) : Daca doua triunghiuri dreptunghice au ipotenuza si cate o cateta respective congruente sunt congruente.

5. Bisectoarea unui unghi Bisectoarele unghiurilor unui triunghi Def: Bisectoarea unui unghi este o semidreaptă interioară unghiului care determină cu laturile unghiului două unghiuri congruente Obs: un triunghi are trei bisectoare Teoremă: Bisectoarele unui triunghi sunt concurente. Punctul de intersecție al bisectoarelor se numește centrul cercului înscris triunghiului și se notează cu I

6. Mediatoarea unui segment Mediatoarele laturilor unui triunghi Def: Mediatoarea unui segment este dreapta perpendiculară pe segment în mijlocul acestuia Obs: Un triunghi are trei bisectoare Teoremă: Mediatoarele unui triunghi sunt concurente. Punctul de intersecție al mediatoarelor se numește centrul cercului circumscris triunghiului și se notează cu O

7. Triunghi ascutitunghic Triunghi dreptunghic Triunghi obtuzunghic Cercul circumscris unui triunghi la diferite tipuri de triunghiuri

8. Proprități ale punctelor de pe bisectoare și mediatoare Teorema1: Punctele de pe bisectoarea unui unghi se afla la aceeasi distanta fata de laturile unghiului. Teorema 2: Daca un punct situate in interiorul unghiului se afla la distante egale de laturile unghiului atunci el este situate pe bisectoarea unghiului. Teorema 3: Orice punct de pe mediatoarea unui segment este egal departat de capetele segmentului. Teorema 4: Orice punct egal dapartat de capetele unui segment se afla pe mediatoarea segmentului.